Centre de Physique Théorique - CNRS - Luminy, Case 907 F-13288 Marseille Cedex 9 - France
G. Cammarata
R. Coquereaux
We make a short review of the formalism that describes Higgs and Yang Mills fields as two particular cases of an appropriate generalization of the notion of connection. We also comment about the several variants of this formalism, their interest, the relations with noncommutative geometry, the existence (or lack of existence) of phenomenological predictions, the relation with Lie super-algebras etc.
anonymous ftp or gopher: cpt.univ-mrs.fr Keywords: Higgs, standard model, electroweak interactions, non commutative geometry
Work supported in part by a PROCOPE
project between Mainz University and CPT Marseille-Luminy.
Based in part on lectures given by R.C. at
the VI Simposio Argentino de Física Teórica de Particulas y
Campos, Bariloche (Argentina, January 95) and at the Schladming
Winter School (Austria, March 95)
CPT-95/P.3184
1. Introduction
This paper is written for those who are not willing to become experts in the field of noncommutative geometry but nevertheless want to understand the link between this approach and the usual formulation of the Standard Model of electro-weak interactions. The paper tries to give simple answers to the following questions:
The construction of
the full standard model (with usual quarks and leptons but also with
right neutrinos) is carried out by following the simplest possible
route (at least the simplest, from the point of view of the present
authors) and using an appropriate generalization of the notion of
connection. The present paper can be considered as a sequel of
[4] but can also be read independently; it should not be
considered as an expository lecture on the approach initiated by
[1].
2. The meaning of noncommutative geometry
From the point of view of Physics, one can summarize the situation very simply by saying that ``commutative geometry'' is the collection of mathematical tools describing classical physics whereas ``non commutative geometry'' is the collection of mathematical tools describing quantum physics.
Commutative geometry (or better ``commutative mathematics'') deals with mathematical properties of spaces (measurable, topological, differentiable, riemannian, homogeneous...). For the physicist, these "spaces" provide a mathematical model for the system under study and all the properties of interest can be expressed in terms of an appropriate class of (numerical) functions defined on such spaces. It is a fact - physically obvious but also mathematically rooted - that properties of "spaces" are entirely encoded in terms of properties of algebras of numerical functions (coordinates for example) or of objects themselves defined from numerical functions (forms, tensors etc.) The name ``commutative mathematics'' comes from the fact that a set of numerical functions defined on a space is a commutative (and associative) algebra for pointwise multiplication and addition of functions.
Non commutative geometry (or better ``non commutative mathematics'') deals with mathematical properties of algebras which are not necessarily commutative and generalizes - or tries to generalize - the constructions already known for commutative algebras (i.e. spaces) to non commutative situations (i.e. to operators).
This shows that one should maybe not always speak of ``commutative geometry'' or of ``non commutative geometry'' but of ``commutative mathematics'' or of ``non commutative mathematics''. What we have in mind in the present paper is not the use of non commutative mathematics in physics (because this could include, among many other things, the mathematics of quantum statistical mechanics) but non commutative differential geometry.
From an
epistemological point of view, and once the concepts of commutative
geometry and/or non commutative geometry have been mathematically
studied, one should probably revert the first general statement of
the present paragraph and define classical physics itself as a human
activity characterized by the wish of understanding what we call
"Nature" in terms of commutative mathematics and define quantum
physics in the same way but where the models are now expressed in
terms of non commutative mathematics. One could even go further and
declare that only the choice of the mathematical model (or models)
gives a meaning (meanings) to the whole thing (Nature) and that there
is no such thing as ``reality'' per se... but we now abandon these
philosophical considerations to return to the differential calculus,
commutative or not.
3. Non commutative versus commutative differential
calculus
A branch of non commutative differential geometry is non commutative
differential calculus. The aim is to be able to consider objects like
df or 
, i.e. differentials or covariant differentials,
and to perform computations with them, assuming that f is no longer
a function but an operator acting in some Hilbert space. Such a
calculus has been developed in the recent years. There exist several
kinds of non commutative differential calculi (for instance
[2, 3, 4, 5, 9, 10]) and we do not intend here to
describe them all. As a matter of fact, we shall describe none of
them. Indeed, it turns out that a very simple by-product of this
(these) generalization(s) gives us the necessary tools to understand
Higgs fields as generalization of connections (Yang Mills fields). In
some cases, for instance the 
model studied in
[4], this by-product actually belongs to the realm of
commutative geometry because it involves only commutative algebras of
functions on "spaces"! The point is that it was discovered
historically [1] only after the new developpements of non
commutative calculus. It is maybe a little bit misleading to call
"non commutative" some of these considerations, first because, in
simple cases, they are not so, and next because they give the reader
the feeling that he should first master all (or most of) the
niceties of non commutative differential calculus to understand the
constructions. Of course, this is a matter of taste and some people
could as well argue that one should always understand the general
before going to the particular...
4. Commutative non local differential calculus
In the previous paragraph, we said that the constructions that are at the root of our understanding of Higgs field as generalized connections do not really belong to the realm of non commutative differential geometry (they are a by-product). They however correspond to some commutative - but non local - geometry. Let us see why.
Consider a discrete set 
with two elements that
we call L and R. Call x the coordinate function 
and y the coordinate function 
. Notice that xy=yx=0, 
and x + y = 1
where 1 is the unit function 1(L)=1, 1(R)=1. An arbitrary element
of the associative (and commutative) algebra 
generated by
x and y can be written 
(where 
and
are two complex numbers) and can be represented as a diagonal
matrix 
. One can write 
and is isomorphic with 
. We
now introduce a differential 
satisfying 
,
and the usual Leibniz rule, along with formal symbols
and 
. It is clear that 
, the space of
differentials of degree 1 is generated by the two independent
quantities 
and 
. Indeed, the relation x+y=1
implies 
, the relations 
and 
imply 
, therefore 
and 
. This implies
also, for example 
,
, 
, 
etcMore generally, let us call
, the space of differentials of degree p; the above
relations imply that a base of this vector space is given by
. Call 
and 
. This space 
is an algebra: We can multiply forms freely
but one of course has to take into account the Leibniz rule, for
instance 
. Since each
is two dimensional we can easily represent it in terms of
matrices. More precisely, we can represent the element 
as the diagonal matrix
and the the element 
as the off diagonal
matrix 
In other words we
represent even forms by even (i.e. diagonal) matrices and odd forms
by odd (i.e. off diagonal) matrices; doing so is not only natural but
compulsory if we want the multiplication of matrices to be compatible
with the multiplication in . Indeed, the relations
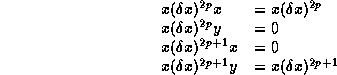
imply that the above
representation using 
matrices is indeed a homomorphism
of 
graded algebras from the algebra of universal forms
(graded by the parity of p) to the algebra of
complex matrices (with grading associated with the
decomposition of a matrix into diagonal and non diagonal components).
The presence of a factor i in the off diagonal matrices
representing odd elements (see above expressions) is necessary for
the matrix product to be compatible with the product in .
Notice that the algebra is infinite dimensional (since p
ranges from 0 to infinity) but if we represent the whole of
in terms of matrices acting on a fixed
2-dimensional vector space, the p grading is lost and only the
grading is left. The differential obeys the usual
Leibniz rule when it acts on elements of but a graded
Leibniz rule when it acts on elements of , namely
where 
denotes 0 or 1 depending if 
is even or
odd.
A one-form (this will be interpreted as a Higgs field and
can be seen to define a generalized connection) is an element of
. Take 
. The matrix representation of A reads therefore
The
corresponding curvature is then 
, but 
and 
, so that the
curvature can also be written
We now
chose a hermitian product on by declaring the base 
to be orthonormal. Then 
. One recognizes here a
(shifted) Higgs potential. The previous calculation (expressed in the
language of K-cycles) is already discussed in [1, 2] and
can be recognized in [4] where it is written in the language
of matrices.
The previous construction could of course be generalized. For
instance, we could take three points rather than two. It is easy to
show that in such a case, is of dimension 6 and
of dimension 12. If we take q points the dimension of
is 
. More generally, if we take infinitely many
points - take for instance points belonging to a manifold X - it
is easy to see that elements of can be defined as
functions A(x,y) of two variables on X such that A(x,x)=0 and
that elements of can be defined as functions F(x,y,z) of
three variables on X such that F(x,y,y) = F(x,x,y) = 0.
In
the case of the geometry on the discrete set - that is our
main example in the present paper - we recover the fact that an
element A of considered as a function of two variables
should satisfy the constraints A(L,L)=A(R,R)= 0 and can therefore
be written as off-diagonal matrices indexed by L and
R. An element F of considered as a function of three
variables should satisfy the constraints
F(L,L,R)=F(R,R,L)=F(L,R,R)=F(R,L,L)=F(R,R,R)=F(L,L,L)=0 so that non
zero components are F(L,R,L) and F(R,L,R). The fact that
for all p explains that we can use a
representation of fixed dimension (namely matrices) for
all values of p but one should maybe remember that it would not be
so if we were considering a geometry on more than 2 points.
Notice that we are here doing commutative differential calculus
(because the associative algebra of functions on a set of 2
elements is just the commutative algebra of diagonal 2 by 2
matrices with real or complex entries) but that we are doing a non
local differential calculus because the distance between the two
points labelled L and R can not be made infinitesimally small.
The reader will have recognized that one can interpret the above
results in terms of Higgs fields. This is the subject of our next
section.
5. What are the Higgses ? The Yukawa interaction term
Higgs fields ( 
) allow left and right fermions ( 
) to
communicate. In four dimensional Minkowski space, this is clear from
the trilinear Yukawa couplings such as 
that appear in the Lagrangian density of the Standard Model.
This should be contrasted with terms like 
or 
where 
or 
denote usual Yang Mills gauge fields. If we
had no Higgs fields, of course we would have no mass term but also no
possible communication (interaction) between right and left. There
would be no justification for choosing a single connected manifold to
modelize our universe. We would have a Minkowski space-time for the
right movers and a Minkowski space-time for the left movers.
Existence of chirality in four dimensions leads therefore to the
conclusion that we live in two parallel universes, one labelled by
L and the other by R. Usual connections - Yang Mills fields -
connect (infinitesimally) L and L together and R and R
together whereas Higgs fields are non local connections that connect
L and R and allow us to identify the two copies of our
universe.
As explained in all books of particle physics, the scalar interaction (Yukawa) of quarks is a priori of the form
where all quark fields of charge 2/3 are
collected into the multi-spinor field 
and
similarly for quarks of charge -1/3 with 
The
complex matrices 
and 
encode all
the dimensionless Yukawa coupling constants (here spinor and
scalar fields have their usual dimensions, namely 3/2 and 1 in
units of mass). If we expand the previous expression, we find
Let us now collect all left-handed quark fields (of charge
2/3 and -1/3) of the standard model into a single spinor 
and all right-handed quark fields into a single
spinor 
. Here 
and 
. The above Yukawa interaction term reads
where
The mass
term is obtained by shifting 
and 
by a
real constant with dimension of a mass that we call 
.
The mass term itself is therefore described by the mass matrix
Writing 
, the whole fermionic
lagrangian, for quarks, reads 
with
Where 
and 
collectively refer to those components
of the gauge fields coupled to the left and right handed sectors and
collectively refers as before to Higgs fields couplings. The
scalar interaction (Yukawa) of leptons is exactly of the same type.
The only possible difference is that, in the minimal Standard Model,
one does not usually add right neutrinos. We shall actually add such
right neutrinos: They will not be coupled to the gauge fields, of
course, but they will give a mass to the different kinds of Dirac
neutrinos and will be also coupled between themselves - via mass
matrices - and to the Higgses (and also therefore, in the unitary
gauge, to the longitudinal part of the gauge bosons). Notice that we
do not consider Majorana neutrinos. Introducing right neutrinos, not
only allows us to use the same formalism for quarks and leptons (the
only difference in the Yukawa interaction term is the replacement of
matrices and by 
and 
respectively) but also, as we shall see later, simplifies our
analysis. The Yukawa interaction for leptons is
where all leptons fields of charge -1
are collected into the multi-spinor field 
and
similarly for the neutrinos 
The
complex matrices and encode
all the Yukawa coupling constants. The whole fermionic lagrangian,
for leptons, reads as before, but with
In the standard model, one
should consider simultaneously not only the three generations of
leptons but also three copies (for color) of the three generations of
quarks. Taking into account - as above - the presence of three
kinds of right neutrinos, we get an interaction term 
, with 
and where both
and 
are multi-spinor fields - they are column
vectors with 24 components (since 24 = 3 + 3 + 3 (3 + 3)), each
component being itself a Weyl fermion.
In the spirit of
noncommutative geometry, one should think of 
as a
generalization of the Dirac operator (it incorporates masses and
Yukawa couplings) coupled to an algebraic connection. It should be
called the Dirac - Yukawa operator. The first piece in this
expression is a generalized differential operator since the mass
matrix 
appears as the inverse of a quantity encoding a
discrete set of fundamental lengths. The second piece is a
generalized connection: it incorporates both Yang-Mills and Higgs
fields.
6. The bosonic lagrangian
The theory of - usual - connections explains why 
is
the natural object (curvature) associated with a Yang-Mills field.
The root of the explanation being that the square of the corresponding
covariant differential is a linear object whose expression is
precisely given by the above formula. In the same way, and as
explained (section 4) in a very simple case, the theory of
generalized connections shows that 
is the natural object (curvature) associated
with the Higgs field introduced in the section 4 and
defined as a non local connection on the discrete set .
Now, we do not have a discrete set but a space 
that is the union of space-time for left-handed movers and
space-time for right-handed movers, in other words, we have the
product of Minkowski space by a discrete set of two elements called
L and R. The generalized curvature 
associated with the
generalized connection introduced in the previous
paragraph is
With
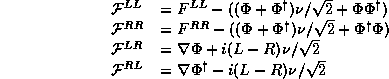
and
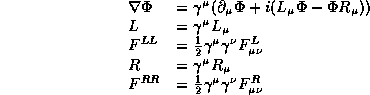
The symbols 
and 
denote the usual
curvatures of Yang-Mills fields associated with hermitian fields L
and R. The expression of matrix elements of given before
is a non trivial consequence of the formalism of non commutative
geometry (or of a non local commutative differential calculus!) and
can here be taken as a definition. These expressions can indeed be
computed from the theory of general connections (commutative or not).
The components of the curvature were obtained first by [1].
Up to different normalization factors and the presence of spurious
fields, their expression agrees with the one given just above. This
analysis was later improved in [2] (replacement of the
so-called algebra by 
). A detailed exposition of
the formalism of [2] using K-cycles and Dixmier trace can now
be found in several places [3, 17, 18]. The matrix
elements of given above were obtained by [4, 7] in
a simple way (and using the above notations). Our method is briefly
recalled in one of the ``comments'' of section 8.
Notice that the above expressions for have a dimension of
a mass squared and that, as a consequence, an arbitrary mass scale
appears in the formula. Explicitely, the term
and its
adjoint
can be computed from the expressions of given previously,
both in the quark and leptonic sectors.
Up to a normalization factors (we shall come back later to this
physically important problem) one recognizes that the trace of 
is nothing else than the lagrangian describing the
bosonic sector of the standard model: One obtains directly the
expression that usually comes after a shift by in the
Higgs fields and (see [4] for a
discussion of this point).
In a sense, the discussion could stop at this point. Indeed, we have seen in section 5 how to re-write the Dirac-Yukawa interaction term of fermions and in this section how to recover the whole bosonic sector of the Standard Model by treating Yang Mills fields together with Higgs fields as different components of a generalized connection. However, there are several claims made in the literature about possible constraints on the parameters of the lagrangian that one could obtain thanks to a formalism of non commutative geometry. Because we want to clarify this point (at least in the present formalism) we shall continue the discussion a little further.
The whole discussion comes actually from our understanding of the
notation 
that should denote a real number. From
the one hand, if we decide to introduce, by hand, as many arbitrary
constants in the expansion of this quantity (that gives rise to the
full bosonic lagrangian of the standard model) as gauge invariance
allows, we recover exactly the standard model with the same
(unpredictive) relations as usual, namely 
,
and 
where g, 
, 
and are undetermined.
If, on the other hand, we decide to introduce a 
constant 
in front of
in order to normalize simultaneously all the
gauge fields and Higgs fields, we obtain non trivial relations. The
interest of the formalism of non commutative differential geometry is
not, for us, tied up with the existence of such relations; it may be,
however,
that such relations turn out to acquire, some day, a better status.
For this reason, and also because the reader may be interested, we
shall devote the end of this section to discuss them.
After global multiplication by , we can rescale gauge fields
as usual by 
and also the Higgs fields by 
.
Under identification with the usual lagrangian one obtains
immediately 
; this relation is quite natural from a
point of view that identifies gauge fields and Yang Mills fields as
different components of a generalized connection. In that case, the
first general relation giving 
is not modified but the second
relation becomes
. Moreover, as we shall see below, the value of
also gets constrained.
Rather than writing again in full the well known bosonic lagrangian of the Standard Model, we shall examine several of the terms, as they appear here. First of all, notice that one can identify the two sides of
provided 
. The mass
value for the Higgs particle coming from this usual expression is
. Notice also that the left hand side
contains no additive constant (absence of cosmological term).
In our case, the Higgs potential itself coming from 
reads,
If we now express in terms of the component Higgs fields and
in terms of the matrices of Yukawa coupings then remove the factor
, in front, by rescaling the fields, we see that 
contains a term equal to 
but the term 
leads to a kinetic term
for 
equal to 
so that the mass of the Higgs
field does not depend on the mass of fermions and stays undetermined
(remember that is a free parameter). Other authors [18],
using a different formalism find quite stringent constraints
relating to the fermionic masses.
The full bosonic
interaction contains also a term 
; using the previous expression for 
implies
that the field L-R becomes massive, as it should. Indeed it
corresponds to the Z and W bosons. One may adopt the point of
view that the present formalism dictates a particular value for the
Weinberg angle; this value turns out to depend upon the fermionic
content of the theory. Indeed, the gauge fields L and R consist
of three copies of
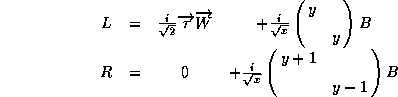
Here y = 1/3 for quarks since their weak
hypercharge is equal to
and y = 0 for leptons
since their weak hypercharge is equal to (y= - 1, y = - 1; y+1
= 0 , y-1= - 2) . We are introducing here right neutrinos that are
isospin singlets and for which y = 0.
For colourless quarks alone, the
normalization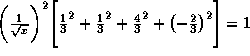 
would lead to x = 22 / 9 and 
For leptons alone, the normalization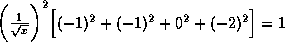 
would lead to x = 6 and 
More generally, if one uses an arbitrary representation and normalize fields L and R to 1 as above, one finds
which, in the case of three families of quarks (with
color) and leptons, gives 
(or 
as it is in the unified SU(5) theory. This would be therefore
the ``predicted'' value for the Weinberg angle. However, in the
usual approach, and even without SU(5) unification, one would
obtain exactly the same value by postulating that the gauge group is
not an arbitrary group isomorphic with 
but a group metrically isomorphic with the
subgroup of
SU(5). In absence of a principle based on the ideas of group
symmmetries (or a generalization of such a principle), one could
then ask on which grounds one should postulate such a property. The
same argument (or objection) holds here. Indeed gauge invariance
alone allows for the introduction of arbitrary constants in front of
the individual components of the gauge group. The conclusion is
therefore that, although the value appears quite
``naturally'' in this formalism, it should not be taken as an
unescapable consequence of the construction.
A last possible
``constraint'' concerns the mass of the W (or Z) particle.
Indeed, from the expression of we obtain a term 
that gives a mass to the
W and the Z. The trace itself reads
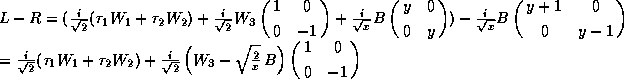
so
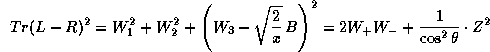
This gives the relation 
which is well known in the
standard model. In general, we have 
and this becomes only a constraint (namely 
) if we
set to the ``natural''
value 
as discussed before.
One could hope that such
relations could hold at a scale where the previous value for
is experimentally satisfied (maybe at some grand unification
scale). Notice that other authors [18], using a different
formalism (relying upon the choice of another differential algebra),
obtain another type of relations. Of course, we cannot (and will
not) pretend that other approaches should, or not, lead to the same
``numerical'' relations. Existence of constraints such as the above
ones can anyway be criticized since gauge invariance alone allows us
to multiply
terms of the bosonic lagrangian by arbitrary constants; this
possibility can be related to the choice of particular scalar
products in the space of forms [6]) and there are no
compelling reasons to set such constants equal to one (although it
may look quite natural in this formalism).
The main conclusion of this section is that the structure of the
whole bosonic lagrangian of the Standard Model can be obtained from
the formalism of non commutative geometry. Whether or not one should
look for constraints and take them seriously is another matter. Our
opinion is that, before reaching any conclusion on this line, one
should wait till we have a full understanding of the fully quantized
field theory in terms of non commutative geometry.
7. Higgs fields and super-algebras
The space where
lives is naturally graded by L and R, i.e.
can be decomposed into a left and a right part. Therefore
transformations that map fields to themselves fall naturally
into 2 kinds: those mapping L to L (and R to R) - we call
them ``even''- and those mapping L to R (and conversely) - we
call them ``odd''. Mathematically speaking, the space of these
transformations can be considered as an associative graded
matrix algebra whose corresponding Lie super-algebra is usually
denoted by GL(p|q) where p (resp. q) is the number of left Weyl
(resp. right) fermions entering the Lagrangian. The usual Yang-Mills
fields can be decomposed onto the even part whereas the Higgs fields
can be decomposed onto the odd part of this algebra. This is a rather
trivial remark since any Yang-Mills theory (and not only the Standard
Model) defined on an even dimensional space-time can be analysed
along the same lines. Another way to express the same idea is to say
that any Yang Mills theory with p left Weyl fermions and q right
Weyl fermions can be formulated in terms of representation theory of
some super Lie algebra posessing a representation on a graded
vector space of dimension p+q. In the case of the Standard Model
(with right neutrinos), and because all the fermionic species are
coupled to the same gauge and Higgs bosons, the matrix
describing this interaction can be decomposed on a subset of the
generators of 
. Since we have only 4 gauge bosons
and 4 Higgs bosons, we need only to use 8 generators (4 even
and 4 odd ones); in other words we only need to use (or to
recognize) the Lie superalgebra 
. The physical
representations of interest (namely leptons, quarks and possibly
right neutrinos) correspond to direct sums of Sl(2|1)
representations of dimension 3 = 2+1, 4 = 2+2 or 1. This fact
was actually observed long ago [28, 29] and sometimes perceived
as a kind of ``miracle''; for us, we consider this property as almost
tautological. The emergence of Lie superalgebras could lead people to
think that one should try to enlarge the formalism of gauge theory to
accomodate Lie superalgebras... Such attempts have been investigated
in the past and shown to lead to serious problems and have, in any
case, nothing to do with the Standard Model itself and even less with
the non commutative geometry presentation of the Standard Model. In
order to stress this point, let us consider the following analogy:
one can observe that Dirac spinors form a representation of the
Clifford algebra (the Dirac algebra of 
-matrices); this is
well known; as a consequence it is also true that the spinors with
four complex components also provide a representation for the (non
simple) Lie algebra generated by taking commutators of
arbitrary products of matrices; this does not mean that the
lagrangian of quantum electrodynamics should be invariant (globally
or locally) under such transformations. The fact that an algebra
(like the full algebra of matrices) is not directly related
with an invariance of the lagrangian does not make it useless (the
spin group and its Lie algebra can of course be expressed in terms of
the 's but the Clifford algebra itself is much bigger). Not
all algebras related to the mathematics of a physical model need to
describe ``invariances'' or ``symmetries''; the fact that they do
not does not make them useless!
The same thing is also true here for the super-algebra along the
representation of which one can decompose the matrices acting on the
vector space spanned by the multi-component spinor fields . This useful algebra is spanned by 8 generators.
The first four are matrices that, in the interaction term of the
lagrangian describing interaction between fermions and gauge bosons,
appear as coefficients of the Yang-Mills fields 
and B;
they are denoted, as usual, by 
and Y. The last four
are matrices that appear as coefficients of the Higgs fields 
and ; they give
rise (after having added the hermitian conjugate) to the Yukawa and
mass interaction term. We call them 
, 
,
and 
. More precisely, consider the
following (block) matrices:
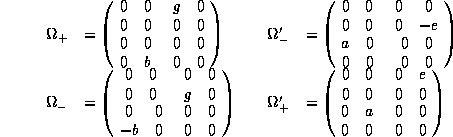
where a , b, g, e are themselves
square matrices, for example of size if we consider only
quarks coming in 3 families. In this case, we decide to label the
basis as follows:
.
Let us define 
,
and 
. The electric charge is 
Then, provided matrices
e,b,g,a satisfy the relation e b + g a = 1, one can show (it is
straightforward but cumbersome) that the matrices satisfy
the relations
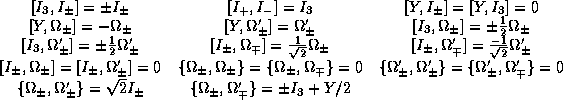
One recognizes
here the usual relations defining the Lie super algebra of
SL(2|1). In the case of quarks, one furthermore impose the
following constraints for the hypercharge generator: 
with 
,
and 
These constraints are satisfied if and only if, on top of the
relation 
, the matrices e,b,g,a satisfy also the
relations 
, 
and 
Indeed, one finds 
, 
and 
. This imply in particular g a = a g
and e b = b e.
One can then check that matrices 
and 
are then
automatically what they should be.
One may notice that the above expressions for Omega matrices
describing the gauge and Yukawa couplings of the quark family define
a Lie superalgebra representation which is equivalent to the sum of
(three) irreducible representations (each irreducible itself splits
into the direct sum of a doublet and two singlets under the branching
to the Lie algebra of 
).
Define now
and write 
This expression can not be real, indeed
would imply 
,
, but the other constraints would lead to a
contradiction ( 
). To obtain a real
expression, one has to add 
and 
.
Writing 
gives
and we recognize the expression of 
given in section 5,
with the identification 
and 
. Warning: The matrix 
defined previously in
terms of the matrices is not equal to the matrix
defined in section 5; in order to compare the two expressions, one
has to first add the conjugated expressions and . Taking into account the constraints on blocks a,g,e
and b, one obtains the relations: 
and 
These relations do not imply any ``new'' constraints on mass matrices
and since g and e are themselves
arbitrary. The main interest of those formulae is to provided a new
parametrisation for mass matrices or matrices of Yukawa couplings.
This could, in turn, suggest new phenomenological ansatz for them and
may even give us more insight into the structure of fermionic mass
matrices. Such an ansatz was analysed in [6] in the case of
two families and leads to a phenomenological expression of the
Cabibbo angle in terms of quark masses; another ansatz for matrices
a and b was analysed later in [14] for the case of three
families.
Remark: The quantity may be thought as the contribution to
the lagrangian of a particular representation of Sl(2|1). One can
think of as the contribution of the antiquark
representation to the lagrangian. However this identification is a
little bit tricky and may lead to possible mistakes of
interpretation; indeed, is not hermitian but is not the charge conjugate representation (in any case
weak interactions usualy violate charge conjugation and one should
not build a lagrangian that would be
C-even !). Given 
and 
as before,
one can define the following ``hatted'' matrices: 
and 
It is then straightforward to
check that these hatted matrices generate (thanks to the
same commutation relations) matrices 
, 
and 
, with, for example 
We obtain in this way
a new representation (the relation 
being automatically satisfied since 
).
With as before, we can rewrite as
and 
as
so that itself appears as the
contribution associated with the ``hatted'' representation. If one
wishes to use
in terms of a contribution of antiparticles,
for instance 
as 
, one can do it,
modulo proper care, but it may be misleading.
For leptons, the idea is the same as for the quarks and, in order to
straigthen even more the analogy, we add right neutrinos to the
Standard Model (they will turn out to be iso-singlets, as they should
be). We shall order the basis as follows:
with 
,
and
define matrices Omega as previously, in terms of new
block matrices e,b,g,a. However, in the case of leptons, the
constraints for the hypercharge generator are different. Indeed, 
with 
,
and 
These constraints are satisfied if
and only if, on top of the relation (which ensures
that commutation relations for SL(2|1) hold), the matrices
e,b,g,a satisfy also the relations 
and ag = 0. With
these constraints, one can then check that matrices ,
and Y defined as before in terms of the matrices are then
automatically what they should be.
One may notice that the above expressions for Omega matrices
describing the gauge and Yukawa couplings of the lepton family
(including right neutrinos) define a Lie superalgebra representation
which is equivalent to the sum of (three) reducible indecomposable
representations (each of them splits into the direct sum of a
doublet, a singlet, and the trivial representation under the
branching to the Lie algebra of ).
Again, we define
and write This expression can not be real, and, in
order to obtain a real expression, one has to add, as before, and . Writing gives
We recognize the expression of given in section 5, with the
identification 
and 
but the matrices a,g,e and b are not totally
arbitrary since they should here satisfy the constraints
and a g = 0. These relations do not imply any constraints on mass
matrices and but provided a new
parametrisation for them. This parametrization in terms of a,g,e,g
may, in turn, suggest new phenomenological ansatz (for instance one
can see what happens if these matrices a,g,e,g have particularly
simple forms). Such ansatz should then be considered as educated
guesses but not as ''predictions''.
Before ending this section, we would like to notice that
there exists still another interesting family of parametrizations for
matrices a,g,e and b. The reader can indeed check that, if we
chose arbitrary ( ) matrices 
and
choose a,g,e and b in such a way that 
,
, 
and 
, then, all commutation relations for
matrices are still satisfied. The generators 
and 
obtained from them are also equal to what they should be. However,
the obtained hypercharge generator Y is not diagonal (and not
necessarily hermitian) but equal to 
. In other words, this
describes a family of quarks-like objects which are not eigenstates
of hypercharge (hence of charge). The Lie superalgebra specialist may
relate this possibility to the existence of reducible indecomposable
representations of SL(2|1) whith non diagonal Cartan subalgebra
[15] (take nilpotent matrices).
Relation between family mixing and existence of such representations
was suggested in [6] but was leading to difficulties
(emergence of flavour changing neutral currents in the quark sector)
that could only be cured by a rather ad hoc treatment of the
definition of charge conjugacy. Here, we just notice that, after
having defined and as before and added the (usual)
complex conjugate, one obtain a real expression and one can choose to
diagonalize simultaneously and Y. The rotated quark-like
objects become now hypercharge (and charge) eigenstates, but the
values of their charges are not standard and deviate from their usual
values by corrections encoded in matrices . This
last family of parametrization leads therefore to something that
deviates from the Standard Model and we shall not elaborate more on
this topic.
The -graded algebra discussed in this section is
not usually mentionned in textbooks explaining the construction of
the Standard Model. However, if one decides to rewrite the lagrangian
in terms of multicomponent spinor fields
gathering all left and right fermionic species in this way, this
algebra (or better representations of it) appears naturally. It
plays a role very similar to the (Clifford) Dirac algebra itself. We
suggest to call it the ``Yukawa algebra''. Again, one should not
consider this algebra as a ``symmetry'' of the model and it is
probably better to avoid the word ``symmetry'' in this context in
order to avoid possible misunderstandings.
8. Comments
of universal forms. He then introduced [2] one of its
quotients, called it 
and used it in the sequel; this
approach was followed in particular by [17, 18, 19, 24]. In
[9, 13] a differential algebra 
was built
from A-valued derivations of the algebra A and subsequently used
in various papers [10, 11, 12].
The formalism of A. Connes is very general and should be able to
handle many problems of differential calculus in non commutative
geometry. The formalism proposed in [4] is not that general,
but if the purpose is to consider Yang-Mills fields and Higgs fields
as different components of the same mathematical object (an algebraic
connection), and to recover the lagrangian of the standard model in a
very simple way, this formalism is sufficient and does not require
any mathematics beyond an elementary knowledge of 
matrices. The remark at the origin of [4, 6, 7] is that it is
not necessary to use a 
-graded differential algebra to perform
the analysis. The situation is similar to what happens with ordinary
differential forms: one studies usually the theory of connections
(Yang-Mills fields) and covariant derivatives in terms of (usual)
differential forms like 
; however, in order to write a
lagrangian describing the interactions with spinor fields, it is
enough to represent these forms (in particular Yang Mills potential
and curvature) in terms of matrices like 
(which build a -graded algebra). The same thing is true here:
rather than using a -graded algebra of generalized differential
forms, we only use its representation on the graded vector
spanned by left and right spinor fields. This is why we only use
graded algebras in [4] (not graded ones). We
find this approach more familiar to physicists, and rich enough to
illustrate the idea of considering Higgs fields as gauge bosons
associated with the gauging of discrete directions (namely the jump
between left and right chiralities).
- actually
the Dirac-Yukawa operator- acting on a Hilbert space 
,
together with an associative algebra describing ``space''
and also acting on . In the case of a pure abelian theory,
would just be equal to the algebra of complex functions
on space-time. Actually, the formalism of [1] takes space-time
as euclidean and the Lorentz signature is recovered only at the end,
thanks to a Wick rotation.
In the case of a theory with symmetry breaking,
is equal to the direct sum of two algebras of complex
functions on space-time (one his labelled by ``left'' and the other
by ``right''); this algebra is still commutative and can be written
as the space of diagonal matrices with entries that are
functions on space-time. In a more complicated setting where the
gauge group is not abelian, one has just to replace the previous
by its tensor product with an appropriate matrix algebra.
In the second step one has to construct a differential algebra
(whose definition relies on the choice of ) out
of which one defines the generalized connections and curvatures. The
third step is the construction of the Yang-Mills (or generalized
Yang-Mills) Lagrangian itself and involves the so-called Dixmier
trace as a substitute for integration. The triple 
is called a K-cycle or a spectral triple. The formalism presented
in [4] starts with the same Dirac-Yukawa operator but does
not require the construction of the algebra and the use of
the Dixmier trace. Its clear advantage is simplicity but it is
lacking the character of generality expressed in [2, 3].
The only quantity to be computed is the expression for the
generalized curvature in terms of the generalized
connection , but this can be done once and for all. is not unique (all possible
choices can ultimately seen as quotients of a so-called ``universal''
one). The choice used by A.Connes in [1] is not the same as
the choice made by the same author in [2] and none of them
coincide either with the differential algebra introduced by
[9] or with ours. The choice described in [5] is a
differential algebra 
equal to the tensor product of usual
differential forms times the differential algebra built in section 4
for the space with 2 elements . One takes as
1-form and, using an appropriate d-operator defines as
the 2-form 
. The expression
previously given at the beginning of section 6 is nothing else that
the representation of in the fermionic space. The
calculations can be done very simply at the representation level
(this is recalled in section 8) and this why we skip the discussion
concerning the actual choice of the graded differential
algebra. Our point of view is that this freedom in the choice of the
differential algebra does not matter (in the case of the physical
system studied here) because all such choices lead essentially
to the same result, namely to the expression of similar to
the one given in section 6 and to the usual lagrangian of the
standard model. ``Essentially'' means that all the results
agree, up to factors of normalization. For instance, the expression
of the Higgs potential is exactly the same but the overall
coefficient may change. For instance, in the Connes' approach (where
one has to divide by ``junk forms'' to obtain ),
the kinetic term 
is proportional to
tr 
whereas the Higgs potential is proportional to
tr 
, with 
where M is a fermionic mass matrix. This potential vanishes whenever
is proportional to the unit matrix. In our case,
this was not so (see section 6). The coefficients appearing in front
of the kinetic term for scalar fields and of the Yukawa potential
depend upon the specific choice of the differential algebra. Spaces
, 
and 
for 
have been computed in [2] and it happens that
(when 
) they are respectively isomorphic, as
vector spaces, to the 
, 
and 
described in
[5] but the algebraic structure differs. More generally, the
structure of , when A is an arbitrary tensor product of
algebras was investigated in [20, 16, 22]. Introducing an extra
arbitrary constant in front of the whole potential amounts to
disregard possible mass relations. In such a case the several
approaches become completely equivalent, as far as physics and the
standard model of electroweak interactions are concerned. -grading matters). The
whole -graded differential algebra of universal forms
is therefore mapped onto an algebra that can be taken as the
-graded tensor product of the usual algebra of differential forms
times another graded differential algebra built in terms of
even dimensional square matrices. Here we forget about the
-grading of forms and remember only their parity, or
equivalently, we represent forms by using matrices belonging
to the Clifford algebra. The product is 
where a is a 
matrix and B is a form.
The differential is 
If we take as in section
5 and define 
,
we obtain the curvature given at the beginning of section
6. The reader should consult [4] for a simple exposition of
this calculation. It is not necessary to use the formalism of Lie
super algebras to obtain these results but one may also very well
choose to use it.
The definition and calculation of and in the
Connes' formalism is given in [2, 3, 17].
. This is not unique
and it can be seen that different choices for it amount to choose
different minima for the Higgs potential (see [4]). matrix the two
Higgs doublets coupling the left fermionic doublets to the fermionic
right and left singlets. Discarding Yukawa coupling constants we have
One
recognizes here a quaternion. Indeed, using Pauli matrices
, set 
, 
,
, then 
and 
. Moreover
This expression can
obviously be identified with .
Our next comment concerns stability by renormalization. It has been
shown [25] that some proposed constraints among masses of
particles of the standard model may not be stable with respect to the
renormalization group. This comment should be properly understood
and maybe taken with a grain of salt. Indeed, the free parameters of
the standard model are... free. Therefore one can renormalize them at
will (at a given scale) and one can, in particular renormalize them
in such a way that any relation between them is satisfied. Of course
it is absolutely true that a renormalization prescription involves
the choice of a scale (this ``substraction point'' is usually chosen
equal to some value of 
where q is a four-momentum) and that a
numerical relation between renormalized parameters may be deformed by
a change of scale if the relation is not invariant under the
renormalization group. But this fact does not mean that the relation
itself is physically meaningless. For example, the relation 
which is valid in the on shell
renormalization scheme of quantum electrodynamics can be imposed and
is actually imposed (because it is experimenally true on shell).
However this last relation is not invariant under the renormalization
group equations of QED! The third and last comment to be made about
these problems of relations between constants of the standard model
was already made in the text (section 6) but we repeat it here.
Descriptions of the Standard Model based on non commutative geometry
supplemented by the choice of specific scalar products in the space
of fields seem to lead, at the classical level, to relations between
the - otherwise arbitrary - constants of the model. Gauge
invariance alone allows for more freedom; in absence of a full
description of (spontaneously broken) quantum gauge field theories
in terms of non commutative geometry, such constraints should be
considered, in our opinion, as educated guesses. The reader may
refer to [18, 19] for a detailed analysis of these constraints
in the Conne's framework. For us, the true power of the non
commutative geometry desription of the standard model (and of
quantum physics in general) is not tied up with the relevance of
such constraints.
In its simplest ``version'', the standard
model does not incorporate right neutrinos. From the point of view of
non commutative geometry and if one restricts oneself to the leptonic
sector (take for instance the example of one family), lacking right
neutrinos is a little bit of a nuisance. Indeed, in such a case, and
in the language of A.Connes [1], the bundle of leptonic
species is non trivial and one needs to introduce a projector in the
formalism, projector whose curvature itself enters the final
expression. In the formalism explained in [4], the same
phenomena appears because our approach (based on the tensorization of
two by two complex matrices by arbitrary ones) leads to even
dimensional square matrices. In order to accomodate an odd number of
Weyl fermions (for instance 
and 
) one has to embedd
the odd dimensional matrix describing the connection into a even
dimensional one by adding line an columns of zeros. But then action
of the d operator creates non zero entries in such places. The
curvature is then not equal to but to 
where p projects on the odd dimensional subspace
spanned by the Weyl fermions. The result is, as it should, the usual
standard model without right neutrinos. However, introducing right
neutrinos in the game (like in [6] and like in section 5 of
the present paper) simplifies considerably the formalism because one
does not have to introduce such a projector. One cannot not say that
``Non commutative geometry predicts that the neutrino has a mass''
but it is clear that, from our perspective, the formalism is much
simpler with a right neutrino than without. Let us remind the reader
that such neutrinos are absolutely compatible with present
experimental data since the 
that one introduces for each
family is not coupled to the (transverse part of the) gauge fields.
Its main interest is to give a mass to the corresponding particle
(hence a Dirac spinor) and to introduce mixing between fermionic
families via a fermionic analogue of the Kobayashi-Maskawa matrix.
Introduction of right neutrinos in the Connes' formalism was recently
investigated in [26].
differential algebra. Of course this algebra is also
graded since forms are even or odd but generalized Yang Mills
potentials are defined here as one-forms and not only as odd forms.
The same is true in our case, see the discussion in [5].
Notice that when the differential algebra is represented on the space
of spinors, the grading is lost and only the grading is
left. Contrarily to what happens in the standard model, where the
generalized gauge field incorporates only Higgs and usual spin one
gauge fields, an algebraic super connection would also incorporate
other kinds of fields. Of course, one can consider a connection as
some kind of ``truncated'' super connection, but such a terminology
becomes then pointless and can bring confusion.
, the 6 quarks masses, the 6 leptonic
masses, the 
parameters of the leptonic and quark
mixing matrices, the mass of the W and the mass of the Higgs). We
shall stop here these numerological remarks and suggest the reader
interested in the beautiful properties of the number 24 to dive
into almost any book of arithmetics, modular function theory or
higher dimensional cristallography. ? Such a possibility is by no means ruled out but has not
been proven yet. If true, such a property would pave the way to the
next (ultimate?) goal of non commutative geometry (as far as physics
of electroweak interactions are concerned): a non perturbative
formulation of a fully quantized gauge field theory. The completion
of such an ambitious program would really be a truely non commutative
achievement.
and that the square of the corresponding generalized curvature gives
us the bosonic lagrangian of the standard model. This unification is
a little bit like the unification of electric and magnetic fields
taken as independent components of the Faraday tensor F. By itself,
such a unification is not a new theory in the sense that it was
``already there''. After all one can very well work with
electromagnetism without using a manifestly covariant formalism!
Also, it does not bring necessarily any new numerical prediction.
However, a unification of that kind is important at the conceptual
level. Moreover it usually leads to generalizations or to new ideas
that could be hardly thought of in a less unified framework.
Unification of Higgs and Yang-Mills fields is, for us the most
important success of non commutative differential geometry in
physics. This success is certainly going to stay.
Acknowledgments
We would like to thank our friends and
colleagues at C.P.T. (in particular G. Esposito Farese) and at the
University of Mainz (in particular R. Haussling and F. Scheck) for
many discussions on those topics. One of us (R.C.) wants to thank the
Erwin Schrodinger Institute, in Vienna, for its support and
hospitality.