We denote by the space of (graded) derivations on Gr(N), i.e. the analogue of the space of vector fields on . Calling a chart in Gr(N) we notice that is a left Gr(N)-module (actually a free module) and that is a basis of the module In other word, an arbitrary element of can be written with As a vector space, has a basis where I is a multi-index (with possible values) and and it is also a graded vector space: , with . Notice that, in particular, is odd.
In the classical (commutative) case the space of vector fields is not only a A(N)-module but also a Lie algebra. Here the situation is analogous: is a Lie superalgebra for the bracket and, in particular
We denote by the dual of on Gr(N) and denote by the elements of defined by in particular An arbitrary element of is an arbitrary linear combination of the . For an arbitrary element , one defines the d operator as Notice that is also a left Gr(N)-module. is also a graded vector space and we define . Notice that this definition of the grading makes the 's even as we shall discuss it now.
We now call the space of Gr(N)-valued, graded alternate Gr(N)-linear k-forms over Notice that . Elements of can be multiplied and becomes the Grassmann analogue of the usual algebra of exterior forms in . This space can also be considered as the exterior algebra over but the wedge product between 1-forms is now symmetric. Actually this is quite natural: 1-forms anti-commute in commutative geometry but they commute in anti-commutative geometry! In other words (and in practice) it is enough to remember that d is odd, as well as the 's so that is even and we can use the usual Milnor'sign rule. To avoid confusion, we denote this product `' in the sequel, and write for instance There is a only one d operator of square 0 that extends the d of the one-forms to the whole of and this space becomes then a -graded and bigraded differential algebra (the bigrading is with respect to ). Indeed, an arbitrary element of can be written where is a covariant (down indices) symmetric tensor with coefficients in Gr(N), therefore where is a multi index. Each single term of this last sum is of the kind and this is why we have an -bigrading (k,p). Because of the commutativity between the themselves, graded commutativity of the wedge product depends only the grading . One can also introduce an interior product and a Lie derivative in but we shall not use those concepts and we refer to [8] and [4] for more details. What is important for us is that ; therefore, employing the above notation we can write with
![]()
and
![]()
where the symbols denote complete symmetrization and where
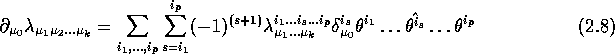
As usual, the hat on means that this factor has been omitted in the product. Notice that because of the symmetry properties of the product, the family is a generating family for vectors, but is not a basis of , unless we impose an ordering constraint like (this is analogous to the situation prevailing in the case of usual exterior forms).
At the dual level, currents - that we take as p-vectors - will also be represented by contravariant (up-indices) symmetric tensors with coefficients in Gr(N), i.e. The pairing between p-vectors and p-forms is given by
![]()
A well known result of elementary tensorial calculus (or of quantum mechanics of systems with identical bosonic particles) tells us that the space of symmetric tensors of order p built on a vector space of dimension N has dimension , but in the present case, the coefficients belong to the Grassmann algebra Gr(N), itself of dimension , therefore the space of differential forms over Gr(N) has dimension Notice that, in contrast with the case of usual exterior forms over or over a finite dimensional manifold, the space of all such forms (direct sum of all spaces for all values of p) is infinite dimensional since grows with p.
The pairing between contravariant and covariant symmetric Gr(N)-valued tensors (i.e. currents and forms) enables one to define a boundary operator already mentioned before. Writing for a p-vector and a (p-1)-form leads to
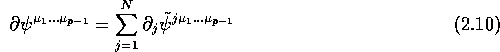
where `` '' denotes the involution of Gr(N) associated with the grading, i.e. a change of sign in front of odd monomials (for instance if then ).
Notice that a Gr(N)-valued contravariant tensor defines a Gr(N)-valued differential operator of degree p, namely where the product of symbols is now just the composition law as , is identically zero when is symmetric. In what follow, we will use p-vectors with a symmetric wedge product . Differential operators and p-vector coincide only when p=1. In that case, the quantity , which is the boundary of can also be called the (graded) divergence of the operator with, of course, This identification is used, for instance in [3].
The last thing to study in this paragraph is the Grassmann analogue of De Rham cohomology of differential forms (or Grassmann homology of currents). Let us denote by , and One can prove that this cohomology is trivial: Indeed one can construct (see for instance [4]) an operator h from to such that d h + h d = 1, therefore, given a closed form , one defines and shows that is exact () by using the previous relation between d and h. From this point of view, Grassmann algebras are topologically trivial (as their ``commutative''counterpart): The Poincaré lemma holds.
Before ending this paragraph, let us remark that the symbol appearing in the Berezin integral should not be considered as a shorthand for , at least not with the symmetric product , as defined above, in mind. Indeed the law of change of variables in the Berezin integral shows that this integral should be transformed by a global -1 multiplicative constant upon a parity-odd change of chart such that
![]()
and this is clearly incompatible with a symmetric wedge product. One possibility is to introduce a new (antisymmetric) product - that one would call ``.'' rather than ``''- between the 's, just for the sake of making the notation compatible with the law of change of variables. Another possibility is to refrain from writing a Grassmannian volume element in Berezin integrals, but this notation is now quite popular Let us only remember that the ``natural'' product between 's is the symmetric one and that it is that one that we have been using and shall use in the following, even if we do not write explicitly the wedge symbol. Actually, Berezin himself, in his book [7] does not use the symbols in his integrals but the symbol and warns the reader (footnote page 76) that he should confuse the with the differential : it is his notation that we have chosen, and we will write for the volume element:
![]()