Let 
be the Grassmann algebra over 
with two generators,
i.e. the linear span of 
with arbitrary complex
coefficients, where the generators satisfy the relations 
and 
. This algebra has an even part,
generated by 1 and 
and an odd part generated by 
and
.
We call 
the algebra of 
matrices over the complex numbers and
another copy of this algebra that we grade as follows: A matrix 
is called even if it is of the type
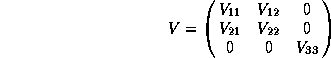
and odd if it is of the type
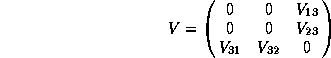
We call 
the Grassmann envelope of which is
defined as the even part of the
tensor product of and , i.e. the space of matrices matrices V with entries 
, 
, 
, 
, 
,
that are even Grassmann elements (of the kind 
) and entries 
, 
, 
, 
that are odd Grassmann elements (i.e. of the kind 
).
We define 
as
Explicitly,
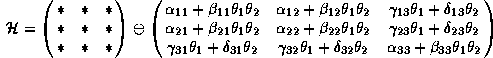
All entries besides the 
's are complex numbers (the above
sign is a direct sum sign: these matrices are 
matrices written as a direct sum of two blocks of size ).
It is obvious that this is an associative algebra, with usual matrix
multiplication, of dimension 27 (just count the number of arbitrary
parameters). is not semi-simple (because of the appearance of
Grassmann numbers in the entries of the matrices) and its semi-simple
part 
, given by the direct sum of its block-diagonal
-independent parts is equal to the 9+4+1= 14-dimensional
algebra 
. The
radical (more precisely the Jacobson radical) J of is
the left-over piece that contains all the Grassmann entries, and only
the Grassmann entries, so that
. J has therefore dimension 13.