References

1

A. Alekseev, D. Gluschenkov and A. Lyakhovskaya, Regular representation of the quantum group 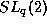(q is a root of unity), St. Petersburg Math. J., Vol 6, N5, p 88-114 (1994)

2

D. Arnaudon, Fusion Rules and R-matrices for representations of 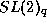at roots of unity, hep-th/9203011

3

V.Chari, A.Pressley, A guide to Quantum Groups, Cambridge University Press (1994)

4

A. Connes NonCommutative Geometry and Reality, IHES/M/95/52

5

A. Connes, Gravity coupled with matter and foundation of non-commutative geometry, hep-th/9603053

6

A. Connes and A. Chamseddine, The spectral action principle, hep-th 9606001

7

R. Coquereaux, G. Esposito-Farese and G. Vaillant, Higgs fields as Yang-Mills fields and discrete symmetries, Nucl. Phys. B353, 689 (1991).

8

R. Coquereaux, G. Esposito-Farese and F. Scheck, An SU(2|1) theory of electroweak interactions described by algebraic superconnections, Int. Jour. of Mod. Phys. A, Vol. 7, No 26 (1992) 6555-6593

9

R. Coquereaux, R. Haussling and F. Scheck, Algebraic connections on parallel universes, Int. Jour. of Mod. Phys. A, Vol. 10, No 1 (1995) 89-98

10

R. Coquereaux, O. Ogievetsky. Comments on the properties of finite dimensional Hopf algebras related with 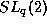when q is a primitive root of unity, CPT-Preprint. To appear.

11

E. Corrigan, D. Fairlie, P. Fletcher and R. Sasaki, Some aspects of quantum groups and supergroups, J. Math. Phys. 31, 776 (1990)

12

C.W. Curtis, Modular Lie Algebras. I, Transac. of the Amer. Math. Soc., Vol 82 p 161-179 (1956)

13

C.W. Curtis, Representation of Lie algebras of classical type with applications to linear groups, J. Math. Mech. 9, 307-326 (1960)

14

P. Di Francesco and J.-B. Zuber, in Recent Developments in Conformal Field Theories, Trieste Conference, 1989, S. Randjbar-Daemi, E. Sezgin and J.-B. Zuber eds., World Scientific 1990

15

M. Dubois Violette, Derivations et calcul differentiel non commutatif, C.R.A.S. Paris, 307, Série I (1988), 403-408

16

M. Dubois Violette Non-commutative differential geometry, quantum mechanics and gauge theory, in Differential Geometric Methods in Theoretical Physics, Rapallo 1990 (C. Bartocci, U. Bruzzo,, R. Cianci, eds), Lecture Notes in Physics 375, Springer-Verlag 1991.

17

D.V. Gluschenkov, A.V. Lyakhovskaya, Regular representation of the quantum Heisenberg double (q is a root of unity), Zapiski LOMI 215 (1994).

18

N. Jacobson, Abstract Derivation and Lie algebra, Transac. of the Amer. Math. Soc., Vol 42 p 206-224 (1937)

19

N. Jacobson, Restricted Lie algebras of characteristic p, Transac. of the Amer. Math. Soc., Vol 50 p 15-26 (1941)

20

G. Lusztig, Finite dimensional Hopf algebras arising from quantized universal enveloping algebras, J. of the Amer. Math. Soc., Vol 3, N1, p 257-296 (1990)

21

G. Lusztig, Quantum groups at roots of 1, Geometrica Dedicata,Vol 35, p 89-114 (1990)

22

H.Ewen, O. Ogievetsky and J. Wess, Quantum matrices in two dimensions, Letters in Math. Phys. 22, 297-305, 1991

23

O. Ogievetsky and J. Wess Relations between 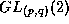's, Z. Phys. C - Particles and Fields 50,123,131 (1991)

24

M. Marcu, The representations of spl(2|1), J.Math. Phys. 21(6) 1277-1283 (1980)

25

C.P. Martin, J. Gracia Bondia and J. Varilly, The Standard Model as a noncommutative geometry: the low mass regime, hep-th/9605001

26

Y. Ne'eman, J. Thierry-Mieg, Anomaly-free sequential superunification, Phys. Lett. B108 (1982) 399-402

27

A. Ocneanu, private communication. See also: Paths on Coxeter diagrams, from Platonic solids and singularities to minimal models and subfactors (notes recorded by S. Goto, Univ. of Tokyo (in Japanese))

28

O. Ogievetsky, Matrix structure of 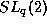when q is a root of unity. CPT-96/P3390

29

V. Pasquier and H. Saleur, Common structure between finite systems and conformal field theories through quantum groups, Nucl. Phys. B330 (1990) 523

30

R. Suter, Modules over 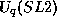, Comm. in Math. Phys., Vol 163, p 359-393 (1994)

31

S. Vokos, J. Wess and B. Zumino, Analysis of the basic matrix representation of 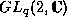, Z. Phys. C48, 65 (1990)