Let q be a primitive cubic root of unity ( 
). Hence,
and 
. We also set 
. In order to write generators for , we need to
consider 
matrices that have a 
block diagonal structure. We introduce elementary
matrices 
for the 
part and elementary matrices
for the 
part.
The associative algebra defined previously can be
generated by the following three matrices
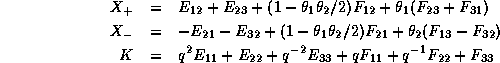
Explicitly, one gets
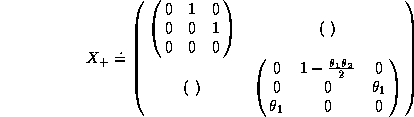
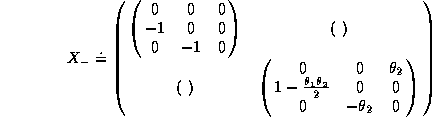
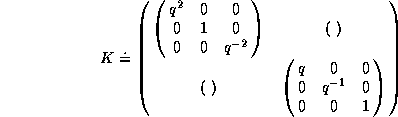
Performing explicit matrix multiplications or using the relations 
, 
and
,
it is easy to see that the following relations are satisfied:
It is relatively easy and straightforward to check that the following 
matrices 
are linearly independent and span as vector space over 
.
This shows that the matrices 
generate as an algebra.
It is instructive to write these generators in terms of Gell Mann matrices, Pauli matrices and SU(2) doublets :
Let 
denote the Gell Mann matrices (a
basis for the Lie algebra of SU(3)) and 
denote the Pauli matrices (a basis for the Lie algebra of SU(2)).
Since we have to use matrices, we call 
, 
. Therefore
,
and we set
. We shall also
need the SU(2) doublets
and
One can then rewrite the generators 
and K as follows:
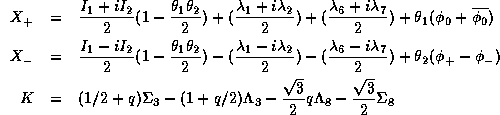
Before ending this subsection, we want to note that the matrix
(use
)
commutes with all elements of . If we set 
,
and let h go
to zero (which of course cannot be done when q is a root of unity !),
the expression of C formally coincides with the usual Casimir operator.
The explicit expression of C reads
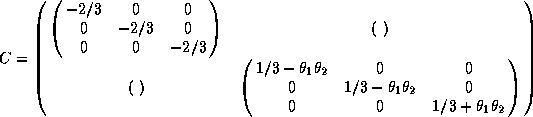
This operator, when acting by left multiplication on the algebra,
has two eigenvalues (-2/3 and 1/3) and we see explicitly that the
eigenspace 
associated with eigenvalue -2/3 is isomorphic with the 9
dimensional space 
whereas the eigenspace 
associated with eigenvalue 1/3
consists only of nilpotent elements
and coincides with the 13-dimensional radical J already
described. In other words, we have 
and 
. We obtain in this way another decomposition of as
the direct sum of subspaces of dimension 9, 13 and 5 (the
supplement).
It is useful to consider the following matrix: 
because its square projects on the block of
. The projector is
.
In the same way, it is useful to consider a matrix that projects on
the 
block of . One can use 
.
This matrix is not a projector but it nevertheless does the required
job since it kills the elements of the upper left block. Indeed,
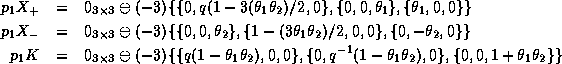
The above properties show that 
.
These two matrices 
and 
are very useful since they allow
us to express any element of in terms of the generators
and K (something that is for instance needed, if one wants to
calculate the expression of the coproduct --see below-- for an arbitrary element of
, since the coproduct is usually defined on the generators).
One can express in this way the 27 elementary matrices (with or without 
's)
For illustration only, we give :
and
.