The fact that , defined in this way, admits a non trivial Hopf algebra
structure --in particular a coproduct-- is absolutely not obvious at first sight.
Let us remind the reader that it is the existence of a coproduct
that makes possible to consider tensor products of
representations, exactly as it were a finite group. This is obviously of
prime importance if one
has in mind to find some physical interpretation for and consider
``many body systems'' (or bound states). For instance, in the case of the
rotation group, if 
denotes the third component of angular momentum,
the coproduct reads 
and
this tells us how to calculate the third component of the total angular
momentum for a system described by the tensor product of two Hilbert
spaces, namely 
.
We now define directly the coproducts, antipode and counit in .
,
,
,
.
,
,
,
.
As usual, the square of the antipode is an automorphism (and it is,
in this case, a conjugacy by 
, i.e. 
).
is defined by
,
,
,
,
.
Notice that the resulting Hopf algebra is neither commutative nor
cocommutative.
We now have to check that all expected properties are indeed satisfied.
Here are the main required properties for a Hopf algebra (we do not list the
usual algebras axioms involving only the multiplication map
and we do not list either the
axioms involving the antipode).
where 
exchanges the second and third factors in
.
The reader may check, in an elementary way, that all these properties
are indeed satisfied, either by
using the above generators and relations or by using the explicit presentation of
given before and explicitly performing the tensor products of matrices.
For illustration only, we check co-associativity on the generator 
.
We first compute
We then compute
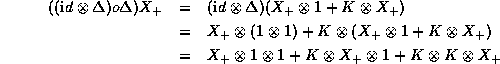
Both expressions are indeed equal.
To illustrate the non triviality of this result (the existence of a Hopf
structure on ), let us mention,
for instance, that the algebra 
does not even carry any
Hopf structure at all (it is known that the only semi-simple Hopf algebra
of dimension 5 is the commutative group algebra defined by
the cyclic group on five letters). In our case, the presence of the
part is crucial: although can be written as a direct
sum of two algebras, namely of and of 
, the
coproduct mixes non trivially the two factors. If one wants to use this
algebra (or another non co-commutative Hopf algebra) to characterize
``symmetries'' of some physical system --for instance in elementary
particle physics-- one should keep in mind that, in contrast with
what is done usually in the case of symmetries described by Lie
algebras, the ``quantum numbers'' will not
usually be additive.
Our explicit description of the algebra allows one to
compute explicitly the coproduct of an arbitrarily chosen element in
.
One has first to express the chosen element in terms of the
generators 
and K (for that, one may use 
and 
).
What is then left to do is a simple calculation
using the fundamental property of 
, namely that it is a
homomorphism of algebras : 
for U and V in .
Warning: With the notations given at the end of section 3, we see that, for
example, 
, however 
is not
equal to 
, etcIn order to appreciate the rather non trivial mixing induced by the
coproduct, we give -- part of -- the expression 
(recall that
is an elementary matrix of ``color type'', i.e. 
,
containing only a 1 in position (1,1). We have re-expressed the
result in terms of elementary matrices 
--of color type-- and
--of electroweak type.
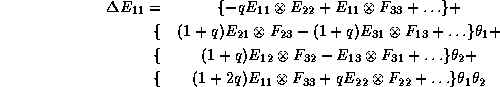
What is important in this example is not the expression itself (!) but
the fact that it involves the and the . In a
sense, one can generate a coupling to the 
part by building ``bound states'' from the ``color part'' alone.
We can also compute the expression of
the coproduct for a generator of ``electroweak type'',
like 
with 
and 
.
A rather long -- but straightforward -- calculation leads (for a two
body system, i.e. 
to a rather lengthy result for 
. The main feature is that
this ``charge'' is not additive : 
is not
equal to 
and, moreover, it couples non trivially
the 
part together with the 
part.