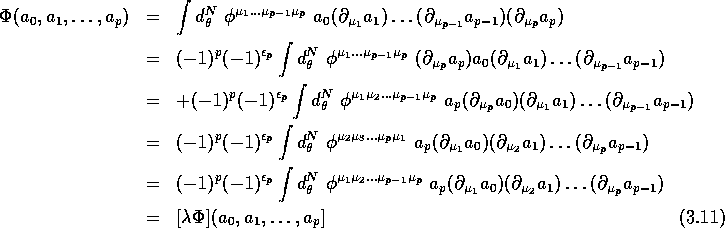
We already showed that a closed current of degree p (or a closed p-vectors) can be written in terms of a divergence-free differential operator of degree p, i.e. in terms of a Grassmann valued contravariant symmetric tensor satisfying It remains to show that it defines a cyclic cocycle . We already know (because it is a current) that it defines a Hochschild cocycle. The only thing to check is that it is cyclic. The following sequence of equalities establishes the claimed property.
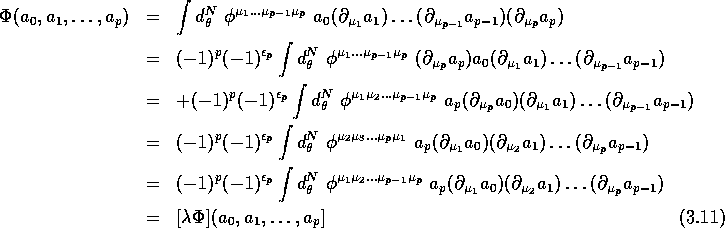
Where the symbol has the same meaning as before. In the above calculation, we use, in turn the following properties
1. The fact that a current defines a Hochschild cocycle
2. (Graded) Commutation of the element with the other elements.
3. Integration by part (with a `` + '' sign) and the fact that is closed, i.e.
4. Relabeling of indices.
5. The fact that is symmetric.
6. Definition of the cyclicity operator
Notice that the Hochschild property is translated in the fact that can be written as a current , whereas the cyclicity property imposes that this current is closed . Actually, it is exactly the same thing in the classical case of commutative calculus.
Notice also that we did not prove that all cyclic cocycles (or cyclic cohomology classes) can be expressed in terms of non-zero closed currents; indeed it is possible to exhibit a non-trivial cyclic cocycle which is trivial as a Hochschild cocycle (i.e. is a Hochschild coboundary). In such a case the corresponding current is zero. This case actually happens only when p is even and the situation is easy to control since there is only one such cyclic cohomology class that we shall call