A cyclic p-linear form is a multilinear form that is invariant (up to sign) by cyclic permutations. More precisely, the cyclicity operator , in the -graded case, is defined by
![]()
where
![]()
and is a cyclic cochain iff The cyclic complex [1] is a subcomplex of Hochschild complex. In other words, cyclic cochains of degree p on the Grassmann algebra are represented by (p+1)-linear forms on Gr(N) -i.e. Hochschild cochains - which are cyclic; their space will be denoted A cyclic cochain is therefore characterized by the value that it takes on (p+1) basis elements chosen among the that span Gr(N). Cyclic invariance shows therefore that Again this vector space is graded and The space of cyclic cocycles and coboundaries will be denoted by and with cohomology In the case of manifolds, it can be shown [1] that where denotes the homology of De Rham currents (or of differential forms, at the dual level). When De Rham (co)homology is trivial one just gets where is the boundary operator acting on currents. This result suggests, by analogy with the classical case, that one should find something similar in the Grassmannian case, i.e. we expect to be essentially given by , where is the boundary operator acting on Grassmannian currents, as defined in section 3. By ``essentially'', we mean precisely the following:
![]()
where is equal to if p is even and 0 if p is odd. This is what we show in the following. More precisely, we obtain the following results:
Closed currents can be expressed as symmetric multilinear forms on Gr(N) which are of vanishing graded divergence (i.e. ).
By direct counting, the space of such currents of degree p is a graded vector space
![]()
of dimensions and with
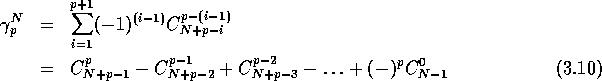
To any closed current, one can associate a cyclic cocycle.
When p is even, there will be a (unique, up to scalar multiple) canonical cyclic cocycle of degree p that we shall call . This cocycle cannot be expressed in terms of closed currents.
To any cyclic cocycle which has no component along one can associate a closed current.
An explicit basis of can therefore be found by using the previous results along with Berezin integration.
The cyclic cohomology groups are therefore where denotes the cyclic cohomology of complex numbers (it is known that and ) and where is the graded vector space introduced previously. The dimension of has been calculated in the literature by using Künneth-like formulae [5]. The novel feature here is the relation of cyclic cocycles to Grassmannian currents and their explicit expression in terms of Gr(N)-valued symmetric multilinear forms with vanishing graded divergence; as a by-product, we recover the known result concerning the dimension of .
Notice that the dimensional of the space of non-trivial cyclic cocycles is given (up to a global factor and up to 1 when p is even) by the alternated partial sums along NW-SE diagonals of the Pascal triangle.