Journée de Dynamique Non Linéaire
10h30 Luminita Danaila (CORIA, Rouen)
Caractérisation expérimentale d'un réacteur non parfaitement mélangé
Solidification d'un mélange binaire: approche en "domaine unique".
Interactions à retard et attracteurs (quasi-)périodiques dans les circuits de régulation positifs et négatifs
Résumé du séminaire de Luminita Danaila:
Dans un réacteur non-parfaitement mélangé, nous étudions expérimentalement un mélange turbulent de scalaire passif, statistiquement stationnaire, homogène et isotrope. Le réacteur est une boîte cubique, dans laquelle de l'air (pur, ou mélangé avec un scalaire) est injecté continûment via 12 jets situés sur deux faces opposées du réacteur. En utilisant des mesures ADL et PLIF, les propriétés globales et locales de l'écoulement et du mélange sont étudiées, en terme de longueurs caractéristiques, temps caractéristiques, distribution spatiale et spectrale d'énergie etc. Le nombre de Reynolds basé sur la micro-échelle de Taylor a été estimé à 60.
Différentes zones du réacteur sont distinguées: une zone d'injection et une zone centrale, dans laquelle le mélange s'effectue.
Une attention particulière a été portée sur la détermination du taux moyen de dissipation des fluctuations du scalaire passif, paramètre important pour les modèles de micro-mélange. Or, les mesures souffrent de deux pathologies: le bruit présent aux petites échelles et la résolution spatiale du système d'acquisition. Différentes méthodes de détermination du taux moyen de dissipation sont discutées: méthode spectrale, des corrélations spatio-temporelles, des fonctions de structure et des grandes échelles.
La zone centrale du réacteur est caractérisée du point de vue de l'isotropie locale et de l'intermittence interne, en utilisant plusieurs outils analytiques: corrélations spatio-temporelles, Pdfs en 1 point et en 2 points etc. A notre connaissance, c'est pour la première fois que ce genre d'analyse est effectuée sur des résultats expérimentaux, obtenus dans une turbulence statistiquement stationnaire, homogène et isotrope.
| Fig1: Dispositif expérimental. | Fig2: Image instantanée du champ scalaire, obtenue par PLIF. |
 |
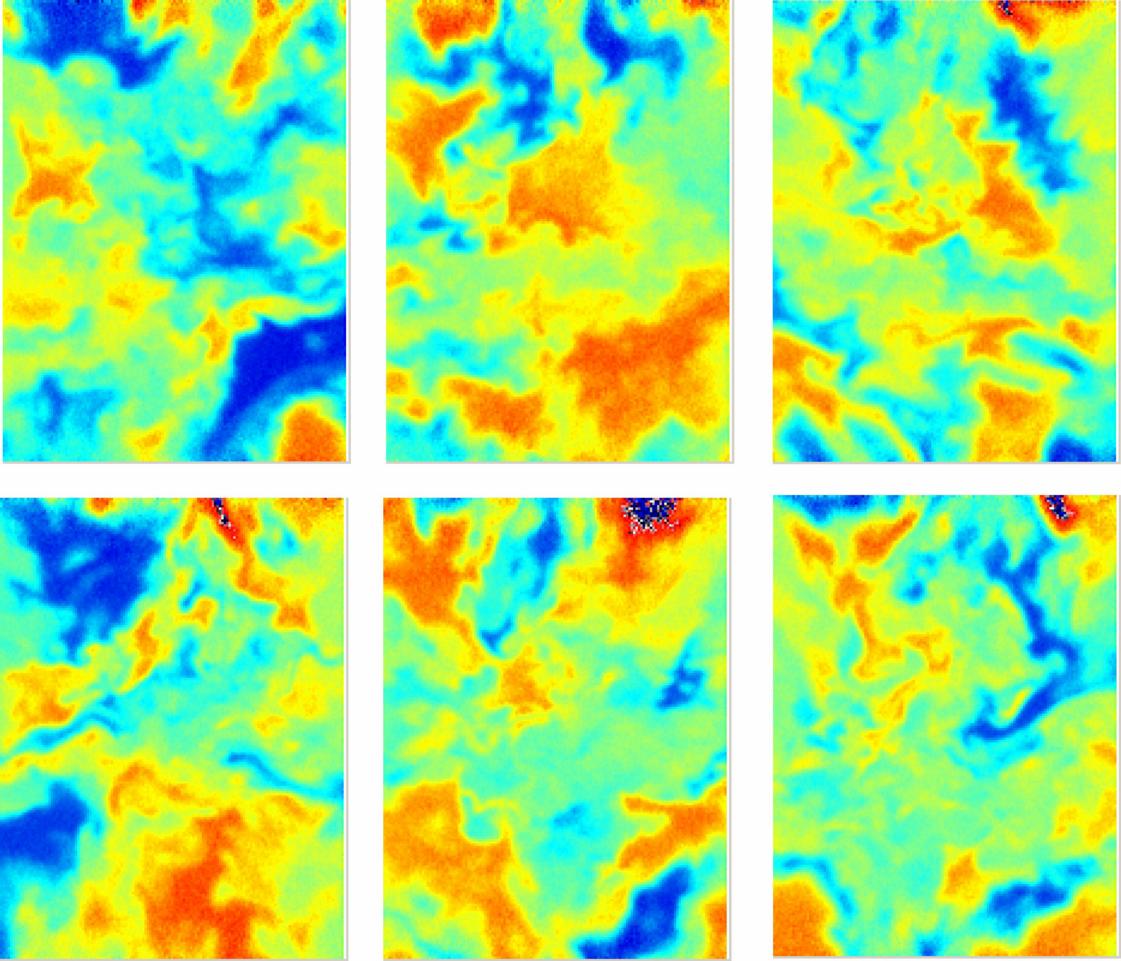 |
Résumé du séminaire de Michael Le Bars:
La solidification d'un mélange binaire engendre la formation d'un solide et le rejet d'un liquide de compositions différentes. Entre ces deux phases se développe une couche intermédiaire appelée "mush", formée d'une matrice poreuse qui évolue sans cesse, et dans laquelle des écoulements convectifs complexes prennent place. Un régime particulier se produit lorsque l'écoulement fluide se focalise dans des canaux très fins appelés "cheminées". De telles structures à petite échelle apparaissent dans divers systèmes industriels et naturels, où elles peuvent avoir des répercussions importantes à l'échelle globale (formation de fissures en sidérurgie, modification des courants océaniques au niveau des pôles, etc.).
Les processus de solidification ont fait l'objet de multiples études expérimentales, théoriques et numériques. Cependant, le fonctionnement du régime dynamique global pleinement développé n'est aujourd'hui encore que partiellement connu. Son étude exige en effet (i) le traitement simultané des trois régions (le solide, le liquide et le mush) qui interagissent activement et (ii) une résolution très fine du système afin d'observer les phénomènes à petite échelle. Jusqu'ici, les modèles proposés ont été limités à des descriptions macroscopiques ou à des configurations simplifiées, en particulier stationnaires.
En collaboration avec M.G. Worster, j'ai développé, dans une géométrie cartésienne bidimensionnelle, une simulation numérique de la solidification d'un mélange binaire, basée sur une formulation mathématique unique des équations de conservation dans les domaines solide, liquide et poreux. Contrairement à l'approche en "domaines multiples" où chaque phase est traitée séparément (i.e. Équations de Navier-Stokes dans le fluide, équation de Darcy dans le milieu poreux, etc.), cette approche en "domaine unique" ne nécessite pas d'imposer de conditions complexes et controversées aux interfaces. Le système est donc entièrement libre d'évoluer, ce qui permet d'observer entre autres la génération spontanée des cheminées. Ce modèle a été validé en comparant les résultats fournis dans quelques écoulements simples avec ceux de l'approche en "domaines multiples". Il nous a par la suite permis d'étudier précisément l'épaisseur et la composition du mush, les conditions de formation de cheminées, ainsi que leurs principales caractéristiques physiques, dans diverses situations d'intérêt géophysique et industriel.
Résumé du séminaire d'Arnaud Meyroneinc:
Les réseaux d'interactions et de régulation sont de véritables paradigmes en biologie du développement. Ils permettent de formaliser, et ainsi de mieux comprendre et prédire, la régulation de l'expression génétique et du métabolisme nécessaires au développement des organismes vivants et à leur adaptation à l'environnement. En particulier, il s'avère que certains motifs dans ces réseaux sont déterminants pour la dynamique de l'expression: les circuits positifs et les circuits négatifs en font partie. On entend par circuit positif une chaîne de gènes en interactions telle que l'action d'un gène sur lui même à travers les autres gènes de la chaîne correspond à une activation. De même, le circuit est dit négatif si l'action d'un gène sur lui même à travers les autres correspond à une inhibition. Pour ce qui est de la dynamique, il y a essentiellement deux comportements reconnus d'importance pour la biologie, les états d'équilibre stables fixes (différentiation) et (quasi-)périodiques (homéostasie, rythme circadien). Un modèle à temps discret d'applications contractantes affines par morceaux couplées est proposé afin de rendre compte de la dynamique sur de tels réseaux. Dans le cas des circuits, deux faits remarquables de la dynamique sont: la possibilité d'un attracteur (quasi-)périodique dans un circuit positif, en plus de deux points fixes, et la possibilité de la coexistance d'attracteurs (quasi-)périodiques dans un circuit négatif, dans lequel des points fixes sont impossibles. Nous discutons ces régimes dynamiques en fonction des paramètres du modèle et expliquons leurs causes (essentiellement dûs à la formalisation à temps discret qui peut être interprétée comme une modélisation d'un délai dans les interactions) dans deux cas simples, les circuits positif et négatif à deux gènes.