The theory of complex representations of quantum
groups at root of unity has been worked out by a number of people.
In the case of 
, see in particular the articles
by [29], [2] and [17].
The study of
representation theory of the finite dimensional algebra 
was
studied by [30]. Since our attitude, in the present paper, is
to study this Hopf algebra without making reference to the general theory
of quantum groups, we shall not use this last work but describe the representation theory of
by using the explicit definition of the algebra given in the
first section.
Since acts on itself (for instance from the left) one may want to consider the problem of
decomposition of this representation into irreducible or indecomposable
representations (modules). The problem
is solved by considering separately all the columns defining 
as a matrix algebra over a ring. We just
``read'' the following three indecomposable representations from the
explicit definition of (the
following should be read as ``column vectors''). First of all we have a three dimensional irreducible
representation 
, (where 
are complex
numbers) coming from 
. Notice
that the three
columns give equivalent representations. Next we
have two reducible indecomposable representations (also called ``PIM's''
for ``Projective Indecomposable Modules'') coming from the columns of
. Notice that the first two columns give
equivalent representations (that we call 
), and the last column gives the
representation 
.
Each of these two PIMS is of dimension 6.
and 
.
The notation 
for the three dimensional irreducible representation
comes from the fact that, in general algebra, such
modules are called ``Steinberg modules''. The PIM's are also called ``principal modules''.
Our notation and refers to the fact that, when expressed in
terms of Grassmann numbers, and are respectively odd and even.
and , although indecomposable, are not irreducible :
submodules (sub-representations) are immediately found
by requiring stability of the representation spaces under the left
multiplication by elements of .
At first sight (see our modifying comment below) one obtains immediately
the following lattice of submodules for the representations and
(arrows represent inclusions):
respectively generated by
, 
,
, 
for and by
,
,
,
for .
Notice that 
and that 
. 
(respectively 
) is called the socle of
(respectively of ). The module 
is the radical of and 
is
the radical of .
However, we have forgotten something. Indeed, take 
, set 
, define 
and consider the subspace 
of
spanned by 
where 
belong to
.
This subspace is clearly invariant under the left action of ;
moreover two representations corresponding to different values of
are inequivalent. Appearance of such inequivalent
representations (for different values of ) is related to the fact
that the group 
acts by exterior automorphisms on the algebra
, since it ``rotates'' the space spanned by 
and 
. Multiplying 
and 
by a
common scalar multiple amounts to change the coefficient 
so that
this family of representations is indeed parameterized by . The representations 
and 
described previously
are just two particular members of this family corresponding to the choices 
and 
.
A similar phenomenon occurs for submodules of the ``odd'' module
where we define 
The lattices of submodules of and are therefore given by
figure 1
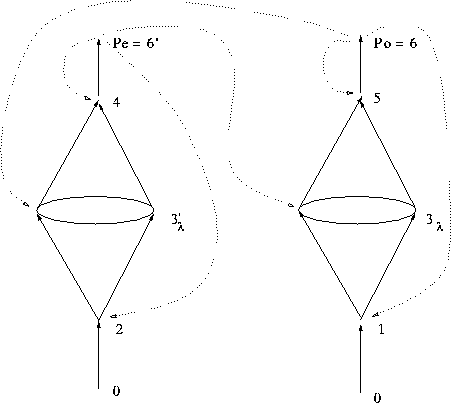
Figure 1: The lattices of submodules for the principal modules of
Since we have a totally explicit description of the algebra
and of its lattice of representations, it is easy to continue the
analysis and to investigate other properties of
illustrating many other general concepts from the study of non semi-simple associative
algebras. One can, for instance, study the projective covers of the
different representations (for completeness sake, this information is
represented by dashed lines on figure 1), the subfactor
representations, the quiver of
the algebra, its Cartan matrix etcThis, however, would be a bit
technical and more appropriate for a review paper
(see [10]).
We want only to recall that there exists a one-to-one correspondence
between irreducible representations of the algebra and
the principal modules , and . Irreducible
representations are obtained from these principal modules by factorizing
their radical, which amounts to kill the Grassmann `` 
'' variables.
From the above, we see that we obtain in this way three irreducible
representations : a representation of dimension 3, (it was already irreducible) which
is a triplet for the unitary group U(3) of the part of ,
a representation of dimension 2, 
(the quotient of by its
radical) which
is a doublet for the unitary group U(2) of the 
part of , and finally a representation of dimension 1, 
(the quotient of by its
radical), a U(1) singlet. These are the three irreducible
representations corresponding to the quotient 
of by its Jacobson radical : (namely 
).
The explicit definition given for allows one to compute any tensor
products of representations and reduce them. We have to consider the
projective
indecomposable representations ( 
,
and 
)
together with the irreducible ones ( 
, 
and ).
Here again appears a mixing between and 
via the coproduct, for instance, 
.