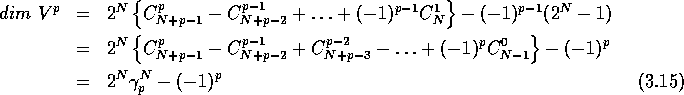
For big values of N and p, the list of algebraic constraints imposed by the equations and becomes rather large ( equations) and a direct attempt of solving these equations would become a formidable task! Fortunately, the fact that we were able to recast these constraints in terms of divergence equations for symmetric tensors will help us. We already gave the general formulae for in section 3.2 -with . We now indicate two different proofs of those results.
First method
The first method rests on an elementary induction proof and on the observation that there exists a vector space isomorphism between - that we identify here with the space of Gr(N)-valued symmetric tensors of order p - and the vector space Indeed, let a totally symmetric tensor. There are two possibilities: Either or In the first case, we have In the second case, since and Thus Therefore, we have constructed a linear map from onto with kernel . This establishes the existence of the above vector space isomorphism. Consequently The induction goes as follows: When p=0, the space is just the dual of Gr(N) - the conditions and are trivially satisfied- (actually .) The dual is, as Gr(N) itself, of dimension , and therefore (since we single out the character ). We already know the dimension of , namely . Therefore
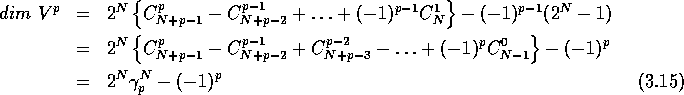
with Symmetric tensors valued in Grassmann algebras are themselves even or odd and we write, as in section 3.2, of dimensions and A simple exercise of manipulation of formal series shows that
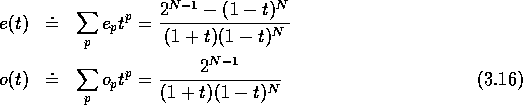
The -graded Poincaré polynomial encodes the dimension of and is defined as where is only a formal symbol. This result was already obtained in [5] using Künneth-like formulae, with no reference to currents in Grassmann algebras. Notice that the dimension of the space of cyclic cocycles itself differs from and by a trivial additive constant (the number 1) depending upon the parity of p. Indeed with in all cases but when p is odd and when p is even.
Second method
The other method amounts to compute directly the dimension of the space of those symmetric tensors that satisfy the constraint This is a rather tedious work but it is interesting because it is quite explicit and can be used to exhibit a basis of cocycles. We start from such that
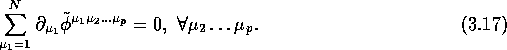
We then develop as follows
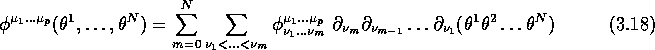
where is now real (or complex) but totally symmetric in 's and totally antisymmetric in 's. The equations to be solved read ,
![]()
Notice that for a fix m there are equations but they are not independent. A rather laborious analysis shows that, for each value of there are independent equations. This number is equal (cf appendix B) to
The dimension of the space of symmetric tensors is already known to be equal to . The dimension of is therefore equal to
![]()
The sum appearing on the right hand side can be written also as (cf appendix B)
![]()
The fact that the quantity is equal to the value given previously (first method) relies on a curious identity (proved in appendix B) between binomial coefficients, namely
![]()