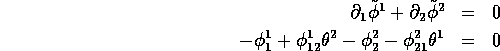
The case p=1 is of particular interest. Indeed, those cocycles can be used to construct several inequivalent cyclic cocycles on the super-circle and this, in turns, allows one to construct many inequivalent central extensions of graded loop algebras (i.e. super Kac-Moody algebras)[3]. Even, in this simple case p=1, the total number of independent cyclic one-cocycles grows rapidly with N. Previous formulae give and . Altogether In the cases N=1,2,3, for instance, one gets d =1, and . For example, in the case N=2, p=1, the most general current of degree 1 reads . Taking into account cyclic symmetry does not bring anything new in this simple case. Let us write . Then . The condition reads
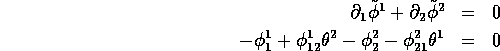
Therefore closed currents are such that , and . These three algebraic relations are independent, so we have 8-3=5 independent cocycles (closed currents). The most general one reads
![]()
Let us take, for instance, . Let , with (and a similar notation for b). The bilinear form on Gr(2) corresponding to is but so that Considering cyclic cocycles as bilinear forms on Gr(2) and using the notation introduced in eq. (3.12), one can write a basis of this space as follows.
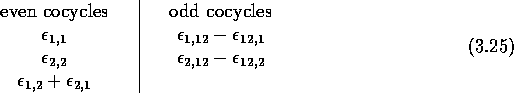
For instance, evaluated on , gives as we already know. We refer to the article [3] for more details concerning the case p=1. Since the main subject of the present article is the study of the case p>1, we wish now to illustrate the previous techniques by studying an example with p=2, N=2.