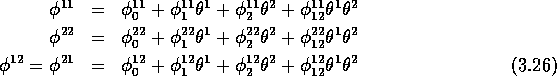
An arbitrary current of degree 2 on Gr(2) reads We recall this operator is symmetric, i.e. .
Taking into account the symmetry, we see that
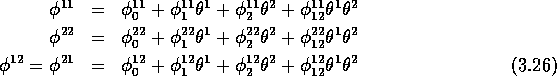
Then,
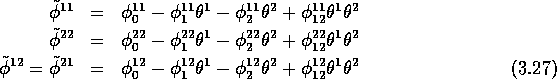
The condition read
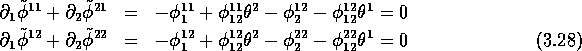
So we get the constraints
![]()
Notice that we get twice the constraint A general closed current will therefore depend on the 7 independent parameters . The most general cyclic cocycle of order 2 on Gr(2) reads therefore
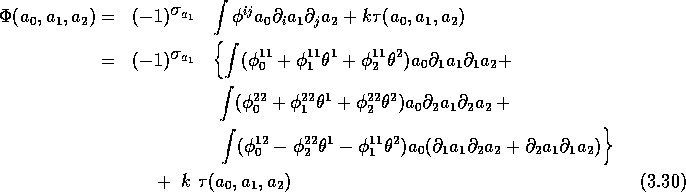
where is the canonical cocycle described in section 3.4 and k is an arbitrary constant. All these cocycles are non-trivial, (as cyclic cocycles, i.e. are not cyclic coboundaries since - with the exception of - they can be written as currents) and are inequivalent. By evaluating those Berezin integrals on the elements of a basis of Gr(2) we can rephrase the above results by saying that is generated by four even generators and four odd generators that, when expressed as (independent) multilinear forms, with a notation introduced in (3.12), read
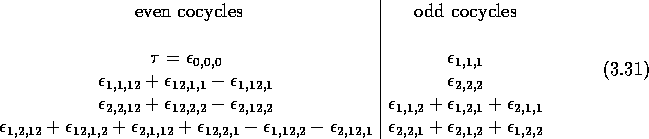
For instance, the second of the above even cocycles is a tri-linear form over Gr(2) which, when evaluated on a triple (a,b,c) gives , with , and similar decompositions for b and c.
The above construction using closed currents gives automatically non-trivial cyclic cocycles. This is an important remark. Indeed, if we had tried to solve directly ([4]) the algebraic equations and in this case, we would have found that the space of cocycles is actually and is generated therefore by three more multilinear forms that cannot be written as currents. Then, one would have had to show that these objects generate the vector space of cyclic coboundaries, so that as it should. Explicitly, one finds that coboundaries are generated by
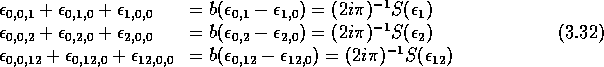
The meaning of the S operator in the above expression is explained in appendix A.
Acknowledgments
We thank the referee for a very careful reading of the manuscript and his pertinent remarks.
Appendix