Several operators called b, , A, , B, S belong to the zoo of non-commutative differential geometry. The first, the Hochschild coboundary operator b was already known before [1]. The others have been invented by [1] to replace and generalize the usual constructions of usual commutative geometry, when the algebra under study is no longer commutative. The case of Grassmann algebra is rather simple and we have been able to study its differential properties without having to introduce the operators A, , B and S. However, we feel instructive to see what is the meaning of those operators in the present context. The cyclicity operator was used in the text. is the cyclic antisymmetrizer; acting on a cyclic object -in our case a closed current on Grassmann algebra- it does essentially nothing here, besides multiplying by a trivial numerical factor. The operator is called the non-symmetrized boundary operator, it maps to and is defined by
![]()
The B operator is the symmetrized boundary operator; it also maps to and is defined by The main interest of B, in general, comes from
the fact that and Bb+Bb=0. Morally, B should be considered - up to a trivial
numerical factor- as the non-commutative generalization of the De Rham d-operator on forms, or better, since we are dealing with co-chains, as the non-commutative generalization of the
De Rham -operator acting on currents. This is known to be true in the classical case
of commutative geometry, and is clearly valid also in the Grassmannian context, since, if we
consider a closed Hochschild cochain , hence representable as a current , we see that is proportional to and is therefore associated with the current In other
words, if we had not worked out by hand the definition of the boundary operator we could have used B to define it. This explain also why we did not have to introduce B explicitly before; notice
however that action of B is defined on all Hochschild cochains (all multilinear forms on
Gr(N)) and not only on those that are representable as non-zero currents (the non-trivial
Hochschild cocycles). The operator S, in our case, brings something new. It
is called the Connes' stabilization operator, it maps ![]() to
to ![]() and is
defined as follows
and is
defined as follows
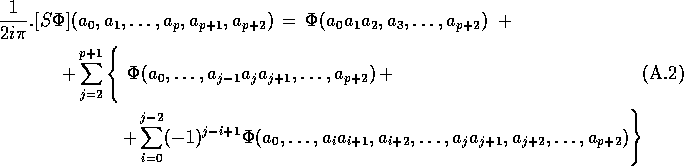
For any associative algebra, one shows [1] that S maps cyclic cochains, coboundaries and cocycles of order p to cyclic cochains, coboundaries and cocycles of order p+2 and, in particular to Also it maps cyclic cochains to Hochschild coboundaries. In particular, if , i.e. and then i.e. and but also i.e. with Notice that there is no contradiction because is not cyclic in general; in other words, if is a cyclic cocycle is always a cyclic cocycle, it may be trivial or not as a cyclic cocycle (as the b of something cyclic) but it is always trivial as a Hochschild cocycle (it is always the b of something). When translated in the particular case of Grassmann algebras, these notions read as follows.
The first observation is that the hierarchy of operators can be obtained from the first by applying powers of S:

Then, if is a non trivial cyclic cocycle of order p on Gr(N), and if we assume that it has no component along , it can be considered as a closed current. is a priori a cyclic cocycle of order p+2 but is is also a Hochschild coboundary and the associated current is zero. However, since has no component along and since we have already obtained all the cyclic cocycles of order p+2, this implies that , is not only a Hochschild coboundary but also a cyclic coboundary. In other words, as far as cyclic cohomology is concerned, and with the exception of itself, the hierarchy of cocycles is trivial: we do not get new non-trivial cocycles in this way. These remarks explain the (generic) features of the example detailed in section 3.7. To be complete we should mention that the (inductive) limit of when is called ``periodic cyclic cohomology''. The previous analysis shows that, although is, by no means, trivial, reduces to cyclic cohomology of complex numbers.