We start by proving the equality
Starting with the l.h.s. of eq. (B.1), one can rewrite it as
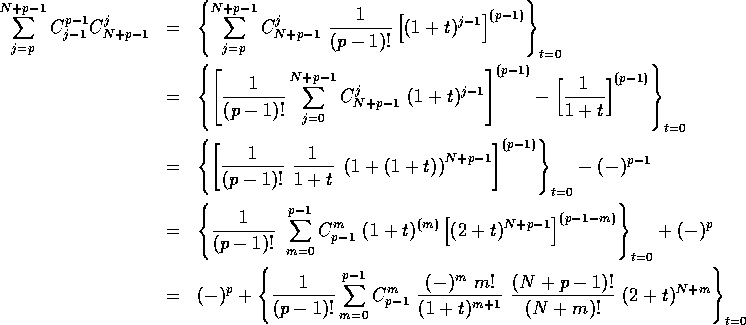
the last equality being just the r.h.s. of eq. (B.1).
Now, we prove the following identity between binomial coefficients:
![]()
We first show that
and
are equal. Indeed, they obey the same recursion relation, namely
This can be proved easily by using the addition theorem for binomial coefficients. Moreover, S(N,1)=S'(N,1) and S(N,0)=S'(N,0). Therefore
Notice that it can be useful to extend this equality for negative values of p and N by extending the Pascal's triangle upward (i.e. imposing the addition theorem for the ). By differentiating this equality enough times with respect to y, it can also be seen that the above is a remote consequence of the (Pfaff) reflection property (relating arguments z and ) of the Gauss hypergeometric function.
Setting now x=-1 and y=2 in eq. (B.3), we obtain the equality that we were looking for. It does not seem to be possible to give a simple closed form formula for the above sums, at least with the previous choice for x and y. It may be interesting to notice that a nice close formula exists when x=y=1 and this is worked out in [10].
We finish with the proof of the equality (3.20). The demonstration is quite similar to the previous one. We define
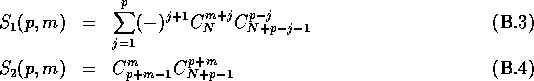
(we have drop the dependence in N because it plays no role here). These two binomial coefficient polynomials obey to the same recursion relation, namely
![]()
Moreover, it is easy to compute that , with k=1,2, , so that
![]()