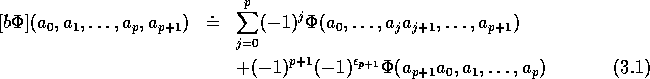
The definition of Hochschild cohomology of an arbitrary non-commutative algebra A with values in the bimodule -its dual- can be found, for instance in [1]. The Hochschild p-cochains can be taken, in the present case, as arbitrary complex-valued (p+1)-linear forms over Gr(N). Their space will be denoted by Notice that this space is naturally -graded () and that with The generalization of Hochschild cohomology to -graded algebras can be found, for instance in [9] and the corresponding coboundary operator b mapping to and satisfying is defined as follows:
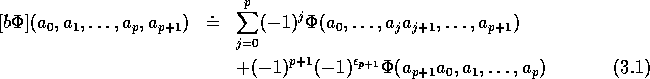
with
![]()
The space of Hochschild cocycles and coboundaries will be denoted by and with cohomology
We want to show that, in the case of Grassmann algebras, Hochschild cocycles are in one to one correspondence with p-currents. We choose therefore
![]()
where is a symmetric tensor (remember that is symmetric). The corresponding Hochschild cochain is defined by
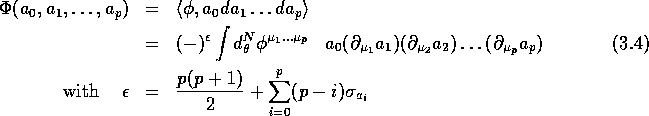
It is a simple exercise to show that , hence is a Hochschild cocycle:
Conversely, let an arbitrary p-Hochschild cocycle. It has, a priori, no reason to be symmetric. We have to symmetrize it and define a p current as:
Starting with some Hochschild cochain , one can show that if , then the current corresponding to this Hochschild coboundary is zero. Indeed, using the definition of b and, after the symmetrization process described in eq. (3.5), all the terms vanish pair-wise. This implies that we can identify the space of Grassmannian currents (elements of ) with Hochschild cohomology . As a consequence, Notice that identification of De Rham currents with Hochschild cocycles seems to be a quite general property, since it also holds in the classical case of manifolds [1] (with the difference, of course, that the dimension of grows with p in the Grassmannian case whereas it is zero as soon as p exceeds the dimension of the manifold in the classical -commutative- case). We do not study here the structure of general supermanifolds -Grassmann algebra being the simplest example- but we conjecture that, modulo an appropriate definition of currents generalizing the one given previously, the same result should hold.
Notice that a Grassmann algebra is both -graded and -graded; our previous construction of the correspondence between currents and Hochschild cocycles uses implicitly the underlying -grading. Indeed, it uses the Berezin integral, but the value of this integral will change if we make a change of chart with coefficients in rather than in C. Such a change a chart would preserve the -grading but modify the -grading.
Finally, let us remark that it may help the reader to think of Gr(N) as the fermionic Fock space built over a fermionic system with N levels (i.e. a complex vector space of dimension N) and of Hochschild p-cocycles as bosonic transitions associating a number to (p+1) elements of the fermionic Fock space (transitions are of bosonic type because of the symmetry properties of the cocycles).