Others avatars for and related algebras

In this paper, we decided to study properties of without using any a priori knowledge on quantum groups. Here are nevertheless a few (non elementary) facts, given without proof, that may interest the reader.

Consider the universal enveloping algebra of , say U. Let be the corresponding quantum algebra ( is a deformation parameter) and , K its generators (not the same as before !).

• The first way to construct the finite dimensional Hopf algebra from the infinite dimensional Hopf algebra is to divide it by an ideal (the ideal I defined by the relations given in section 3) and check that it is also a Hopf ideal (which means that , and ).

  In the usual --more precisely in the so called adjoint rational form-- and when q is a cubic root of unity, the center is generated not only by the Casimir operator but also by the elements and . It is therefore natural to define new algebras by dividing the `big' object by an ideal generated by relations of the kind we just considered (remember that in ). Actually, one could as well define new algebras by imposing relations of the kind and for integers and that are divisible by 3 (the value of the right hand side, namely 0 or 1 is fixed by the existence of a co-unit). The finite dimensional quotient therefore appears as a ``minimal'' choice. As a matter of fact, even at the level of , defined as before, and without any reference to , it is convenient to introduce an invertible square root for K, hence . In this way, one obtains a new algebra of dimension -- just count the number of independent monomials when and (this is a PBW basis). This algebra is quite interesting because its list of representations contains not only those of but also ``charge conjugate'' representations. One can also justify, for the quantum enveloping algebra itself, and whether q is a root of unity or not, the interest of adding a square root to the generator K. Introducing such a square root at the level of defines the the so-called simply-connected rational form of the quantum universal enveloping algebra. The reader should be warned that the algebra or is sometimes denoted by --with a small u-- and called the ``restricted quantum universal algebra'' (for a reason that will be explained below), but the terminology is not established yet and one should always look which of or is equal to 1; for instance, our --see above-- coincide with the K of [17].

• There exists another construction which is more tricky but maybe more profound. Let us start with the following simple observation. Consider the algebra of polynomials with one unknown x, over the rational numbers; it can be considered as an algebra generated by the (to be identified with the powers of x) with relations . One can make a change of generators, define the divided powers so that and define the very same algebra by using the new generators and the new relations. The tricky point is that, if we now decide to build an algebra over the finite field (for instance ) by taking reduction of coefficients modulo p, the two constructions, with usual powers and divided powers, will lead to two different algebras. For instance, the relation will be valid in the first algebra (the r.h.s. is non zero) whereas we obtain if we use divided powers, since 3=0 in . A similar phenomenon appears, in the case of quantum groups when q is a primitive root of unity. There are indeed two ways of specializing the q of (see for instance [3]) to a particular complex value . One can use the usual (q-deformed) generators and relations, but one can also use q-deformed divided powers and corresponding relations (these relations contain q-deformed factorials on the right hand side). For generic values of q, both definitions lead to the same algebra, but when q is a primitive root of unity, the algebras are different. More precisely, we are interested here in the ``restricted integral form'', called which is obtained as follows. We assume that , with , and start with considered as an algebra over the cyclotomic field (it is obtained by adjoining a cubic root of unity to the field Q of rational numbers). is then defined as the subalgebra of generated by the elements , where is the q factorial -- so these elements are q-deformed divided powers-- and by . Using , we see that [1]!=1, [2]!=-1 and for N>2. This, in turn, implies that, in the algebra , , is central and . contains a finite dimensional Hopf subalgebra , of dimension over , generated by and the for . Since is central, one can also construct a quotient (of dimension 27) by dividing by the relation . If we know take arbitrary complex coefficients (rather than coefficients belonging to ), we recover .
• Before ending this section, we want to comment about a rather beautiful and mysterious relation with Platonic bodies (actually with the simplest of them all, the tetrahedron). A finite Hopf algebra bearing some strong resemblance with was originally defined by [12], [13] as the restricted enveloping algebra of a simple Lie algebra over the finite field with p elements (p, a prime). The construction goes as follows :
  1. Start with an algebraic group K. In our case it will be . Note that this group, of order 24 is isomorphic with the binary tetrahedral group (the double cover of the SO(3) finite subgroup preserving a tetrahedron); the tetrahedron group itself is and is also isomorphic with the alternated group .
  2. Construct , the so-called Chevalley-Kostant -form of the universal enveloping algebra U for the corresponding Lie group G, in our case, . It is a subring (over ZZ) of U generated by the divided powers .
  3. Build the hyperalgebra of over , namely
  4. The restricted enveloping algebra is the subalgebra of the hyperalgebra spanned by the .

  The theory of restricted enveloping algebras goes back to [19] (see also his basic paper on derivations of algebras over a finite field [18]). is, in this way, defined for any Lie algebra as a subring of the corresponding enveloping algebra generated by the divided powers of the Chevalley generators. The p-powers of these generators are zero and the obtained algebra is of dimension over . For us, is Lie(SL(2,C) and so that . The purpose of defining objects like was historically to study the theory of modular representations of finite Chevalley groups. Although both , defined as a restricted enveloping algebra over a finite field, and , defined as the quotient of by the relation look like very different objects, (the first is an algebra over , the second is over or over ), it was shown by [20], [21] that there exists a natural bijection between representation theory over of the first and usual representation theory over of the second.

• Without entering this deep arithmetical discussion, we want to conclude this paragraph by a simple description of the theory of modular representations for the binary tetrahedral group . The table of usual (characteristic 0) characters of is easy to obtain, for instance from the incidence matrix of the extended Dynkin diagram of , via the McKay correspondence. The dimensions of irreducible representations are simply obtained by taking this diagram as a fusion diagram (tensorialization with the fundamental of dimension 2). One obtains in this way the seven inequivalent irreducible representations of ; see figure 2.

    
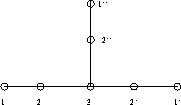
  Figure 2: Irreducible representations and fusion graph for the binary tetrahedral group
  

  Modular characters are only interesting in characteristic 2 and 3 (since primes 2 and 3 divide 24). In characteristic 3, there are only three regular conjugacy classes (namely the classes of the identity, minus the identity, and the class of the elements of period 4). Therefore, using Brauer's theory, one can check that there are also three irreducible inequivalent modular characters, of respective degrees 1, 2 and 3 (like !).