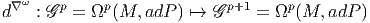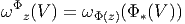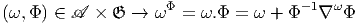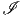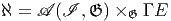Chapitre 5
Un saut dans l’infini
5.0.1 Action du groupe de jauge sur l’espace des connexions
Soit AdP = P ×AdG le fibré adjoint en groupes et adP = P ×ad𝔤 le
fibré adjoint en algèbres de Lie (voir le chapitre “Espaces fibrés”). On se
souvient que l’ensemble des sections globales de AdP n’est autre que le
groupe de jauge 𝔊 (automorphismes verticaux de P) et que l’ensemble des
sections globales de adP est l’algèbre de Lie 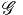 du groupe de jauge. La fibre
type de adP est une algèbre de Lie, et donc, en particulier, un espace
vectoriel. Puisque adP est un fibré vectoriel, toute connexion ω sur P
donne naissance à une différentielle covariante ∇ω agissant sur les sections
de adP (qui sont des transformations de jauge infinitésimales) et plus
généralement à une différentielle extérieure covariante d∇ω agissant sur
du groupe de jauge. La fibre
type de adP est une algèbre de Lie, et donc, en particulier, un espace
vectoriel. Puisque adP est un fibré vectoriel, toute connexion ω sur P
donne naissance à une différentielle covariante ∇ω agissant sur les sections
de adP (qui sont des transformations de jauge infinitésimales) et plus
généralement à une différentielle extérieure covariante d∇ω agissant sur
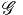 p = Ωp(M,adP).
p = Ωp(M,adP).
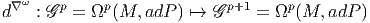 Noter que Ωp(M,adP) ≃ Ω
adp(P,Lie
Noter que Ωp(M,adP) ≃ Ω
adp(P,Lie ) (voir section 3.3.10 (2)). On supposera
aussi qu’il est possible de plonger le groupe structural G dans une algèbre de
matrices M(n, lC), pour n assez grand et donc considérer AdP comme sous-fibrés
du fibré vectoriel P ×AdM(n, lC). On peut donc également considérer la
différentielle covariante ∇ω agissant sur une transformation de jauge finie,
Φ.
) (voir section 3.3.10 (2)). On supposera
aussi qu’il est possible de plonger le groupe structural G dans une algèbre de
matrices M(n, lC), pour n assez grand et donc considérer AdP comme sous-fibrés
du fibré vectoriel P ×AdM(n, lC). On peut donc également considérer la
différentielle covariante ∇ω agissant sur une transformation de jauge finie,
Φ.
Soit  l’ensemble de toutes les connexions qu’on peut définir sur un fibré
principal donné P = P(M,G). Il est facile de voir que le groupe de jauge 𝔊 agit
sur
l’ensemble de toutes les connexions qu’on peut définir sur un fibré
principal donné P = P(M,G). Il est facile de voir que le groupe de jauge 𝔊 agit
sur  par “pull-back”. Soit Φ ∈ 𝔊, ω ∈
par “pull-back”. Soit Φ ∈ 𝔊, ω ∈  , z ∈ P et V ∈ T(P,z). On définit
ωΦ ≡ ω.Φ par
, z ∈ P et V ∈ T(P,z). On définit
ωΦ ≡ ω.Φ par
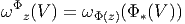
L’équivariance d’une connexion peut s’écrire, comme on le sait, en terme du
potentiel de jauge, sous la forme A → A′ = g-1Ag + g-1dg. Le second membre de
cette égalité peut encore s’écrire A + g-1(dg + [A,g]) et la quantité dg + [A,g]
apparaît comme une différentielle covariante ∇g relative à la connexion choisie.
De la même façon, l’action du groupe de jauge 𝔊 sur l’espace  des formes de
connexion s’écrit
des formes de
connexion s’écrit
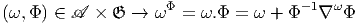
Cette loi de transformation nous montre que l’ensemble  de toutes les
connexions n’est pas un espace vectoriel mais un espace affine. En géométrie
élémentaire, la différence de deux points est un vecteur de l’espace vectoriel
sous-jacent. Il en est de même ici. L’objet Φ-1∇ωΦ est une 1-forme (équivariante)
sur P, à valeurs dans 𝔤 = Lie(G). L’espace vectoriel sous-jacent à l’espace affine
de toutes les
connexions n’est pas un espace vectoriel mais un espace affine. En géométrie
élémentaire, la différence de deux points est un vecteur de l’espace vectoriel
sous-jacent. Il en est de même ici. L’objet Φ-1∇ωΦ est une 1-forme (équivariante)
sur P, à valeurs dans 𝔤 = Lie(G). L’espace vectoriel sous-jacent à l’espace affine
 est donc
est donc 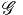 1. En particulier, notons que si ω
1 et ω2 désignent deux connexions,
alors (ω2Φ - ω
1Φ) = (ω
2 - ω1) + Φ-1(∇ω2 -∇ω1)Φ.
1. En particulier, notons que si ω
1 et ω2 désignent deux connexions,
alors (ω2Φ - ω
1Φ) = (ω
2 - ω1) + Φ-1(∇ω2 -∇ω1)Φ.
5.0.2 L’espace des orbites
Puisqu’on a une action de groupe sur un espace, on peut étudier le quotient par
cette action, c’est à dire l’espace des orbites 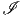 =
=  ∕𝔊. Il faut tenir compte, en
fait, de quelques subtilités car l’action de 𝔊 n’est pas libre, en général. En
d’autres termes, certaines connexions peuvent avoir des symétries : c’est le cas
lorsque le sous-groupe de 𝔊 qui stabilise une connexion donnée ne se réduit pas à
l’identité. Pour rendre cette action libre, il faut, soit considérer un espace des
connexions plus petit (c’est à dire ne considérer que les connexions “irréductibles”
pour lesquelles le stabilisateur est trivial), soit diminuer la taille du groupe de
jauge (on considère le groupe de jauge pointé 𝔊x obtenu en se fixant
arbitrairement un point x de M et en ne considérant que les transformations de
jauge Φ telles que Φ(z) = z, pour tout z appartenant à la fibre de P
au dessus de x). Moyennant ces quelques précautions, par exemple celle
qui revient à ne considérer que l’action du groupe de jauge pointé, on
montre que l’espace des connexions est lui-même un espace fibré principal,
de groupe structural 𝔊x au dessus de l’espace des orbites, qu’on note
∕𝔊. Il faut tenir compte, en
fait, de quelques subtilités car l’action de 𝔊 n’est pas libre, en général. En
d’autres termes, certaines connexions peuvent avoir des symétries : c’est le cas
lorsque le sous-groupe de 𝔊 qui stabilise une connexion donnée ne se réduit pas à
l’identité. Pour rendre cette action libre, il faut, soit considérer un espace des
connexions plus petit (c’est à dire ne considérer que les connexions “irréductibles”
pour lesquelles le stabilisateur est trivial), soit diminuer la taille du groupe de
jauge (on considère le groupe de jauge pointé 𝔊x obtenu en se fixant
arbitrairement un point x de M et en ne considérant que les transformations de
jauge Φ telles que Φ(z) = z, pour tout z appartenant à la fibre de P
au dessus de x). Moyennant ces quelques précautions, par exemple celle
qui revient à ne considérer que l’action du groupe de jauge pointé, on
montre que l’espace des connexions est lui-même un espace fibré principal,
de groupe structural 𝔊x au dessus de l’espace des orbites, qu’on note
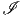 .
.
Lorsque la variété M est compacte, munie d’une métrique et qu’on a choisi
également une métrique bi-invariante sur le groupe de structure G, on peut
construire un produit scalaire global sur les espaces vectoriels 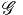 p ainsi qu’un
laplacien généralisé. Le produit scalaire sur l’espace vectoriel
p ainsi qu’un
laplacien généralisé. Le produit scalaire sur l’espace vectoriel 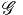 1 (identifié avec
l’espace vectoriel sous-jacent à l’espace affine
1 (identifié avec
l’espace vectoriel sous-jacent à l’espace affine  en un point quelconque ω)
fait de
en un point quelconque ω)
fait de  un espace affine euclidien (de dimension infinie, bien sûr !).
On a donc une métrique sur
un espace affine euclidien (de dimension infinie, bien sûr !).
On a donc une métrique sur  . Cette métrique permet de décomposer
l’espace tangent T(
. Cette métrique permet de décomposer
l’espace tangent T( ,ω) en un sous-espace vertical évident (celui qui
est tangent à l’action de 𝔊) et un sous-espace horizontal défini comme
étant perpendiculaire au sous-espace vertical pour cette métrique. On
obtient ainsi une connexion sur le fibré
,ω) en un sous-espace vertical évident (celui qui
est tangent à l’action de 𝔊) et un sous-espace horizontal défini comme
étant perpendiculaire au sous-espace vertical pour cette métrique. On
obtient ainsi une connexion sur le fibré  =
=  (
(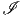 ,𝔊). La métrique sur
,𝔊). La métrique sur  ,
étant 𝔊-invariante, permet également de définir une nouvelle métrique
sur la base du fibré
,
étant 𝔊-invariante, permet également de définir une nouvelle métrique
sur la base du fibré  =
=  (
(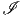 ,
, 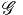 ), c’est à dire sur l’espace des orbites
), c’est à dire sur l’espace des orbites
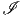 .
.
5.0.3 Conclusion
La géométrie riemannienne de l’espace des orbites des connexions, modulo
l’action du groupe de jauge, est un sujet à la fois complexe et fascinant. Notre
but, dans ce dernier chapitre n’avait d’autre but que d’entrebailler une porte…
Nous allons arrêter là notre escapade en dimension infinie, non sans faire un clin
d’œil à la physique...bouclant ainsi la boucle. En effet, on sait que dans les
théories de jauge, deux connexions qui diffèrent par une transformation de jauge
décrivent la même situation physique. L’espace des champs de Yang-Mills
possibles, celui sur lequel on doit intégrer lorsqu’on fait de la théorie quantique
des champs “à la Feynman” est donc l’espace des orbites 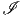 . Par ailleurs, les
champs de matière sont, comme on le sait, décrits par des sections de fibrés E
associés à un fibré principal P = P(M,G), mais le groupe de jauge 𝔊 agit sur
l’espace ΓE de ces sections et deux sections qui diffèrent par l’action du
groupe de jauge sont également physiquement équivalentes. On en déduit
que la physique des champs de Yang-Mills et des champs de matière qui
leur sont couplés est en définitive décrite par la géométrie de l’espace
fibré
. Par ailleurs, les
champs de matière sont, comme on le sait, décrits par des sections de fibrés E
associés à un fibré principal P = P(M,G), mais le groupe de jauge 𝔊 agit sur
l’espace ΓE de ces sections et deux sections qui diffèrent par l’action du
groupe de jauge sont également physiquement équivalentes. On en déduit
que la physique des champs de Yang-Mills et des champs de matière qui
leur sont couplés est en définitive décrite par la géométrie de l’espace
fibré
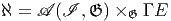 Une structure analogue existe lorsqu’on s’intéresse à la gravitation quantique et
qu’on veut étudier l’espace des métriques qu’il est possible de définir sur une
variété différentiable donnée. Le groupe de jauge 𝔊 est alors remplacé par le
groupe des difféomorphismes de M. La situation est d’ailleurs plus complexe dans
ce cas.
Une structure analogue existe lorsqu’on s’intéresse à la gravitation quantique et
qu’on veut étudier l’espace des métriques qu’il est possible de définir sur une
variété différentiable donnée. Le groupe de jauge 𝔊 est alors remplacé par le
groupe des difféomorphismes de M. La situation est d’ailleurs plus complexe dans
ce cas.
C’est donc de la géométrie différentielle en dimension infinie qu’il faut faire
pour comprendre, du point de vue quantique, la structure des théories physiques
décrivant les interactions fondamentales. Il n’est pas exclu que le traitement
mathématique le plus adapté à cette étude de la géométrie en dimension infinie
passe par une “algébraïsation” complète des techniques de la géométrie
différentielle et au remplacement de celle-ci par la géométrie non commutative
(voir chapitre suivant).
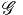 du groupe de jauge. La fibre
type de adP est une algèbre de Lie, et donc, en particulier, un espace
vectoriel. Puisque adP est un fibré vectoriel, toute connexion ω sur P
donne naissance à une différentielle covariante ∇ω agissant sur les sections
de adP (qui sont des transformations de jauge infinitésimales) et plus
généralement à une différentielle extérieure covariante d∇ω agissant sur
du groupe de jauge. La fibre
type de adP est une algèbre de Lie, et donc, en particulier, un espace
vectoriel. Puisque adP est un fibré vectoriel, toute connexion ω sur P
donne naissance à une différentielle covariante ∇ω agissant sur les sections
de adP (qui sont des transformations de jauge infinitésimales) et plus
généralement à une différentielle extérieure covariante d∇ω agissant sur
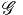 p = Ωp(M,adP).
p = Ωp(M,adP).