1.10 Orientation – Elément de volume
Déterminant – Intégration
En géométrie élémentaire, l’orientation d’un espace vectoriel réel est spécifiée par
le choix d’une base  (choix ordonné d’un système libre et générateur). Le
choix d’une autre base
(choix ordonné d’un système libre et générateur). Le
choix d’une autre base  ′ détermine un isomorphisme g qui envoie les
vecteurs de
′ détermine un isomorphisme g qui envoie les
vecteurs de  sur les vecteurs de
sur les vecteurs de  ′. On dit que g préserve l’orientation si
det g > 0 et renverse l’orientation si det g < 0. Dans le premier cas on dit
que
′. On dit que g préserve l’orientation si
det g > 0 et renverse l’orientation si det g < 0. Dans le premier cas on dit
que  et
et  ′ ont la même orientation ; dans le second cas,
′ ont la même orientation ; dans le second cas,  et
et  ′ ont
des orientations opposées. On peut alors répartir les bases de l’espace
vectoriel en question en deux classes d’équivalence correspondant aux deux
orientations possibles. Afin de généraliser cette discussion au cadre des
variétés, il est utile de reformuler ce qui précède en terme de formes
extérieures. Nous allons donc travailler avec les bases duales et poser
eμ′ = f(eμ).
′ ont
des orientations opposées. On peut alors répartir les bases de l’espace
vectoriel en question en deux classes d’équivalence correspondant aux deux
orientations possibles. Afin de généraliser cette discussion au cadre des
variétés, il est utile de reformuler ce qui précède en terme de formes
extérieures. Nous allons donc travailler avec les bases duales et poser
eμ′ = f(eμ).
Soit  * = {e1,e2,…,en} et ω = e1 ∧ e2 ∧
* = {e1,e2,…,en} et ω = e1 ∧ e2 ∧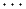 ∧ en.
∧ en.
Soit  ′* = {e1′,e2′,…,en′} avec eμ′ = f(eμ) et ω′ = f(e1) ∧ f(e2) ∧
′* = {e1′,e2′,…,en′} avec eμ′ = f(eμ) et ω′ = f(e1) ∧ f(e2) ∧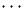 ∧ f(en).
L’espace des formes extérieures de degré n sur un espace vectoriel de dimension
n est un espace vectoriel de dimension 1. Les formes ω et ω′ sont donc
proportionnelles et le coefficient de proportionnalité n’est autre que le
déterminant de f : ω′ = (det f)ω. Nous laissons au lecteur le soin de retrouver la
définition élémentaire des déterminants en écrivant eμ′ = Λ
μμ′eμ.
∧ f(en).
L’espace des formes extérieures de degré n sur un espace vectoriel de dimension
n est un espace vectoriel de dimension 1. Les formes ω et ω′ sont donc
proportionnelles et le coefficient de proportionnalité n’est autre que le
déterminant de f : ω′ = (det f)ω. Nous laissons au lecteur le soin de retrouver la
définition élémentaire des déterminants en écrivant eμ′ = Λ
μμ′eμ.
L’orientation de l’espace vectoriel qui était définie par le choix de  peut tout
aussi bien se définir par le choix de la n-forme ω. Deux n-formes ω et ω′
(obligatoirement proportionnelles) définissent la même orientation si le coefficient
de proportionnalité est positif et deux orientations de sens contraire si le
coefficient en question est négatif. Nous pouvons maintenant passer au cas des
variétés. Nous venons de voir que l’orientation, en chaque point P de M, de
l’espace tangent TP M, est équivalente au (ou définie par le) choix d’une n-forme
extérieure en ce point. On pourrait donc naïvement penser que, pour définir une
orientation globale de la variété M, il suffit de choisir une n-forme différentiable
ω. Le problème est que, si ω s’annule en un point, l’orientation cesse d’être définie
en ce point ! Pour pouvoir parler d’orientation de façon globale, il faut
donc qu’il soit possible de choisir une n-forme différentielle sur M qui
ne s’annule nulle part. Ceci n’est pas toujours possible : on dit que la
variété est orientable ou non orientable suivant les cas. Tout le monde
connaît l’exemple fameux du ruban de Moebius ou de la bouteille de
Klein.
peut tout
aussi bien se définir par le choix de la n-forme ω. Deux n-formes ω et ω′
(obligatoirement proportionnelles) définissent la même orientation si le coefficient
de proportionnalité est positif et deux orientations de sens contraire si le
coefficient en question est négatif. Nous pouvons maintenant passer au cas des
variétés. Nous venons de voir que l’orientation, en chaque point P de M, de
l’espace tangent TP M, est équivalente au (ou définie par le) choix d’une n-forme
extérieure en ce point. On pourrait donc naïvement penser que, pour définir une
orientation globale de la variété M, il suffit de choisir une n-forme différentiable
ω. Le problème est que, si ω s’annule en un point, l’orientation cesse d’être définie
en ce point ! Pour pouvoir parler d’orientation de façon globale, il faut
donc qu’il soit possible de choisir une n-forme différentielle sur M qui
ne s’annule nulle part. Ceci n’est pas toujours possible : on dit que la
variété est orientable ou non orientable suivant les cas. Tout le monde
connaît l’exemple fameux du ruban de Moebius ou de la bouteille de
Klein.
On appelle “élément de volume” sur M le choix d’une n-forme ω sur M qui ne
s’annule nulle part (ce qui suppose, par définition, que M soit orientable). On
note [ω] l’ensemble des éléments de volume proportionnels à ω, avec un coefficient
de proportionnalité positif et [-ω] l’ensemble des éléments de volume
proportionnels à ω, avec un coefficient de proportionnalité négatif. Une variété
orientable possède donc deux orientations possibles, l’une quelconque d’entre elles
étant caractérisée par le choix d’un élément de volume appartenant à l’une des
deux classes possibles. Soient maintenant M et N deux variétés différentiables de
même dimension n et f un difféomorphisme de M dans N ; on suppose M et N
orientables et orientées par le choix des éléments de volume ωM et ωN. On dit que
f préserve l’orientation si et seulement si 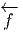 (ωN) ∈ [ωM] et renverse l’orientation
si
(ωN) ∈ [ωM] et renverse l’orientation
si 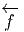 (ωN) ∈ [-ωM].
(ωN) ∈ [-ωM].
1.10.1 Orientation – Partition de l’unité
Notre but, dans ce paragraphe, est d’introduire la notion d’intégration des formes
différentielles. Comme d’habitude, on va commencer par définir cette notion
pour l’espace numérique I Rn, puis, grâce à un système de cartes, on va
pouvoir généraliser la construction au cas des variétés. On suppose le
lecteur familier avec la notion d’intégrale (de Riemann) sur I Rn. Soit f
une fonction (numérique) c’est-à-dire une fonction – que nous supposons
différentiable – de I Rn à valeurs réelles. Nous supposons, de plus, que f est à
support compact. Son intégrale est notée ∫
I Rnf ou ∫
I Rnf(x)dnx, comme
d’habitude. Choisissons maintenant une orientation sur I Rn et considérons la
n-forme
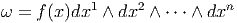 où
dx1 ∧ dx2 ∧
où
dx1 ∧ dx2 ∧ ∧ dxn est une n-forme positive pour l’orientation choisie. On pose
simplement
∧ dxn est une n-forme positive pour l’orientation choisie. On pose
simplement
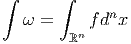 Notons que la définition du membre de gauche dépend de l’orientation choisie ;
en d’autres termes, on peut identifier les deux notations et concepts en
posant
Notons que la définition du membre de gauche dépend de l’orientation choisie ;
en d’autres termes, on peut identifier les deux notations et concepts en
posant
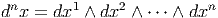 mais il faut bien noter que l’identification des notations dépend du choix d’une
orientation car l’intégrale d’une n-forme dépend de l’ordre x1,x2,…,xn
alors que l’intégrale de Riemann d’une fonction f n’en dépend pas. Soit
T un difféomorphisme de I Rn, c’est-à-dire un changement de variables
xμ
mais il faut bien noter que l’identification des notations dépend du choix d’une
orientation car l’intégrale d’une n-forme dépend de l’ordre x1,x2,…,xn
alors que l’intégrale de Riemann d’une fonction f n’en dépend pas. Soit
T un difféomorphisme de I Rn, c’est-à-dire un changement de variables
xμ yμ.
yμ.
Notre étude générale des formes différentielles implique en particulier
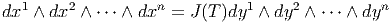 où
J(T) = det(∂xμ∕∂yν) est le jacobien (le déterminant de la matrice jacobienne) de
l’application T. On a donc
où
J(T) = det(∂xμ∕∂yν) est le jacobien (le déterminant de la matrice jacobienne) de
l’application T. On a donc
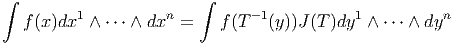 Mais on sait bien que
Mais on sait bien que
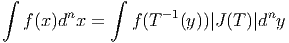 Donc si
Donc si 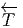 ω désigne l’image réciproque de ω, on voit que
ω désigne l’image réciproque de ω, on voit que 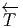 ω = ±∫
ω suivant que
T préserve ou non l’orientation : l’intégrale d’une n-forme est invariante sous le
groupe des difféomorphismes qui préservent l’orientation.
Passons maintenant au cas des variétés. Soit M une variété de dimension n et
ω une n-forme à support compact. Supposant la variété orientable, on choisit une
orientation [M] et une partition de l’unité {ρα}α∈I subordonnée à un atlas
{(Uα,φα)}α∈I, c’est-à-dire qu’on se donne une famille de fonctions différentielles
non négatives ρα telles que le support de ρα soit contenu dans Uα et
telles que ∑
ρα = 1 (chaque point de M doit posséder un voisinage dans
lequel la somme précédente est une somme finie). L’existence d’une telle
partition de l’unité, pour une variété différentiable, est un théorème
(que nous ne démontrons pas) qui permet, dans de nombreux cas, de
passer des résultats locaux (valables dans une carte) aux résultats globaux
(valables pour toute la variété M). On définit l’intégrale de ω sur [M] par
l’égalité
ω = ±∫
ω suivant que
T préserve ou non l’orientation : l’intégrale d’une n-forme est invariante sous le
groupe des difféomorphismes qui préservent l’orientation.
Passons maintenant au cas des variétés. Soit M une variété de dimension n et
ω une n-forme à support compact. Supposant la variété orientable, on choisit une
orientation [M] et une partition de l’unité {ρα}α∈I subordonnée à un atlas
{(Uα,φα)}α∈I, c’est-à-dire qu’on se donne une famille de fonctions différentielles
non négatives ρα telles que le support de ρα soit contenu dans Uα et
telles que ∑
ρα = 1 (chaque point de M doit posséder un voisinage dans
lequel la somme précédente est une somme finie). L’existence d’une telle
partition de l’unité, pour une variété différentiable, est un théorème
(que nous ne démontrons pas) qui permet, dans de nombreux cas, de
passer des résultats locaux (valables dans une carte) aux résultats globaux
(valables pour toute la variété M). On définit l’intégrale de ω sur [M] par
l’égalité
![∫ ∑ ∫
ω = ρα ω
[M] α Uα](source139x.png) où
la quantité ∫
Uαραω signifie en fait ∫
I Rn(φα-1)*(ρ
αω) pour une trivialisation
locale φα : Uα → I Rn préservant l’orientation. On se ramène ainsi au cas de
IRn.
où
la quantité ∫
Uαραω signifie en fait ∫
I Rn(φα-1)*(ρ
αω) pour une trivialisation
locale φα : Uα → I Rn préservant l’orientation. On se ramène ainsi au cas de
IRn.
L’orientation étant choisie une fois pour toutes, on note ∫
M et non plus ∫
[M]
l’intégrale correspondante. Il reste alors à démontrer que la définition adoptée ne
dépend pas des cartes choisies. . .
On appelle élément de volume sur M (de dimension n) ou forme volume un
élément quelconque ϵ de ΩnM. Le volume de M, supposée compacte, est alors
égal, par définition, à ∫
Mϵ. Il faut bien noter que sur une variété quelconque
(orientée), on intègre des n-formes, et non des fonctions, à moins, précisément,
d’avoir choisi un élément de volume ϵ une fois pour toutes, auquel cas on peut
évidemment poser ∫
Mf = ∫
Mfϵ où f ∈ C∞(M). Un cas particulièrement
important à considérer est celui où la forme volume est associée canoniquement
au choix d’une structure riemannienne (voir section 1.11) sur la variété en
question.
 (choix ordonné d’un système libre et générateur). Le
choix d’une autre base
(choix ordonné d’un système libre et générateur). Le
choix d’une autre base  ′ détermine un isomorphisme g qui envoie les
vecteurs de
′ détermine un isomorphisme g qui envoie les
vecteurs de  sur les vecteurs de
sur les vecteurs de  ′. On dit que g préserve l’orientation si
det g > 0 et renverse l’orientation si det g < 0. Dans le premier cas on dit
que
′. On dit que g préserve l’orientation si
det g > 0 et renverse l’orientation si det g < 0. Dans le premier cas on dit
que  et
et  ′ ont la même orientation ; dans le second cas,
′ ont la même orientation ; dans le second cas,  et
et  ′ ont
des orientations opposées. On peut alors répartir les bases de l’espace
vectoriel en question en deux classes d’équivalence correspondant aux deux
orientations possibles. Afin de généraliser cette discussion au cadre des
variétés, il est utile de reformuler ce qui précède en terme de formes
extérieures. Nous allons donc travailler avec les bases duales et poser
eμ′ = f(eμ).
′ ont
des orientations opposées. On peut alors répartir les bases de l’espace
vectoriel en question en deux classes d’équivalence correspondant aux deux
orientations possibles. Afin de généraliser cette discussion au cadre des
variétés, il est utile de reformuler ce qui précède en terme de formes
extérieures. Nous allons donc travailler avec les bases duales et poser
eμ′ = f(eμ).
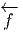 (
( (
(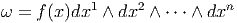

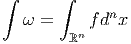
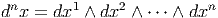
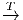
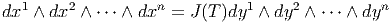
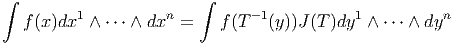
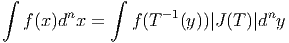
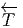
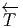
![∫ ∑ ∫
ω = ρα ω
[M] α Uα](source139x.png)