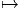ϕt ∈ Diff(M) est un homomorphisme de groupe et que l’application
(t,P) ∈ I R × M
ϕt(P) ∈ M est différentiable.
Un flot sur la variété M est un sous-groupe differentiable à un paramètre {ϕt} de
difféomorphismes de M : on suppose que pour tout t réel, l’application
t ∈ I R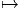ϕt ∈ Diff(M) est un homomorphisme de groupe et que l’application
(t,P) ∈ I R × Mϕt(P) ∈ M est différentiable.
La trajectoire du flot aussi appelée courbe intégrale du flot passant par le
point P ∈ M est la courbe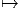 t
ϕt(P). L’application linéaire tangente à cette
courbe associe au vecteur unité 1 de R (identifié avec son espace tangent en 0) un
vecteur tangent en Q = ϕt(P) ∈ T(M,Q). Ce vecteur tangent en Q ne dépend que
du flot. En effet, les propriétés d’homomorphisme ϕt1+t2 = ϕt1 ∘ ϕt2, et de
bijectivité de ϕf , montrent que si deux trajectoires passent par le même point Q,
c’est à dire si ϕt(P1) = ϕt2(P2), avec t ≥ t2 par exemple, on peut poser t1 = t-t2
et P2 = ϕt1(P1), ce qui montre que les vecteurs tangents en Q à ces deux
trajectoires coïncident. Le vecteur tangent obtenu, notons le X(Q), définit un
champ de vecteurs X quelquefois désigné sous le nom de champ des vitesses du
flot.
Puisque le flot choisi définit un champ des vitesses, il définit également une dérivée de Lie par rapport à ce champ de vecteurs.
On peut démontrer qu’inversement, un champ de vecteurs sur une variété définit un flot local, c’est à dire qu’il ne sera en général défini que sur un ouvert strictement inclus dans I R × M ; si cette inclusion devient une égalité, le champ de vecteur est dit “complet” et il engendre un flot : les diffeomorphismes ϕt sont alors définis quel que soit t.