1.12 Divers
Nous regroupons dans ce paragraphe un certain nombre de notions et de
commentaires qui peuvent être considérés comme un peu moins élémentaires que
ce qui précède ; cela ne signifie pas qu’ils sont moins “importants” mais
simplement que nous utiliserons peu ou pas ces concepts dans la suite de
l’ouvrage. On se contente donc ici de présenter quelques définitions de façon à
suggérer au lecteur des lectures plus approfondies et à donner quelques idées
intuitives.
1.12.1 Compléments sur les dérivations d’algèbre
L’ensemble des dérivations de l’algèbre associative  se note Der
se note Der . Rappelons
qu’une dérivation est une application linéaire v de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈
. Rappelons
qu’une dérivation est une application linéaire v de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈ . Il est facile de voir que la somme
de deux dérivations est une dérivation, par contre le produit de deux
dérivations n’est pas une dérivation (dans les cas où on peut le définir,
c’est un opérateur du “second ordre” ). Il est intéressant de savoir si
l’opérateur w défini par w = hv avec h ∈
. Il est facile de voir que la somme
de deux dérivations est une dérivation, par contre le produit de deux
dérivations n’est pas une dérivation (dans les cas où on peut le définir,
c’est un opérateur du “second ordre” ). Il est intéressant de savoir si
l’opérateur w défini par w = hv avec h ∈ et v ∈ Der
et v ∈ Der est, ou non, une
dérivation. En d’autres termes, on veut savoir si l’espace Der
est, ou non, une
dérivation. En d’autres termes, on veut savoir si l’espace Der est stable
lorsqu’on multiplie (à gauche) ses éléments par des éléments de
est stable
lorsqu’on multiplie (à gauche) ses éléments par des éléments de  . Dans
l’affirmative, on dit que Der
. Dans
l’affirmative, on dit que Der est un module sur
est un module sur  . La réponse est oui, mais
seulement dans le cas où
. La réponse est oui, mais
seulement dans le cas où  est commutative. En effet, prenons f et g dans
est commutative. En effet, prenons f et g dans  .
Alors, (hv)[fg] = h(v[fg]) = h(v[f]g + fv[g]) = hv[f]g + hfv[g] mais
(hv)[f]g + f(hv)[g] = hv[f]g + fhv[g]. Ces deux expressions ne coïncident que si
hf = fh.
.
Alors, (hv)[fg] = h(v[fg]) = h(v[f]g + fv[g]) = hv[f]g + hfv[g] mais
(hv)[f]g + f(hv)[g] = hv[f]g + fhv[g]. Ces deux expressions ne coïncident que si
hf = fh.
Conclusion : L’ensemble des dérivations d’une algèbre associative n’est pas, en
général, un module sur cette algèbre, sauf si cette cette dernière est commutative.
Il est facile de voir que Der est un module sur le centre de
est un module sur le centre de  , centre qui peut
être assez petit...
, centre qui peut
être assez petit...
Par contre, l’ensemble des dérivations est toujours une algèbre de Lie : on
peut y définir une loi de composition interne (notée [, ]) non associative et
anti-commutative ([u,v] = -[v,u]), qui vérifie l’identité suivante (l’identité de
Jacobi) :
![[u,[v,w ]] + [v,[w, u]] + [w,[u,v]] = 0](source184x.png)
Rappelons que l’ensemble des champs de vecteurs sur une variété n’est autre
que l’algèbre de Lie DerC∞(M).
Le fait que l’ensemble des dérivations de  soit un module sur
soit un module sur  lorsque
lorsque  est
commutative admet une généralisation supersymétrique. Supposons que A soit
une algèbre Z Z2-graduée. Chaque élément a de
est
commutative admet une généralisation supersymétrique. Supposons que A soit
une algèbre Z Z2-graduée. Chaque élément a de  peut donc s’écrire comme
somme d’un élément pair (#a = 0) et d’un élément impair (#a = 1). On définit
les dérivations graduées (ou super-dérivations ) des algèbres Z Z2-graduées comme
les dérivations usuelles, mais en introduisant un signe. On dit qu’une
super-dérivation est paire si c’est une dérivation, au sens usuel du terme. On dit
qu’une super-dérivation est impaire si c’est une application linéaire de A dans A
telle que v[fg] = v[f]g + (-1)#ffv[g]. On introduit donc alors une Z Z
2 graduation
pour les super-dérivations et on réunit les deux types de formules de la façon
suivante :
peut donc s’écrire comme
somme d’un élément pair (#a = 0) et d’un élément impair (#a = 1). On définit
les dérivations graduées (ou super-dérivations ) des algèbres Z Z2-graduées comme
les dérivations usuelles, mais en introduisant un signe. On dit qu’une
super-dérivation est paire si c’est une dérivation, au sens usuel du terme. On dit
qu’une super-dérivation est impaire si c’est une application linéaire de A dans A
telle que v[fg] = v[f]g + (-1)#ffv[g]. On introduit donc alors une Z Z
2 graduation
pour les super-dérivations et on réunit les deux types de formules de la façon
suivante :
![|-------------------#v#f------|-
v[fg]-=-v[f]g +-(- 1-)---fv[g]--](source185x.png) avec f,g ∈
avec f,g ∈ . En pratique, il suffit d’utiliser la règle dite “Règle de Milnor”
disant qu’il faut introduire un signe “-” chaque fois qu’on doit commuter deux
éléments impairs.
. En pratique, il suffit d’utiliser la règle dite “Règle de Milnor”
disant qu’il faut introduire un signe “-” chaque fois qu’on doit commuter deux
éléments impairs.
L’ensemble des super-dérivations d’une algèbre A ne constitue pas, en général,
un module sur  , sauf lorsque
, sauf lorsque  est commutative graduée (on dit aussi
super-commutative ), c’est à dire lorsque fg = (-1)#f#ggf. Par contre l’ensemble
des dérivations graduées constitue toujours un module sur le super-centre de
est commutative graduée (on dit aussi
super-commutative ), c’est à dire lorsque fg = (-1)#f#ggf. Par contre l’ensemble
des dérivations graduées constitue toujours un module sur le super-centre de  (l’ensemble des éléments de
(l’ensemble des éléments de  qui commute – au signe près – avec
qui commute – au signe près – avec  ) et il
constitue également une super-algèbre de Lie , c’est à dire que les dérivations
graduées super-anticommutent :
) et il
constitue également une super-algèbre de Lie , c’est à dire que les dérivations
graduées super-anticommutent :
![|-----------------------|
[v,w ] = - (- )#v#w [w, v]
-------------------------](source186x.png) et
vérifient l’identité de Jacobi graduée
et
vérifient l’identité de Jacobi graduée
![|-------------------------------------------------------------|
| #u#w #w#v #v#u |
-(--)----[u,[v,w-]] +-(- )----[w,[u,v]] +-(--)---[v,[w,-u]]-=-0-](source187x.png)
1.12.2 Cohomologie de De Rham
Nous avons vu que l’opérateur d satisfait d2 = 0 et envoie ΩkM dans
Ωk+1M. Soit Zk le noyau de d, c’est-à-dire Zk = {ω ∈ ΩkM tq dω = 0}.
Les éléments de Zk sont appelés cocycles de De Rham de degré k (ou
formes fermées). Soit Bk l’image par d de Ωk-1M dans ΩkM, c’est-à-dire
Bk = {ω ∈ ΩkM tq ∃τ ∈ Ωk-1 avec ω = dτ}. Les éléments de Bk sont les
cobords de De Rham de degré k ou formes exactes . Le fait que d2 = 0 implique
l’inclusion Bk ⊂ Zk.
Il résulte de la linéarité de d que Zk et Bk sont stables par addition, ce sont
donc des groupes abéliens ; on peut alors considérer le groupe quotient
Hk = Zk∕Bk qu’on appelle groupe de cohomologie (de De Rham) de degré
k. On peut calculer, pour toute variété, les groupes H0,H1,…,Hn. Ces
groupes fournissent, en quelque sorte une “mesure” de la non-trivialité de la
topologie de la variété M. En effet, tous ces groupes sont triviaux (se
réduisent à l’élément neutre 0) dans le cas de l’espace numérique I Rn, ce que
le lecteur sait déjà puisque, dans un autre contexte, celui de la théorie
des équations différentielles sur I Rn, on montre de façon élémentaire
que, pour résoudre une équation df = 0, il faut poser f = dg (Lemme de
Poincaré).
1.12.3 Homologie de De Rham
La définition de l’homologie de De Rham est plus délicate que celle de la
cohomologie. De façon à en donner une image intuitive, disons qu’on s’intéresse à
des “morceaux” de la variété M (comptés possiblement avec multiplicité). Un tel
morceau C (techniquement une chaîne ) peut avoir un bord (le bord d’un disque
est un cercle) ou pas de bord (le bord d’un cercle est nul). On peut formellement
additionner les chaînes (avec des coefficients réels, dans le cas présent). On
définit alors un opérateur bord ∂, de carré nul lui aussi (∂2 = 0, le bord d’un
bord est nul) et on peut considérer les cycles (chaînes C dont le bord
∂C est nul) et les bords (chaînes C qui sont le bord de quelque chose
C = ∂D).
Tous les bords étant des cycles, on peut là aussi considérer les cycles Zk de
dimension k modulo les bords Bk et définir les groupes d’homologie Hk = Zk∕Bk.
De façon générale, on parle de cohomologie lorsqu’on a un opérateur de carré nul
(tel d) dont l’action sur un espace vectoriel Z Z-gradué fait croître le degré d’une
unité et d’homologie lorsqu’on a un opérateur de carré nul (tel ∂) dont l’action
fait décroître le degré.
Paradoxalement, la définition de d est plus simple que celle de ∂ (nous avons
passé cette dernière sous silence) alors que l’action de ∂ est plus intuitive, plus
“visuelle” que celle de d. Le lien entre les deux est fournit par le théorème de
Stokes : de façon générale on peut intégrer les k-formes sur les k-chaînes et on
a la propriété
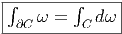 qui
généralise la relation bien connue des physiciens de première année de
nos universités ∫
Σ
qui
généralise la relation bien connue des physiciens de première année de
nos universités ∫
Σ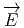 .d
.d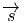 = ∫
V div
= ∫
V div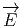 dτ où la surface Σ est le bord du
volume V et où l’intégrale représente le “flux sortant” du champ électrique
dτ où la surface Σ est le bord du
volume V et où l’intégrale représente le “flux sortant” du champ électrique
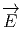 .
La dualité entre homologie et cohomologie s’écrit très simplement dans le cas
des variétés compactes ; dans ce cas, on démontre que Hk est isomorphe à
Hn-k où n est la dimension de la variété. Le support visuel intuitif suffit,
en dimension 2, pour calculer l’homologie (et donc la cohomologie) de
quelques variétés très simples. C’est ainsi que, pour la sphère S2 on a
H0(S2) = H
2(S2) = I R et H
1(S2) = 0 (tout cercle tracé sur la sphère est le bord
de quelque chose), alors que pour le tore T2, on a H
0(T2) = H
2(T2) = I R
mais H1(T2) = I R ⊕ I R : les deux générateurs de H
1(T2) correspondent
respectivement aux deux types de cercles qu’on peut tracer sur un tore et qui ne
“bordent” rien, c’est-à-dire “ceux qui font un tour”. On appelle nombres de Betti
de la variété M, la dimension bp de Hp(M) considéré comme espace
vectoriel.
.
La dualité entre homologie et cohomologie s’écrit très simplement dans le cas
des variétés compactes ; dans ce cas, on démontre que Hk est isomorphe à
Hn-k où n est la dimension de la variété. Le support visuel intuitif suffit,
en dimension 2, pour calculer l’homologie (et donc la cohomologie) de
quelques variétés très simples. C’est ainsi que, pour la sphère S2 on a
H0(S2) = H
2(S2) = I R et H
1(S2) = 0 (tout cercle tracé sur la sphère est le bord
de quelque chose), alors que pour le tore T2, on a H
0(T2) = H
2(T2) = I R
mais H1(T2) = I R ⊕ I R : les deux générateurs de H
1(T2) correspondent
respectivement aux deux types de cercles qu’on peut tracer sur un tore et qui ne
“bordent” rien, c’est-à-dire “ceux qui font un tour”. On appelle nombres de Betti
de la variété M, la dimension bp de Hp(M) considéré comme espace
vectoriel.
1.12.4 Espace des p-vecteurs
Nous avons choisi de développer la notion de produit extérieur en partant du
fibré cotangent , c’est-à-dire que nous avons considéré des produits tensoriels
complètement antisymétriques de vecteurs covariants. Ceci nous a amené
au concept de forme différentielle. Nous aurions pu faire de même en
partant des vecteurs contravariants. Le formalisme est très semblable et les
objets contravariants Ωp(M) correspondant aux formes différentielles
Ωp(M) sont simplement baptisées “p-vecteurs”. On peut alors bien entendu
évaluer une p-forme sur un p-vecteur, le résultat étant une fonction sur
M.
1.12.5 Espace des courants de De Rham
Le lecteur est sans doute déjà familier avec la notion de distribution. Pour les
fonctions numériques sur un compact de I Rn les distributions sont définies comme
dual des fonctions infiniment différentiables. Cet espace contient d’une part des
éléments “réguliers” mais aussi toutes les mesures (en particulier la mesure de
Dirac) et même des objets encore plus singuliers (les dérivées de la distribution de
Dirac par exemple). On peut généraliser la théorie des distributions aux
formes différentielles de degré quelconque sur une variété ; on définit ce
qu’on appelle l’espace des courants de De Rham comme dual (sur I R) des
formes différentielles. L’évaluation d’un courant C sur une forme ω est
donc un nombre ⟨C,ω⟩. Si la variété M est compacte et si ω est une
k-forme, un élément “régulier” peut être représenté par une n - k forme σ
puisque l’évaluation de l’intégrale ∫
Mσ ∧ ω est bien une fonctionnelle
linéaire. L’intégration d’une forme sur une chaîne (théorie de l’homologie),
l’évaluation d’un p-vecteur sur une p-forme suivie de l’intégration sur M de
la fonction obtenue, fournissent aussi des exemples de courants de De
Rham. La théorie de l’homologie de De Rham (opérateur ∂) se généralise
d’ailleurs au cadre des courants et le théorème de Stokes s’écrit dans ce cas
⟨∂C,ω⟩ = ⟨C,dω⟩.
1.12.6 Les algèbres de Frölicher – Nijenhuis et de Nijenhuis–Richardson
Nous savons que l’algèbre de De Rham Ω(M), munie du produit extérieur, est
une algèbre commutative graduée.
Nous savons aussi que l’ensemble des dérivations graduées d’une algèbre
commutative graduée constitue une super-algèbre de Lie pour laquelle le crochet
de Lie est donnée par le commutateur (gradué) que nous noterons simplement
[.,.].
En conséquence Der(Ω(M)) est une algèbre de Lie graduée. Reste à identifier
explicitement les éléments de cette algèbre.
Tout d’abord, puisque Ω(M) est Z Z-graduée, on dira qu’une dérivation est de
degré p (qui peut être positif, négatif ou nul) si elle fait passer de Ωk(M) à
Ωk+p(M). On notera Der
p(Ω(M)) l’espace des dérivations de degré p. La dérivée
extérieure est elle-même un élément de Der1(Ω(M).
Soit Ω(M,TM) l’espace des formes différentielles sur M à valeurs dans le fibré
tangent, c’est à dire Ωk(M,TM) = Γ(ΛkT*M ⊗ TM). Une k-forme K à valeurs
vectorielles s’écrira, dans un repère naturel,
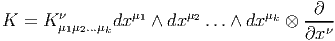
Un résultat du à Richardson et Nijenhuis montre que l’algèbre de Lie graduée
des dérivations (graduées) de l’algèbre de De Rham Ω(M) peut s’identifier à deux
copies de Ω(M,TM) munies de deux crochets différents, connus respectivement
sous le nom de crochet de Nijenhuis-Richardson et crochet de Frölicher-Nijenhuis.
Plus précisément, pour tout toute dérivation D, de degré k de l’algèbre Ω(M) on
peut trouver un unique K ∈ Ωk(M,TM) et un unique L ∈ Ωk+1(M,TM) tels
que
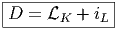 où
où
 K et iL définissent des dérivations que nous allons caractériser un peu plus loin.
Nous ne démontrerons pas le théorème de Richardson et Nijenhuis mais
définirons seulement les dérivations dont il vient d’être question (voir
[7].
K et iL définissent des dérivations que nous allons caractériser un peu plus loin.
Nous ne démontrerons pas le théorème de Richardson et Nijenhuis mais
définirons seulement les dérivations dont il vient d’être question (voir
[7].
Il se trouve que les éléments de Ω(M,TM) peuvent en effet agir par dérivation
sur Ω(M), et ce, de deux façons distinctes.
La première consiste en une généralisation du produit intérieur. Au lieu de
considérer le produit intérieur d’une forme par un vecteur, on remplace le vecteur
par une k-forme à valeurs vectorielles. En effet, soit K ∈ Ωk(M,TM),
L ∈ Ωl(M,TM) et ω une forme différentielle de degré q sur M. On va définir i
Kω,
qui sera une forme différentielle de degré k + (q - 1) (la partie “champ de
vecteurs” présente dans K fait passer de q à q - 1 mais les k indices de forme
demeurent). Soient Xi i ∈{1, 2,…,k + (q - 1) des champs de vecteurs. On
pose
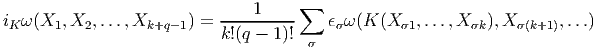 Notons que, agissant sur une fonction (un élément de Ω0(M)), i
K donne zéro. On
peut vérifier que iK défini bien une dérivation. Celle-ci est d’ailleurs de
degré k - 1 ; ainsi iK ∈ Derk-1Ω(M). On peut démontrer que toute
dérivation de l’algèbre de De Rham dont la restriction aux fonctions
est nulle est de cette forme. Le commutateur gradué (dans Der(Ω(M))
de deux dérivations de ce type est une dérivation du même type. Plus
précisément,
Notons que, agissant sur une fonction (un élément de Ω0(M)), i
K donne zéro. On
peut vérifier que iK défini bien une dérivation. Celle-ci est d’ailleurs de
degré k - 1 ; ainsi iK ∈ Derk-1Ω(M). On peut démontrer que toute
dérivation de l’algèbre de De Rham dont la restriction aux fonctions
est nulle est de cette forme. Le commutateur gradué (dans Der(Ω(M))
de deux dérivations de ce type est une dérivation du même type. Plus
précisément,
![|-----------------|
|[i ,i ] = i |
--K--L-----[K,L]NR-](source196x.png) où
la forme à valeur vectorielle [K,L]NR est égale à
où
la forme à valeur vectorielle [K,L]NR est égale à
![[K, L ]NR = iKL - (- 1)(k-1)(l-1)iLK](source197x.png) et
où on généralise l’action de iK sur Ω(M) à une action sur Ω(M,TM)
en posant iK(α ⊗ X) = iK(α) ⊗ X, avec α ∈ Ω(M) et X un champ de
vecteurs. Le crochet [,., ] porte le nom de crochet de Nijenhuis-Richardson.
et
où on généralise l’action de iK sur Ω(M) à une action sur Ω(M,TM)
en posant iK(α ⊗ X) = iK(α) ⊗ X, avec α ∈ Ω(M) et X un champ de
vecteurs. Le crochet [,., ] porte le nom de crochet de Nijenhuis-Richardson.
La deuxième façon d’agir consiste en une généralisation de la dérivée de Lie.
Soit encore K ∈ Ωk(M,TM). On définit  K par
K par
![LK = [iK ,d] = iK d - (- 1)k-1diK](source198x.png) On
peut vérifier que cet opérateur fournit bien une dérivation de l’algèbre
Ω(M). Cette dérivation est de degré k :
On
peut vérifier que cet opérateur fournit bien une dérivation de l’algèbre
Ω(M). Cette dérivation est de degré k :  K ∈ Derk(Ω(M) (dans le cas
particulier k = 0 on retrouve un résultat connu). On peut démontrer
que
K ∈ Derk(Ω(M) (dans le cas
particulier k = 0 on retrouve un résultat connu). On peut démontrer
que
![|-------------------|
[LK-,LL-] =-L[K,L]FN--](source199x.png) pour une forme à valeurs vectorielles bien déterminée notée [K,L]FN qu’on
appelle crochet de Frölicher-Nijenhuis. Pour des éléments décomposés, on a la
formule de Michor Avant de conclure ce paragraphe, il est utile de définir la notion suivante. Soit
J ∈ Ω1(M,TM), alors le carré gradué de J, pour le crochet de Frölicher-Nijenhuis,
est un élément [J,J]FN de Ω2(M,TM) appelé torsion de Nijenjuis du
vecteur-1-forme J. Pour justifier l’intérêt porté à cette notion, citons seulement le
résultat suivant (nous n’étudierons pas les variétés complexes dans cet
ouvrage) : lorsque J, qui peut s’interpréter géométriquement comme un
champ d’endomorphismes du fibré tangent, est une structure presque
complexe (J2 = -1), l’annulation de sa torsion de Nijenhuis fourni une
condition nécessaire et suffisante pour l’intégrabilité de cette structure
(c’est à dire que, dans ce cas, la structure presque-complexe est en fait,
complexe).
pour une forme à valeurs vectorielles bien déterminée notée [K,L]FN qu’on
appelle crochet de Frölicher-Nijenhuis. Pour des éléments décomposés, on a la
formule de Michor Avant de conclure ce paragraphe, il est utile de définir la notion suivante. Soit
J ∈ Ω1(M,TM), alors le carré gradué de J, pour le crochet de Frölicher-Nijenhuis,
est un élément [J,J]FN de Ω2(M,TM) appelé torsion de Nijenjuis du
vecteur-1-forme J. Pour justifier l’intérêt porté à cette notion, citons seulement le
résultat suivant (nous n’étudierons pas les variétés complexes dans cet
ouvrage) : lorsque J, qui peut s’interpréter géométriquement comme un
champ d’endomorphismes du fibré tangent, est une structure presque
complexe (J2 = -1), l’annulation de sa torsion de Nijenhuis fourni une
condition nécessaire et suffisante pour l’intégrabilité de cette structure
(c’est à dire que, dans ce cas, la structure presque-complexe est en fait,
complexe).
 se note Der
se note Der . Rappelons
qu’une dérivation est une application linéaire v de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈
. Rappelons
qu’une dérivation est une application linéaire v de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈ . Il est facile de voir que la somme
de deux dérivations est une dérivation, par contre le produit de deux
dérivations n’est pas une dérivation (dans les cas où on peut le définir,
c’est un opérateur du “second ordre” ). Il est intéressant de savoir si
l’opérateur w défini par w = hv avec h ∈
. Il est facile de voir que la somme
de deux dérivations est une dérivation, par contre le produit de deux
dérivations n’est pas une dérivation (dans les cas où on peut le définir,
c’est un opérateur du “second ordre” ). Il est intéressant de savoir si
l’opérateur w défini par w = hv avec h ∈ et v ∈ Der
et v ∈ Der est, ou non, une
dérivation. En d’autres termes, on veut savoir si l’espace Der
est, ou non, une
dérivation. En d’autres termes, on veut savoir si l’espace Der est stable
lorsqu’on multiplie (à gauche) ses éléments par des éléments de
est stable
lorsqu’on multiplie (à gauche) ses éléments par des éléments de  . Dans
l’affirmative, on dit que Der
. Dans
l’affirmative, on dit que Der est un module sur
est un module sur  . La réponse est oui, mais
seulement dans le cas où
. La réponse est oui, mais
seulement dans le cas où  est commutative. En effet, prenons f et g dans
est commutative. En effet, prenons f et g dans  .
Alors, (hv)[fg] = h(v[fg]) = h(v[f]g + fv[g]) = hv[f]g + hfv[g] mais
(hv)[f]g + f(hv)[g] = hv[f]g + fhv[g]. Ces deux expressions ne coïncident que si
hf = fh.
.
Alors, (hv)[fg] = h(v[fg]) = h(v[f]g + fv[g]) = hv[f]g + hfv[g] mais
(hv)[f]g + f(hv)[g] = hv[f]g + fhv[g]. Ces deux expressions ne coïncident que si
hf = fh.
![[u,[v,w ]] + [v,[w, u]] + [w,[u,v]] = 0](source184x.png)
![|-------------------#v#f------|-
v[fg]-=-v[f]g +-(- 1-)---fv[g]--](source185x.png)
![|-----------------------|
[v,w ] = - (- )#v#w [w, v]
-------------------------](source186x.png)
![|-------------------------------------------------------------|
| #u#w #w#v #v#u |
-(--)----[u,[v,w-]] +-(- )----[w,[u,v]] +-(--)---[v,[w,-u]]-=-0-](source187x.png)
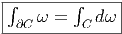
 =
= 
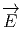 .
La dualité entre homologie et cohomologie s’écrit très simplement dans le cas
des variétés compactes
.
La dualité entre homologie et cohomologie s’écrit très simplement dans le cas
des variétés compactes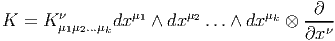
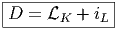

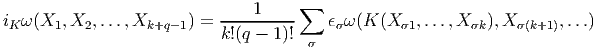
![|-----------------|
|[i ,i ] = i |
--K--L-----[K,L]NR-](source196x.png)
![[K, L ]NR = iKL - (- 1)(k-1)(l-1)iLK](source197x.png)
![LK = [iK ,d] = iK d - (- 1)k-1diK](source198x.png)
![|-------------------|
[LK-,LL-] =-L[K,L]FN--](source199x.png)
![[α ⊗ X, β ⊗ Y ]FN = α ∧ β ⊗ [X, Y ] + α ∧ LX β ⊗ Y
#α
- LY α ∧ β ⊗ X + (- 1) (dα ∧ iXβ ⊗ Y + iYα ∧ dβ ⊗ X )](source200x.png)