Les groupes de Lie et les espaces homogènes fournissent une multitude d’exemples particulièrement simples de variétés différentiables et c’est une des raisons pour lesquelles nous leur consacrons une section de cet ouvrage. Une autre raison importante est que les groupes de Lie vont être utilisés comme “outils” dans les chapitres suivants.
Chacun est censé être déjà familier avec la notion de structure de groupe. L’introduction aux groupes et leur utilisation dans toutes les branches de la physique est un thème présenté et étudié, suivant les années et les réformes de l’enseignement secondaire, entre la classe de quatrième et les années de Licence... Rappelons donc qu’un groupe est un ensemble (fini ou infini) muni d’une loi de composition interne associative, possédant un élément neutre, et tel que tout élément possède un symétrique pour la loi en question. Du point de vue du calcul, notons que, dans un groupe, il est toujours possible de résoudre une équation du premier degré (du type ax = b, la solution étant x = a-1b). Les exemples les plus simples habituellement présentés aux élèves de nos lycées sont les suivants : Le groupe (Z Z, +) des entiers relatifs, les groupes (additif et multiplicatif) de nombres rationnels (Q, +) et (Q -{0},×) ainsi que leurs généralisations réelles et complexes, les groupes de congruence Z Zp = Z Z∕pZ Z, les groupes de symétrie des solides platoniques, les groupes de transformations linéaires, affines ou projectives et les groupes de substitutions. Les groupes ne sont pas nécessairement commutatifs, comme les derniers exemples le montrent clairement. Les groupes peuvent être finis (comme Z Z∕pZ Z), infinis mais discrets (comme Z Z) ou infinis et “continus” (comme I R ou comme le groupe U(1) des rotations autour d’un axe). Regardons ce dernier exemple d’un peu plus près. Toute rotation autour d’un axe est parfaitement caractérisée par un angle θ compris entre 0 et 2π ; de surcroît, les rotations d’angle 0 et 2π sont identiques. En d’autres termes, on peut considérer les rotations en question comme les différents points d’un cercle S1 de rayon quelconque, l’élément neutre (c’est à dire la rotation d’angle nul) étant un point marqué de ce cercle S1. Ceci nous fournit un image “visuelle” de ce groupe U(1), image qui peut nous faire oublier momentanément la structure algébrique proprement dite de cet ensemble (un groupe) mais qui attire notre attention sur sa structure topologique ou même différentiable (un cercle). La notion de groupe de Lie généralise ce dernier exemple en juxtaposant de façon axiomatique la structure de groupe et celles de variété.
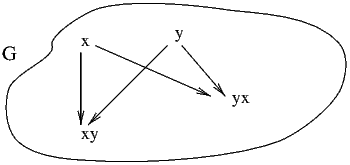
Par définition, un groupe de Lie G est donc une variété différentiable munie d’une structure de groupe, de façon à ce que les deux structures soient compatibles, c’est à dire de façon à ce que la multiplication 1 et le passage à l’inverse soient des applications différentiables. Notons que la multiplication est une application de G×G dans G alors que le passage à l’inverse est une application de G dans G. Le lecteur pourra visuellement se représenter un groupe de Lie comme un “patatoïde” avec multiplication (entre points) et origine marquée (voir 2.1).
La dimension d’un groupe de Lie est, par définition, sa dimension en tant que variété (nous verrons de nombreux exemples un peu plus loin) ; notons dès à présent que le groupe U(1) présenté plus haut est de dimension 1.
On désigne par M(n, lC) l’algèbre (de dimension complexe n2) des matrices carrées d’ordre n à coefficients complexes et par a† l’adjointe d’une matrice a de M(n, lC) (si a = (aij), alors a† = (a ji)). L’ensemble précédent n’est certes pas un groupe pour la loi de multiplication des matrices puisqu’il contient de nombreux éléments non inversibles (toutes les matrices de déterminant nul) mais il contient plusieurs sous-ensembles intéressants qui, eux, sont bien des groupes multiplicatifs, comme on pourra le vérifier aisément.
Notons que les éléments de U(n) ont automatiquement un déterminant (un nombre complexe) de module 1, puisque deta† = deta = 1∕deta, mais pas nécessairement égal à 1.
Les groupes précédents sont définis comme groupes de matrices ; les entrées de ces matrices (les “éléments de matrice”) sont des nombres qui peuvent être réels mais sont généralement complexes. Si on impose à ces éléments de matrice d’être réels, on obtient de nouveaux groupes. Soit M(n, I R) l’algèbre (de dimension réelle n2) des matrices carrées d’ordre n à coefficients réels. Cet ensemble, comme M(n, lC) est une algèbre associative mais n’est pas un groupe multiplicatif. On définit
Les éléments du groupe unitaire ayant un déterminant de module 1, ceux de O(n, I R)
auront un déterminant égal à -1 ou à 1 ; ceux pour lesquels il est précisément
égal à 1 constituent le groupe SO(n, I R). On désigne par 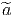 la transposée d’une
matrice a de M(n, I R).
la transposée d’une
matrice a de M(n, I R).