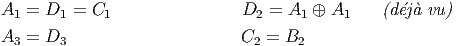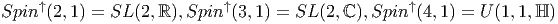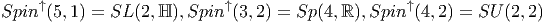2.2 Généralités sur les algèbres de Lie
2.2.1 Application exponentielle et algèbres de Lie
Définition
Une algèbre de Lie 𝔤 sur un corps commutatif I K est un ensemble qui est, d’une
part un espace vectoriel sur I K (sa loi de groupe abélien est notée + et sa loi
externe sur I K est notée multiplicativement), de dimension finie ou non, et qui,
d’autre part, est muni d’une loi de composition interne –non associative–
généralement notée [,] vérifiant les propriétés suivantes
-
Anticommutativité
- ∀X,Y ∈ 𝔤 [X,Y ] = -[Y,X]
-
Identité de Jacobi
- ∀X,Y,Z ∈ 𝔤 [X, [Y,Z]] + [Z, [X,Y ]] +
[Y, [Z,X]] = 0
On suppose également vérifiée la linéarité par rapport aux scalaires, c’est à dire
[αX,Y ] = [X,αY ] = α[X,Y ] si α ∈ I K. La loi [,] est généralement désignée sous
le nom de “crochet de Lie”. Dans toute la suite, le corps I K coïncidera avec le
corps lC des nombres complexes.
Exemple fondamental
Soit  une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
![X, Y ∈ A → [X, Y ] = XY - Y X](source203x.png) Le
crochet obtenu est généralement non nul, sauf évidemment si X et Y commutent.
Par ailleurs on vérifie aisément que les propriétés d’anticommutativité du crochet
ainsi que l’identité de Jacobi sont automatiquement satisfaites. Les ensembles de
matrices M(n, lC) et M(n, I R) sont donc automatiquement des algèbres de
Lie.
Le
crochet obtenu est généralement non nul, sauf évidemment si X et Y commutent.
Par ailleurs on vérifie aisément que les propriétés d’anticommutativité du crochet
ainsi que l’identité de Jacobi sont automatiquement satisfaites. Les ensembles de
matrices M(n, lC) et M(n, I R) sont donc automatiquement des algèbres de
Lie.
Constantes de structure d’une algèbre de Lie 𝔤
Supposons que 𝔤, en tant qu’espace vectoriel sur le corps des complexes lC soit de
dimension finie n et soit {Xα}α∈{1…n} une base de 𝔤. Le crochet de Lie [Xα,Xβ] de
deux vecteurs de base est a priori un élément de 𝔤 et peut donc se développer sur
la base choisie :
![γ
[X α,X β] = C αβX γ](source204x.png) Les
n3 nombres C
αβγ sont les constantes de structure de 𝔤 par rapport à la base
choisie.
Les
n3 nombres C
αβγ sont les constantes de structure de 𝔤 par rapport à la base
choisie.
Application exponentielle dans M(n, lC)
On désigne par exp : α →∑
p=0∞αp∕p! l’application exponentielle définie sur
M(n, lC). Posons g = eA. Il est facile de voir que
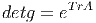 Cette relation est évidente si A est diagonalisable (puisque eλ1…eλp = eλ1+…+λp). Si
ce n’est pas le cas, on utilise pour démontrer cette propriété générale le fait que
l’ensemble des matrices diagonalisables sur lC est dense. Cette relation est à la
base d’une quantité de résultats dont voici le premier : si A ∈ M(n, lC), alors
g = eA ∈ GL(n, lC) ; en effet, detg n’est jamais nul puisque la fonction z → ez ne
s’annule pas.
Cette relation est évidente si A est diagonalisable (puisque eλ1…eλp = eλ1+…+λp). Si
ce n’est pas le cas, on utilise pour démontrer cette propriété générale le fait que
l’ensemble des matrices diagonalisables sur lC est dense. Cette relation est à la
base d’une quantité de résultats dont voici le premier : si A ∈ M(n, lC), alors
g = eA ∈ GL(n, lC) ; en effet, detg n’est jamais nul puisque la fonction z → ez ne
s’annule pas.
△ ATTENTION : On n’a pas dit que tout élément de GL(n, lC) pouvait être
atteint par la fonction exp (c’est faux !).
Cas des groupes de matrices : Correspondance entre groupes et algèbres de
Lie
Soit G un groupe de Lie défini comme sous-ensemble de M(n, lC). On définit son
algèbre de Lie notée 𝔤 ou LieG comme suit,
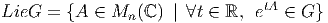 De
façon un peu imagée, on peut dire que l’algèbre de Lie d’un groupe G, c’est… son
logarithme ! De fait, l’utilisation de l’algèbre de Lie de G permet de linéariser les
propriétés des groupes, c’est à dire de transformer les multiplications en additions
etc .
De
façon un peu imagée, on peut dire que l’algèbre de Lie d’un groupe G, c’est… son
logarithme ! De fait, l’utilisation de l’algèbre de Lie de G permet de linéariser les
propriétés des groupes, c’est à dire de transformer les multiplications en additions
etc .
La définition ci-dessus de l’algèbre de Lie d’un groupe G semble un peu
restrictive en ce sens qu’elle semble ne pouvoir s’appliquer qu’aux groupes de
matrices, mais il existe une définition plus abstraite de la notion d’algèbre de Lie
d’un groupe de Lie, définition ne faisant pas l’hypothèse d’une réalisation
matricielle ; nous y reviendrons plus loin.
Soient g et h deux éléments de G et supposons qu’on puisse écrire g = etA et
h = etB avec A,B ∈ 𝔤. Tout d’abord, notons que g-1 = e-tA. On peut alors
considérer le commutateur de g et h au sens de la théorie des groupes,
c’est à dire l’élément c = ghg-1h-1 de G. Au second ordre en t, il vient
Il ne faudrait pas trop hâtivement en déduire que le commutateur dans G est égal
à l’exponentielle du commutateur dans LieG, mais c’est “presque” vrai,
comme on vient de le voir (c 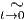 1 + t2[A,B]). De plus, on peut démontrer
que
1 + t2[A,B]). De plus, on peut démontrer
que
![t2[A,B] tA∕n tB ∕n -tA∕n -tB ∕n n2
e = nli→m∞(e e e e )](source209x.png) C’est à l’aide de ces relations qu’on peut s’assurer que l’algèbre de Lie d’un
groupe de Lie est bien… une algèbre de Lie (l’ensemble est bien stable par le
commutateur).
C’est à l’aide de ces relations qu’on peut s’assurer que l’algèbre de Lie d’un
groupe de Lie est bien… une algèbre de Lie (l’ensemble est bien stable par le
commutateur).
Soit g ∈ G et supposons qu’on puisse écrire g = eA ; alors, en utilisant la
structure d’espace vectoriel de LieG, on voit qu’on peut décomposer A sur une
base {Xα} ;ainsi, A = ∑
aαX
α. Les n nombres aα permettent donc de définir
sur G un système de coordonnées (une carte). Ceci montre également que la
dimension de G, en tant que variété, est égale à celle de LieG, considéré comme
espace vectoriel.
2.2.2 Correspondance entre groupes et algèbres de Lie
Algèbres de Lie des groupes classiques
Notons d’abord que, pour les groupes unitaires,
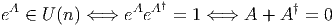 ainsi la matrice A est anti-hermitienne.
ainsi la matrice A est anti-hermitienne.
Nous avons déjà rencontré la relation deteA = eTrA ; il s’ensuit que, si le
déterminant de g = eA est égal à 1, la trace de A est nulle. Ainsi,
![A †
e ∈ SU (n) ⇐⇒ [A + A = 0 et T rA = 0]](source211x.png) Dans le cas des groupes orthogonaux, la définition implique immédiatement
Dans le cas des groupes orthogonaux, la définition implique immédiatement
![t
eA ∈ O (n) ⇐ ⇒ [eAeA = 1 et A r´eel] ⇐ ⇒ [A + At = 0 et A r´eel]](source212x.png) Les
matrices A de l’algèbre correspondante sont donc antisymétriques réelles, ce qui,
en particulier, implique la nullité des éléments de matrice diagonaux et donc de la
trace ; mais le seul fait que trA = 0 implique deteA = 1 et donc eA ∈ SO(n). Y
aurait-il une contradiction ? Comment donc obtenir une matrice orthogonale de
déterminant différent de 1 ? Il est pourtant bien évident que la définition de
O(n) est différente de celle de SO(n) ! La seule conclusion possible est la
suivante : les éléments de O(n) qui ne sont pas dans SO(n) ne sont
pas atteints par la fonction exp (voir la remarque à la fin du présent
paragraphe).
Les
matrices A de l’algèbre correspondante sont donc antisymétriques réelles, ce qui,
en particulier, implique la nullité des éléments de matrice diagonaux et donc de la
trace ; mais le seul fait que trA = 0 implique deteA = 1 et donc eA ∈ SO(n). Y
aurait-il une contradiction ? Comment donc obtenir une matrice orthogonale de
déterminant différent de 1 ? Il est pourtant bien évident que la définition de
O(n) est différente de celle de SO(n) ! La seule conclusion possible est la
suivante : les éléments de O(n) qui ne sont pas dans SO(n) ne sont
pas atteints par la fonction exp (voir la remarque à la fin du présent
paragraphe).
Pour calculer la dimension des groupes de Lie, le plus simple est en général de
calculer la dimension des algèbres de Lie correspondantes. Voici un exemple que
lecteur pourra généraliser sans peine : “Fabriquons” une matrice carrée
antihermitienne. Une matrice n × n dépend, a priori, de n2 paramètres
complexes ; nous enlevons d’abord la diagonale (donc il reste n2 - n
paramètres), puis nous fabriquons une matrice triangulaire inférieure stricte
(donc (n2 - n)∕2 paramètres) ; la partie triangulaire supérieure est
alors complètement déterminée par la condition d’anti-hermiticité ;
finalement, cette même condition implique que les éléments diagonaux
sont imaginaires purs : il nous faut donc rajouter n paramètres réels.
Au total, on a donc 2(n2 - n)∕2 + n = n2paramètres réels. Ainsi donc
dimRU(n) = dimRLieU(n) = n2.
Le lecteur pourra sans doute ainsi retrouver sans difficulté la dimension des
algèbres de Lie suivantes. Remarque : La notation Sp(n) utilisée ci-dessous
désigne le groupe unitaire-quaternionique (voir “remarques diverses” en
fin de section 2 concernant les groupes symplectiques) ; les matrices de
l’algèbre de Lie correspondante sont du type 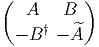 avec A† = -A et
avec A† = -A et
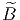 = B.
= B.
| G | LieG | dimI RG |
| | | |
|
|
|
| | | |
| GL(n, lC) | M(n, lC) | 2n2 |
| GL(n, I R) | M(n, I R) | n2 |
| U(n) | Matrices anti-hermitiennes | n2 |
| SU(n) | Matrices anti-hermitiennes de trace nulle | n2 - 1 |
| SO(n) | Matrices antisymétriques réelles | 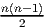 |
| Sp(n) | Voir ci-dessus | 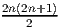 |
Remarques
- Si nous ne précisons pas davantage, c’est que les algèbres de Lie
que nous considérons sont des algèbres de Lie réelles. Il y a là une
petite subtilité que nous allons illustrer en considérant le cas de
𝔲(n) = LieU(n). Il s’agit d’ un espace vectoriel sur I R de dimension
d = n2, ce qui signifie qu’une base de cet espace vectoriel réel
possède d = n2 éléments (appelons les {X
α}α=1…d) et qu’un élément
quelconque A de 𝔲(n) peut s’écrire A = ∑
α=1daαX
α, avec des
composantes aα qui sont des nombres réels. Par contre, les éléments
{Xα} sont, dans le cas présent des matrices antihermitiennes dont
les éléments de matrice sont généralement complexes (comme ceux
de A, d’ailleurs). Pour compliquer légèrement les choses, les éléments
{Xα} qu’on appelle traditionnellement générateurs de l’algèbre de
Lie 𝔲(n) ou encore générateurs infinitésimaux, sont souvent écrits
sous la forme Xα = iY α (dans le cas de 𝔲(n) les Y α sont donc
hermitiens) et le développement de A sur la base Xα se re-écrit
A = ∑
α=1daαiY
α, de sorte que si on pose A = iB on obtient
simplement B = ∑
α=1daαY
α ; dans ce cas, il y a des facteurs i
au second membre des relations de commutation des Y α entre eux.
Pour couronner le tout les Y α sont eux-aussi quelquefois désignés sous
le nom de “générateurs infinitésimaux”, bien qu’ils n’appartiennent
même plus à l’algèbre de Lie si cette dernière est réelle !
- L’application exp est continue. L’image continue d’un espace connexe
est un espace connexe. Une algèbre de Lie est un espace vectoriel
et donc un espace connexe. L’ensemble exp 𝔤 = {eX|X ∈ 𝔤} est
donc connexe. Conclusion : si un groupe de Lie G n’est pas connexe,
les éléments qui n’appartiennent pas à la composante connexe de
l’identité ne peuvent pas être atteints par la fonction exp (ils ne
peuvent pas s’écrire sous la forme eX). Ceci montre que, dans bien
des cas, l’application exp n’est pas surjective. Le calcul effectué plus
haut et concernant le groupe orthogonal O(n) reflète le fait que ce
dernier n’est pas connexe. Par contre les groupes U(n), SU(n), SO(n)
et Sp(n) sont connexes.
Même si G est connexe, l’application exp n’est pas nécessairement
surjective. Par contre, on démontre que si G est compact et connexe,
cette application est surjective (c’est le cas de U(n), SU(n), SO(n) et
Sp(n)). Si G est connexe mais non compact, on démontre que exp est
“presque” surjective, en ce sens que
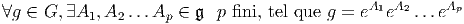
- Par définition, le rang d’un groupe de Lie compact est égal à à la
dimension d’un sous groupe abélien maximal contenu dans G (on
dit alors souvent “tore maximal” au lieu de “sous groupe abélien
maximal”).
Cette définition sera suffisante pour nous, mais voici néanmoins une
définition valable dans un contexte plus général : le rang d’un groupe
de Lie est défini comme étant celui de l’algèbre de Lie correspondante,
lui-même défini comme la dimension de l’une quelconque de ses
sous-algèbres de Cartan (si le corps de base est celui des complexes
et que l’algèbre de Lie est de dimension finie, toutes ses sous-algèbres
de Cartan sont isomorphes) ; dans ce cadre général une sous-algèbre
de Cartan est une sous-algèbre de Lie nilpotente qui coincide avec
son propre normalisateur. Dans le cas semi-simple une sous-algèbre de
Cartan est simplement une sous-algèbre de Lie abélienne maximale.
Isomorphisme local : comparaison entre SU(2) et SO(3)
Nous avons déjà vu (dans le cas du groupe orthogonal O(n)) que les éléments
d’un groupe n’appartenant pas à la composante connexe de l’identité ne
pouvaient pas être atteints par la fonction exponentielle. Pour cette raison, nous
supposerons que tous les groupes de Lie considérés dans la présente sous-section
sont connexes (cas de SO(n)). Nous nous intéressons en effet ici à des
phénomènes plus fins que la connexité.
- Soient
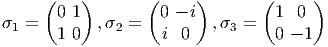 les trois matrices de Pauli. Lie(SU(2)) est l’espace vectoriel engendré
par X1,X2,X3 avec Xj = iσj∕2 puisque {X1,X2,X3} constituent
une base de l’algèbre des matrices antihermitiennes de trace nulle.
Notons que
les trois matrices de Pauli. Lie(SU(2)) est l’espace vectoriel engendré
par X1,X2,X3 avec Xj = iσj∕2 puisque {X1,X2,X3} constituent
une base de l’algèbre des matrices antihermitiennes de trace nulle.
Notons que
![[Xi, Xj] = - ϵijkXk](source219x.png) où ϵ est complètement antisymétrique et ϵ123 = 1. En développant la
fonction exponentielle en série et en utilisant les propriétés σ32 = 1,
σ2p+1 = σ
3, le lecteur montrera aisément que
où ϵ est complètement antisymétrique et ϵ123 = 1. En développant la
fonction exponentielle en série et en utilisant les propriétés σ32 = 1,
σ2p+1 = σ
3, le lecteur montrera aisément que
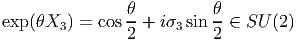 Notons que
Notons que
- Soient maintenant
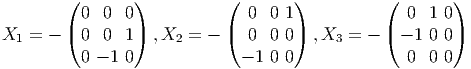 L’espace vectoriel engendré par X1,X2,X3 est constitué par l’ensemble des
matrices antisymétriques réelles 3 × 3 ; il coïncide donc avec l’algèbre de
Lie Lie(SO(3)). Comme dans le cas précèdent, on peut vérifier que
que
L’espace vectoriel engendré par X1,X2,X3 est constitué par l’ensemble des
matrices antisymétriques réelles 3 × 3 ; il coïncide donc avec l’algèbre de
Lie Lie(SO(3)). Comme dans le cas précèdent, on peut vérifier que
que
![[Xi, Xj] = - ϵijkXk](source223x.png) Les deux algèbres Lie(SO(3)) et Lie(SU(2)) sont donc isomorphes. Par
ailleurs, en développant la fonction exp en série et en utilisant les
propriétés X32p = diag((-1)p, (-1)p, 0), X
32p+1 = (-1)pX
3, il est facile de
voir que
Les deux algèbres Lie(SO(3)) et Lie(SU(2)) sont donc isomorphes. Par
ailleurs, en développant la fonction exp en série et en utilisant les
propriétés X32p = diag((-1)p, (-1)p, 0), X
32p+1 = (-1)pX
3, il est facile de
voir que
![exp [θX3 ] = diag(cosθ, cosθ,1) + X3 sin θ ∈ SO (3)](source224x.png) Notons alors que
Notons alors que
- Ainsi donc, lorsqu’“on fait un tour” dans SO(3), on revient à l’identité –
chose qu’on savait déjà ! – mais, dans SU(2), pour revenir à l’identité, il
faut faire … deux tours ! Cette différence de comportement entre les
deux groupes peut sembler assez surprenante à première vue. Il est
possible de l’illustrer de façon assez simple grâce à une expérience
élémentaire.
Expérience utilisant SO(3) : Prenez un objet quelconque, posez-le sur la
table et faites-lui subir une rotation de 360 degrés autour d’un axe
vertical ; la configuration que vous obtenez est indiscernable de la
configuration initiale.
Expérience utilisant SU(2) : Prenez un objet quelconque, suspendez-le au
milieu de la pièce en utilisant huit élastiques reliés aux huit coins (haut
et bas) de la pièce (vous pouvez utiliser un moins grand nombre
d’élastiques !) et faites subir à votre objet une rotation de 360 degrés ;
notez que les élastiques sont emmêlés ; essayez de démêler les élastiques
sans faire tourner l’objet… vous n’y parvenez pas. Faites alors subir à votre
objet une seconde rotation de 360∘ (depuis la configuration initiale vous
aurez ainsi effectué une rotation de 4π = 720∘) ; les élastiques semblent
être encore plus emmêlés ; essayez de démêler ces élastiques (retrouver la
configuration initiale) sans faire tourner l’objet… A votre grande surprise
(même si vous avez fait cette expérience plusieurs fois) vous y
parvenez !
Remarque : Si vous avez vraiment des difficultés à démêler les élastiques,
ouvrez l’ouvrage [5] où la suite des mouvements à effectuer est décrite en
détails.
Il existe une autre expérience, encore plus simple, mais un peu plus difficile
à décrire “avec des mots”, qui illustre la même différence de comportement
entre les deux groupes et qui illustre donc la façon dont SU(2) décrit les
“rotations d’objets attachés à leur environnement”. Prenez un verre
(rempli de votre vin favori) et essayez, par pivot du poignet, de lui
faire subir une rotation de 360∘… échec : à moins d’avoir des
articulations très spéciales, vous vous retrouvez tout tordu. Essayez
alors, à partir de cette position (tordue) de faire subir à votre verre
une seconde rotation, dans le même sens, de 360∘ (le coude doit
normalement s’abaisser) et ça marche : Vous vous retrouvez dans l’état
initial !
Ce phénomène amusant est d’une importance physique capitale.
C’est lui qui, en définitive, explique la différence entre fermions
et bosons (rappelons que les électrons — et plus généralement
les particules de spin demi-entier — obéissent à la statistique de
Fermi-Dirac alors que les photons (ou les noyaux d’Hélium !) — et plus
généralement les particules de spin entier — obéissent à la statistique de
Bose-Einstein.
- Revenons aux mathématiques. Nous avons un homomorphisme
de SU(2) dans SO(3) : l’image de exp(θiX
i) ∈ SU(2) est, par
définition exp(θiX
i) ∈ SO(3) où les Xi sont, bien entendu, définis de
deux façons différentes, comme précédemment. Ce morphisme
surjectif n’est pas injectif ; en effet, les deux éléments distincts
exp(2πX3) = -1 et exp(4πX3) = 1 de SU(2) se projettent tous deux sur
l’identité de SO(3). Le noyau de cet homomorphisme est donc
ZZ2 = {-1, 1} d’où il s’ensuit que SO(3) = SU(2)∕Z Z2. En effet, un
théorème très élémentaire de théorie des groupes nous apprend que si
ℓ est un homomorphisme du groupe G dans le groupe K, alors
l’image ℓ(G) est isomorphe au quotient de G par le noyau de ℓ
(dans le cadre commutatif, ce théorème généralise un résultat
bien connu et rencontré, par exemple, dans l’étude des espaces
vectoriels).
- Deux groupes possédant des algèbres de Lie isomorphes sont dits
localement isomorphes . Ainsi SU(2) et SO(3) sont localement isomorphes.
Ils ne sont cependant pas isomorphes.
On admettra le résultat suivant. Deux groupes compacts connexes non
isomorphes peuvent admettre des algèbres de Lie isomorphes (on dit qu’il s’agit
de groupes localement isomorphes). Les groupes de Lie qui admettent la même
algèbre de Lie 𝔤 sont tous de la forme Gi = G∕Di où Di est un sous-groupe
discret distingué de G. Le sous-groupe Di est isomorphe au groupe
fondamental de Gi (i.e. au premier groupe d’homotopie π1(Gi)) et le groupe
G est simplement connexe (ce qui signifie que son sous-groupe fondamental est
réduit à l’identité). G et est appelé revêtement universel de Gi. On note
quelquefois G =  i
i
- Exemples de groupes de Lie localement isomorphes.
| SU(2) et SO(3) = SU(2)∕Z Z2 | π1(SU(2)) = 1 | π1(SO(3)) = Z Z2 |
| SU(3) et SU(3)∕Z Z3 | π1(SU(3)) = 1 | π1(SU(3)∕Z Z3) = Z Z3 |
| I R et U(1) = I R∕Z Z | π1(I R) = 1 | π1(U(1)) = Z Z |
- Les groupes SO(n) ne sont jamais simplement connexes.
- Lorsque n = 2, SO(2) = U(1) = S1 et on sait que π
1(S1) = Z Z ;
le revêtement universel de U(1) est I R, l’ensemble des réels : par
définition du cercle (périodicité) on sait que U(1) = I R∕Z Z.
- Lorsque n = 3, on a vu que le revêtement universel de SO(3) est
SU(2) et que π1(SO(3)) = Z Z2.
- Lorsque n ≥ 3, on montre que π1(SO(n)) = Z Z2. Le revêtement
universel
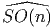 de SO(n) se note Spin(n). Le fait que Spin(3) =
SU(2) est une coïncidence de basse dimension ; on montre que
Spin(4) = SU(2)×SU(2), Spin(5) = U(2, I H) ≡ Sp(2) ≡ USp(4),
Spin(6) = SU(4).
de SO(n) se note Spin(n). Le fait que Spin(3) =
SU(2) est une coïncidence de basse dimension ; on montre que
Spin(4) = SU(2)×SU(2), Spin(5) = U(2, I H) ≡ Sp(2) ≡ USp(4),
Spin(6) = SU(4).
- Lorsque n > 6, Spin(n) n’est autre que… Spin(n) et ne coïncide
pas avec un autre groupe classique. Pour construire explicitement
Spin(n), le plus simple est d’utiliser les algèbres de Clifford (voir
la discussion en fin de chapitre).
2.2.3 Classification des groupes et algèbres de Lie. Généralités.
Un peu de terminologie
- Une algèbre de Lie est abélienne si elle est… commutative.
- Une algèbre de Lie est simple si elle n’est pas abélienne et si elle ne
possède aucun idéal bilatère non trivial.
- Une algèbre de Lie est semi-simple si elle peut s’écrire comme (si elle
est isomorphe à une) somme directe d’algèbres simples.
- Une algèbre de Lie est non semi-simple si elle n’est pas semi-simple.
On a bien entendu une terminologie analogue au niveau des groupes.
- Un groupe de Lie est abélien s’il est… commutatif.
- Un groupe de Lie est simple s’il n’est pas abélien et s’il ne possède
aucun sous groupe distingué (invariant ) non trivial.
- Un groupe de Lie est semi-simple s’il peut s’écrire comme (s’il est
isomorphe à un) produit direct de groupes simples.
- Un groupe de Lie est non semi-simple s’il n’est pas semi-simple.
Idées fondamentales de la classification
- On tente d’abord de classifier les algèbres de Lie. On en déduit la
classification des groupes de Lie. Nous supposerons toujours, dans
cette section, et sauf mention explicite du contraire, que nous sommes
en dimension finie.
- On montre qu’une algèbre de Lie quelconque peut toujours se
décomposer en une somme directe d’une algèbre de Lie semi-simple
et d’une algèbre de Lie non semi-simple particulière qu’on appelle son
radical (décomposition de Levi). Pour définir le radical d’une algèbre
de Lie 𝔤, on procède comme suit : on commence par construire la
“série dérivée” (𝔤(i)) de 𝔤 définie par 𝔤(i+1) = [𝔤(i),𝔤(i)]. Chaque terme
de cette suite est un idéal de 𝔤 contenant le terme suivant. Notons que
𝔤 est abélienne lorsque le premier terme de cette suite (c’est à dire
𝔤(1)) est nul. L’algèbre de Lie 𝔤 est dite résoluble lorsque 𝔤(k) = 0 pour
une certaine valeur de k. Etre résoluble est ainsi, pour une algèbre
de Lie, une notion un peu plus faible que celle d’être abélienne. Le
radical d’une algèbre de Lie quelconque est alors, par définition le
plus grand idéal résoluble de cette algèbre de Lie. Le radical d’une
algèbre de Lie semi-simple est, bien évidemment, nul. L’existence de
la décomposition de Levi montre qu’il faudrait classifier, pour bien
faire, d’une part les algèbres de Lie semi-simples et et d’autre part les
algèbres de Lie non semi-simples.
- La classification des algèbres de Lie non semi-simples est difficile… (et
probablement impossible).
- La classification des algèbres de Lie semi-simples (sur le corps lC) a été
effectuée par E. Cartan. Pour classer les algèbres de Lie semi-simples,
il suffit de classer les algèbres de Lie simples.
- On classifie d’abord les algèbres de Lie simples complexes (i.e. en tant
qu’espace vectoriel, le corps des complexes est lC). On démontre qu’il
existe quatre séries infinies An, Bn, Cn , Dn d’algèbres de Lie simples.
Le symbole n apparaissant en indice fournit le rang de l’algèbre
correspondante. Pour n “suffisamment petit”, il peut se faire que des
individus appartenant à des séries différentes coïncident. Il peut se
faire aussi, pour n petit, que les algèbres en question soient, non pas
simples, mais semi-simples (en fait cela n’arrive qu’une seule fois).
On y reviendra plus loin. On démontre aussi qu’il existe, en dehors
des algèbres de Lie classiques, qui sont, par définition, les membres
des quatre séries pré-citées, un nombre fini (cinq) d’algèbres de Lie
simples. On les appelle “exceptionnelles” ; ce sont : G2,F4,E6,E7 et
E8.
- Pour une algèbre de Lie complexe donnée, on classifie les différentes
algèbres de Lie réelles admettant la même extension complexe ;
techniquement, ceci se fait en classifiant les involutions. C’est ainsi
que Dn, par exemple, admet les formes réelles distinctes, notées
𝔰o(p,q),p ≥ 0,q ≥ 0,p + q = n, et 𝔰o(2n)*.
- A chaque forme réelle (c’est à dire, à chaque algèbre de Lie réelle
correspondant à une algèbre de Lie complexe donnée) on associe un
groupe de Lie connexe et simplement connexe, à l’aide de l’application
exponentielle. On démontre que, pour une algèbre de Lie complexe
donnée (exemple D3), une seule forme réelle correspond à un groupe
de Lie compact (dans notre exemple, il s’agit de
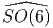 = exp(𝔰o(6)).
Les autres groupes de Lie ainsi obtenus, à savoir
= exp(𝔰o(6)).
Les autres groupes de Lie ainsi obtenus, à savoir 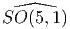 ,
, 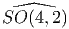 ,
,
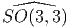 et
et 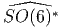 sont non compacts. L’algèbre de Lie réelle unique
dont l’exponentielle constitue un groupe de Lie compact s’appelle
forme réelle compacte de l’algèbre de Lie complexe donnée (bien que,
stricto sensu cette algèbre possède évidemment une topologie non
compacte puisqu’il s’agit d’un espace vectoriel !).
sont non compacts. L’algèbre de Lie réelle unique
dont l’exponentielle constitue un groupe de Lie compact s’appelle
forme réelle compacte de l’algèbre de Lie complexe donnée (bien que,
stricto sensu cette algèbre possède évidemment une topologie non
compacte puisqu’il s’agit d’un espace vectoriel !).
- A chaque groupe de Lie connexe et simplement connexe
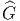 , on associe
alors une famille de groupes de Lie Gi connexes, mais non simplement
connexes en quotientant
, on associe
alors une famille de groupes de Lie Gi connexes, mais non simplement
connexes en quotientant 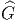 par un sous-groupe distingué discret Ki
(voir la sous-section précédente) : Gi =
par un sous-groupe distingué discret Ki
(voir la sous-section précédente) : Gi = 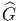 ∕Ki. On a π1(Gi) = Ki et
∕Ki. On a π1(Gi) = Ki et
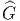 est le revêtement universel des Gi. Par exemple, on obtient ainsi
SO(6) =
est le revêtement universel des Gi. Par exemple, on obtient ainsi
SO(6) = 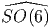 ∕Z Z2 (rappelons la notation consacrée : Spin(n) =
∕Z Z2 (rappelons la notation consacrée : Spin(n) =
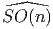 ).
).
- Les groupes de Lie compacts correspondant à la forme réelle compacte
des algèbres complexes An, Bn, Cn et Dn sont les groupes déjà
rencontrés notés SU(n + 1), Spin(2n + 1), Sp(n) et Spin(2n) dont
nous avons déjà donné les dimensions. Ceux correspondants aux
algèbres de Lie exceptionnelles se notent généralement de la même
façon que les algèbres de Lie correspondantes. Les dimensions des
cinq groupes exceptionnels G2,F4,E6,E7,E8 sont respectivement
14, 52, 78, 133, 248.
Remarques diverses
- Tout le monde, ou presque, désigne par SO(n) le groupe SO(n, I R) et
par SU(n) le groupe SU(n, lC). Les groupes de Lie correspondant à la
série Cn se notent malheureusement de façons très diverses suivant
les auteurs. Nous avons décidé de noter Sp(n) le groupe compact
correspondant et de réserver la notation Sp(2n, I R) pour désigner “le”
groupe symplectique (la forme réelle non compacte de Cn qui définit la
géométrie de l’espace des phases en mécanique). La notation U(n, I H)
se référant aux groupes unitaires quaternioniques (I H est le corps non
commutatif des quaternions) est aussi assez en vogue pour désigner le
groupe compact Sp(n). Le même groupe est désigné quelquefois par
le symbole USp(2n). La raison d’être de cette dernière notation est
que ce groupe coïncide avec l’intersection des unitaires (les U(n)) et
des symplectiques complexes (les Sp(n, lC)) Pour cette raison on les
appelle aussi “les unitaires symplectiques”. Hélas, on peut également
trouver des auteurs désignant ce même groupe USp(2n) par USp(n)…
Bref, c’est la pagaille.
- Toutes les algèbres de Lie, membres de séries An, Bn, Cn et Dn
— et tous les groupes correspondants — sont simples, à l’exception
de D2 = A1 ⊕ A1. Au niveau des groupes, on peut donc écrire
Spin(4) = SU(2)×SU(2) = Spin(3)×Spin(3) ; en d’autres termes,
SO(4) et SO(3) × SO(3) ont même algèbre de Lie.
- Comme annoncé plus haut, il existe des isomorphismes exceptionnels entre
membres de séries différentes, lorsque n est assez petit. Les voici
Au niveau des groupes compacts correspondants, on obtient donc les
isomorphismes
Citons enfin quelques isomorphismes concernant les groupes non compacts.
Spin↑(p,q) désigne ici la composante connexe de l’identité dans
Spin(p,q) :
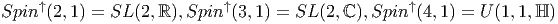
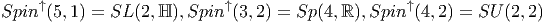
- La classification des algèbres et groupes de Lie ainsi que l’étude des
problèmes qui s’y rattachent nécessiterait de décupler la taille de
ce chapitre. Nous ne prétendons donc pas, dans ce paragraphe,
expliquer quoi que ce soit et nous nous contentons de faire un
tour rapide du zoo… Il est difficile de parler de la classification des
groupes de Lie sans mentionner les diagrammes de Dynkin (dans un
contexte différent on parle aussi de graphes de Coxeter). Mentionnons
seulement que la classification de Cartan, pour les algèbres de Lie
simples, se réduit, en fin de compte, à un problème de combinatoire
admettant une interprétation graphique. A chaque algèbre de Lie simple
complexe, on associe donc un petit diagramme (voir n’importe traité de
classification des groupes de Lie). Nous recommandons au lecteur de
compléter sa culture en allant consulter la littérature appropriée.
Notons que ces diagrammes apparaissent absolument partout, c’est à
dire non seulement dans un contexte lié à l’étude des algèbres de
Lie, mais encore dans bien d’ autres domaines : dans la théorie
des groupes engendrés par réflexions, en théorie des singularités,
dans la théorie des noeuds, dans la classification des inclusions
d’algèbres d’opérateurs (sous-facteurs), en arithmétique, dans la
géométrie des solides platoniques (en relation avec l’étude des
sous-groupes finis de SO(3)), dans la théorie des carquois, dans celle des
systèmes intégrables (en mécanique), dans les théories conformes
bi-dimensionelles, en théorie des cordes… Bref, partout. Nous espérons
donc que le lecteur, curieux, sera tenté de vouloir comprendre
pourquoi ces quelques petits dessins contiennent une telle quantité
d’information.
- Un dernier mot sur ces diagrammes : certains contiennent des
lignes doubles ou triples (exemple de G2), et d’autres non. Ceux
n’utilisant que des lignes simples (ce sont ceux des séries An, Dn et
En) sont souvent considérés, d’une certaine façon, comme plus
fondamentaux que les autres ; les algèbres de Lie correspondantes (les
algèbres “ADE”) sont également appelées algèbres simplement
lacées.
2.2.4 Message
Un tout dernier mot : passer en revue “l’essentiel” de la théorie des groupes de
Lie en une seule section – même en se limitant aux généralités et aux
problèmes de classification – est certainement une tâche impossible. Un
ouvrage entier serait d’ailleurs insuffisant. Nous n’avons fait qu’aborder
le sujet. Vouloir dresser la liste de ce qui n’a pas été effleuré serait à
la fois inutile et… incomplet ! Voici donc le message le plus important
destiné à notre lecteur néophyte : La section qui s’achève ici ne doit
pas être considérée comme un résumé, mais comme une invitation au
voyage…
 une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
 une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
une algèbre associative ; on peut lui associer canoniquement
une algèbre de Lie en définissant le crochet de Lie de la façon suivante
(auquel cas le crochet de Lie peut également être désigné sous le nom de
commutateur) :
![X, Y ∈ A → [X, Y ] = XY - Y X](source203x.png)
![γ
[X α,X β] = C αβX γ](source204x.png)
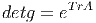
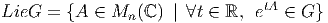
![tA tB -tA - tB
c = e e e e
= (1 + tA + t2A2∕2! + ...)(1 + tB + t2B2 ∕2! + ...)
2 2 2 2
(1 - tA + t A ∕2! + ...)(1 - tB + tB ∕2! + ...)
= 1 + 0t + t2[A, B ] + O (t3)](source207x.png)
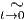 1 + t2[A,B]). De plus, on peut démontrer
que
1 + t2[A,B]). De plus, on peut démontrer
que
![t2[A,B] tA∕n tB ∕n -tA∕n -tB ∕n n2
e = nli→m∞(e e e e )](source209x.png)
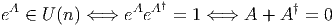
![A †
e ∈ SU (n) ⇐⇒ [A + A = 0 et T rA = 0]](source211x.png)
![t
eA ∈ O (n) ⇐ ⇒ [eAeA = 1 et A r´eel] ⇐ ⇒ [A + At = 0 et A r´eel]](source212x.png)
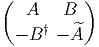 avec A† = -A et
avec A† = -A et
 = B.
= B.
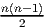
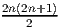
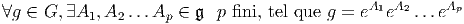
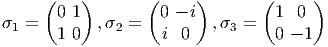
![[Xi, Xj] = - ϵijkXk](source219x.png)
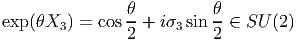
![exp[(θ + 2π)X3 ] = - exp[θX3 ]
exp[(θ + 4π)X3 ] = + exp[θX3 ]](source221x.png)
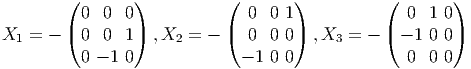
![[Xi, Xj] = - ϵijkXk](source223x.png)
![exp [θX3 ] = diag(cosθ, cosθ,1) + X3 sin θ ∈ SO (3)](source224x.png)
![exp[(θ + 2π)X3 ] = + exp[θX3 ]](source225x.png)
 i
i
 de SO(n) se note Spin(n). Le fait que Spin(3) =
SU(2) est une coïncidence de basse dimension ; on montre que
Spin(4) = SU(2)×SU(2), Spin(5) = U(2, I H) ≡ Sp(2) ≡ USp(4),
Spin(6) = SU(4).
de SO(n) se note Spin(n). Le fait que Spin(3) =
SU(2) est une coïncidence de basse dimension ; on montre que
Spin(4) = SU(2)×SU(2), Spin(5) = U(2, I H) ≡ Sp(2) ≡ USp(4),
Spin(6) = SU(4).
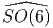 = exp(𝔰o(6)).
Les autres groupes de Lie ainsi obtenus, à savoir
= exp(𝔰o(6)).
Les autres groupes de Lie ainsi obtenus, à savoir 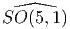 ,
, 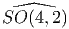 ,
,
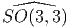 et
et 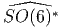 sont non compacts. L’algèbre de Lie réelle unique
dont l’exponentielle constitue un groupe de Lie compact s’appelle
forme réelle compacte de l’algèbre de Lie complexe donnée (bien que,
stricto sensu cette algèbre possède évidemment une topologie non
compacte puisqu’il s’agit d’un espace vectoriel !).
sont non compacts. L’algèbre de Lie réelle unique
dont l’exponentielle constitue un groupe de Lie compact s’appelle
forme réelle compacte de l’algèbre de Lie complexe donnée (bien que,
stricto sensu cette algèbre possède évidemment une topologie non
compacte puisqu’il s’agit d’un espace vectoriel !).
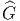 , on associe
alors une famille de groupes de Lie Gi connexes, mais non simplement
connexes en quotientant
, on associe
alors une famille de groupes de Lie Gi connexes, mais non simplement
connexes en quotientant 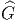 par un sous-groupe distingué discret Ki
(voir la sous-section précédente) : Gi =
par un sous-groupe distingué discret Ki
(voir la sous-section précédente) : Gi = 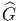 ∕Ki. On a π1(Gi) = Ki et
∕Ki. On a π1(Gi) = Ki et
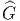 est le revêtement universel des Gi. Par exemple, on obtient ainsi
SO(6) =
est le revêtement universel des Gi. Par exemple, on obtient ainsi
SO(6) = 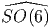 ∕Z Z2 (rappelons la notation consacrée : Spin(n) =
∕Z Z2 (rappelons la notation consacrée : Spin(n) =
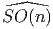 ).
).