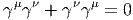
Bien connaître la structure des algèbres de Clifford est une chose essentielle, aussi bien pour les géomètres que pour les physiciens des particules, ou plus généralement pour les physiciens théoriciens. Cette section est bien trop courte pour couvrir tous leurs aspects. Nous nous contenterons de donner leur définition, de discuter leur structure générale, et de montrer comment se servir de ces algèbres pour obtenir une description explicite des groupes Spin.
L’algèbre de Clifford réelle C(p,q) est l’algèbre associative unitaire engendrée sur I R par n = p + q symboles γμ soumis aux relations (γμ)2 = 1 pour μ ∈{1, 2,…,p}, (γν)2 = -1 pour ν ∈{p + 1,p + 2,…,p + q}, et
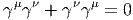
Il est utile d’introduire une matrice diagonale η = diag(1…1,-1,… - 1) et d’écrire les relations précédentes à l’aide d’un anticommutateur ({,}) sous la forme {γμ,γν,} = 2ημν
Soit E un espace vectoriel de dimension n sur I R muni d’un produit scalaire non dégénérée g (la métrique), de signature (p,q). Soit {eμ} une base orthonormée et {eμ} la base duale. On a encore une métrique de composantes gμν sur le dual. On peut associer, à tout vecteur v = vμeμ du dual, un élément Cliff(v) = vμγμ de l’algèbre de Clifford C(p,q). Abus de notations : Nous noterons v = Cliff(v). Les physiciens des particules utilisent en général la notation “slash” de Feynmann. De cette façon nous obtenons la relation uv + vu = 2g(u,v) pour tout couple de vecteurs du dual.
Une base vectorielle de C(p,q) peut être choisie comme suit :
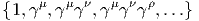
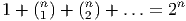
L’adjectif réel est important : Par exemple, en dimension (3, 1), l’élément γ5 = iγ0γ1γ2γ3 n’est pas un élément de C(p,q) mais un élément de l’algèbre complexifiée ClC = C(p,q) ⊗ lC.
L’algèbre C(p,q) n’est généralement pas isomorphe à C(q,p). Il faut se rappeler que (p,q) = (p+,q-).
Puisque l’algèbre de Clifford C = C(p,q) et l’algèbre extérieure Λ(E) ont même dimension, ils sont isomorphes en tant qu’espaces vectoriels. La correspondance entre les deux lois d’algèbre est la suivante : pour u,v ∈ E*, on peut directement définir le produit de Clifford uv = u ∧ v + g(u,v).
Soit C0 la partie paire de C, c’est à dire la sous-algèbre linéairement engendrée par les produits d’un nombre pair de générateurs γ.
Soit
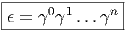
Soit Z le centre de C et Z0 le centre de C0.
Le groupe des rotations O(n) possède, comme nous l’avons vu, deux composantes connexes, mais lorsqu’on autorise une signature pseudo-euclidienne (p,q), le groupe des rotations correspondant, noté L = O(p,q) en possède en général quatre.
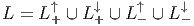
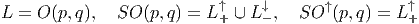
Aucune des composantes connexes de L n’est simplement connexe. Il est donc naturel de considérer, pour chacun des groupes mentionné leur groupe de recouvrement universel. On note Pin, Spin et Spin↑ les groupes simplement connexes correspondant à O, SO et SO↑.
Le groupe de Clifford Γ est défini comme l’ensemble de tous les éléments s de l’algèbre de Clifford C = C(p,q) qui sont inversibles et satisfont à la propriété :
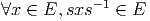
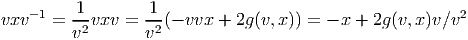
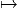 vxv-1 est donc l’opposée de la symétrie par rapport à
l’hyperplan conjugué à v. Plus généralement, pour s ∈ Γ, la transformation
vxv-1 est donc l’opposée de la symétrie par rapport à
l’hyperplan conjugué à v. Plus généralement, pour s ∈ Γ, la transformation
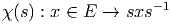
L’application χ définit manifestement une représentation du groupe de Clifford, mais cette représentation n’est pas fidèle puisque s et 3s, par exemple, déterminent la même rotation. On va obtenir le groupe Spin à partir du groupe de Clifford en introduisant une condition de normalisation. Notons tout d’abord avec une “barre”, placée au dessus d’un symbole, l’involution principale de C, définie par γμ = γμ, c’est à dire
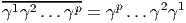
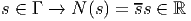
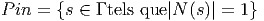
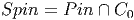
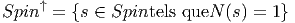
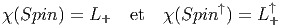
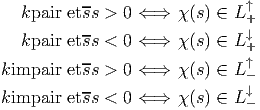
On peut non seulement décrire le groupe Spin(p,q) comme un sous ensemble de l’algèbre de Clifford C(p,q) mais aussi l’algèbre de Lie correspondante. Soient x,y,z ∈ E, alors [xy,z] ∈ E. En effet, [xy,z] = xyz -zxy = 2(xg(y,z) -g(x,z)y). En développant l’exponentielle, on obtient ainsi exp(txy)zexp(-txy) ∈ E, donc exp(txy) appartient au groupe de Clifford et xy appartient à l’algèbre de Lie du groupe de Clifford. On peut aussi, en développant l’exponentielle, montrer que exp(s) = exp(s).
Ces remarques montrent que l’algèbre de Lie du groupe de Clifford est engendrée par 1 et les produits xy lorsque x,y ∈ E. Cette algèbre de Lie est un peut trop “grosse”, celle de Spin↑ est plus intéressante. En effet, soient x et y deux (co)-vecteurs, alors
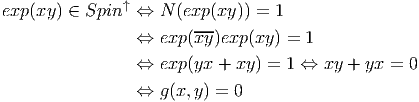
Exemple. Prenons (p = 3,q = 1). Le groupe des rotations correspondant est le groupe de Lorentz de la physique relativiste. Soit β un réel quelconque. Alors β 2 γ0γ1 ∈ Lie(Spin↑) et s = exp(β 2 γ0γ1) ∈ Spin↑. Un calcul facile (développer l’exponentielle) montre alors que
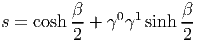
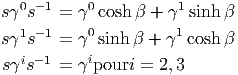
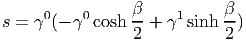
Ceci montre donc que la transformation de Lorentz χ(s) est un “boost” (rotation hyperbolique) le long de l’axe des x. Plus généralement, si
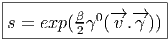
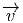 et si
et si
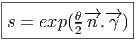
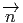 avec (|n|2 = 1).
Notons pour finir que Spin(p,q) ⊂ C0(p,q) = C0(q,p), mais que C(p,q)≠C(q,p)
en général. L’inclusion est évidente au vu de la définition du groupe Spin. Les
égalités (ou inégalités) entre ces ensembles résultent de l’étude générale qui
suit.
avec (|n|2 = 1).
Notons pour finir que Spin(p,q) ⊂ C0(p,q) = C0(q,p), mais que C(p,q)≠C(q,p)
en général. L’inclusion est évidente au vu de la définition du groupe Spin. Les
égalités (ou inégalités) entre ces ensembles résultent de l’étude générale qui
suit.
Pour voir si C ou C0 sont des algèbres simples, il faut voir si on peut, ou non, fabriquer un projecteur non trivial P (P2 = P) qui commute avec C (ou C0). Un tel projecteur peut, dans certains cas, se fabriquer à l’aide de ϵ.
La discussion est très différente suivant que la dimension n est paire ou impaire (ϵ appartiendra, suivant les cas, au centre de C, ou seulement au centre de C0).
Dans ce cas, l’opérateur d’orientation ϵ commute avec les éléments pairs de C mais anticommute avec les éléments impairs (démonstration immédiate en utilisant les relations de commutation des générateurs γμ). Le centre de C 0 est en fait engendré, dans ce cas par 1 et par ϵ.
La discussion dépend alors du carré de ϵ. Si ϵ2 = 1 on peut fabriquer deux projecteurs PR = 1+ϵ 2 et PL = 1-ϵ 2 permettant de “couper” la sous-algèbre C0 en deux composantes simples (on voit immédiatement que PL2 = P L et PR2 = P R).
La discussion peut se résumer comme suit :
C est une algèbre simple pour n pair.
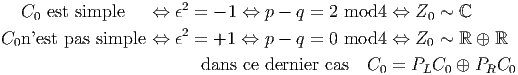
Remarque : dans le cas de l’algèbre de Dirac (nom donné à l’algèbre de Clifford dans le cas (p = 3,q = 1)), ϵ2 = -1. La sous algèbre paire C 0 est simple. Pour pouvoir la casser en deux, il faut introduire le nombre complexe i et fabriquer un projecteur (1 ± γ5)∕2 à l’aide de γ5 = iϵ, mais… cela ne peut évidemment se faire qu’en autorisant des coefficients complexes, c’est à dire en complexifiant l’algèbre C.
Dans ce cas, l’opérateur d’orientation ϵ commute avec les éléments impairs de C et commute aussi avec les éléments impairs (démonstration immédiate en utilisant les relations de commutation des générateurs γμ). Le centre de C est en fait engendré, dans ce cas par 1 et par ϵ.
La discussion dépend encore alors, comme précédemment du carré de ϵ. Si ϵ2 = 1 on peut fabriquer deux projecteurs 1+ϵ 2 et 1-ϵ 2 permettant de “couper” l’algèbre de Clifford C en deux composantes simples.
La discussion peut se résumer comme suit :
C0 est une algèbre simple.

De plus, C = C0 ⊕ C0ϵ.
La discussion qui précède pourrait laisser croire que la structure des algèbres de Clifford sur I R dépend de (p - q) modulo 4. En fait une analyse plus fine montre qu’elle dépend de (p - q) modulo 8. L’idée est la suivante : on commence par étudier explicitement la structure de quelques algèbres de Clifford de basse dimension, puis on construit les autres par produits tensoriels.
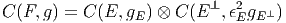
Ce théorème permet d’obtenir immédiatement les résultats suivants : Soit E un espace vectoriel de dimension 2. Soit ϵ = γ1γ2 son opérateur d’orientation.
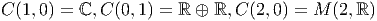
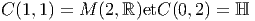
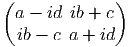
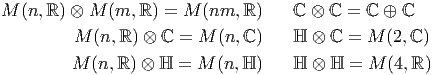
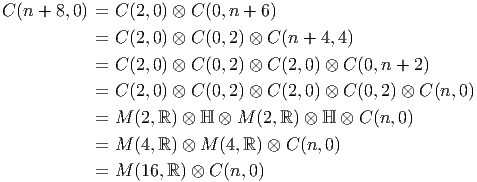
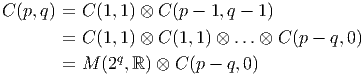
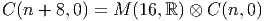
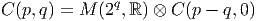
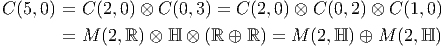
Les théorèmes de périodicité montrent alors que
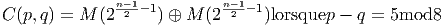
| p - qmod8 | 0 | 1 | 2 | 3 |
| C(p,q) | M(2n∕2, I R) | M(2n-1 2 , I R) ⊕ M(2n-1 2 , I R) | M(2n∕2, I R) | M(2n-1 2 , lC) |
| p - qmod8 | 4 | 5 | 6 | 7 |
| C(p,q) | M(2n 2 -1, I H) | M(2n-1 2 , I H) ⊕ M(2n-1 2 , I H) | M(2n 2 -1, I H) | M(2n-1 2 , lC) |
Le lecteur pourra faire usage des deux tables suivantes (qui se déduisent de la précédente) où on étudie explicitement le cas particulier d’une signature euclidenne (n, 0) ou (0,n) et d’une signature hyperbolique (n- 1, 1) ou (1,n- 1), pour les huit cas n = 4…11.
Cas euclidien (de n = 4 à n = 11).
Pour réduire la taille de la table, on a noté M(d,K) sous la forme (d,K).
| n | ClC | C(n, 0) | C(0,n) | C0(n, 0) | θ |
| 4 | (4, lC) | (2, I H) | (2, I H) | I H ⊕ I H | ϵ |
| 5 | (4, lC) ⊕ (4, lC) | (2, I H) ⊕ (2, I H) | (4, lC) | (2, I H) | |
| 6 | (8, lC) | (4, I H) | (8, I R) | (4, lC) | iϵ |
| 7 | (8, lC) ⊕ (8, lC) | (8, lC) | (8, I R) ⊕ (8, I R) | (8, I R) | |
| 8 | (16, lC) | (16, I R) | (16, I R) | (8, I R) ⊕ (8, I R) | ϵ |
| 9 | (16, lC) ⊕ (16, lC) | (16, I R) ⊕ (16, I R) | (16, lC) | (16, I R) | |
| 10 | (32, lC) | (32, I R) | (16, I H) | (16, lC) | iϵ |
| 11 | (32, lC) ⊕ (32, lC) | (32, lC) | (16, I H) ⊕ (16, I H) | (16, I H) | |
Cas hyperbolique (de n = 4 à n = 11).
Pour réduire la taille de la table, on a noté M(d,K) sous la forme (d,K).
| n | ClC | C(n - 1, 1) | C(1,n - 1) | C0(n - 1, 1) | θ |
| 4 | (4, lC) | (4, I R) | (2, I H) | (2, lC) | iϵ |
| 5 | (4, lC) ⊕ (4, lC) | (4, lC) | (2, I H) ⊕ (2, I H) | (2, I H) | |
| 6 | (8, lC) | (4, I H) | (4, I H) | (2, I H) ⊕ (2, I H) | ϵ |
| 7 | (8, lC) ⊕ (8, lC) | (4, I H) ⊕ (4, I H) | (8, lC) | (4, I H) | |
| 8 | (16, lC) | (8, I H) | (16, I R) | (8, lC) | iϵ |
| 9 | (16, lC) ⊕ (16, lC) | (16, lC) | (16, I R) ⊕ (16, I R) | (16, I R) | |
| 10 | (32, lC) | (32, I R) | (32, I R) | (16, I R) ⊕ (16, I R) | ϵ |
| 11 | (32, lC) ⊕ (32, lC) | (32, I R) ⊕ (32, I R) | (32, lC) | (32, I R) | |
Remarque : en observant ces tables, on voit que
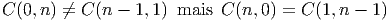
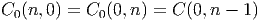
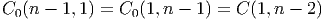
Ces dernières égalités constituent un cas particulier de la relation générale (conséquence directe des relations de périodicité) :
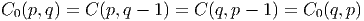
On sait que le groupe Spin(p,q) est inclus dans la sous-algèbre de Clifford paire C0(p,q). Les tables ci-dessus permettent donc aussi de trouver les inclusions de Spin(p,q) dans les groupes SL(n,K) où K = I R, lC, I H. Dans les cas de plus basse dimension, les inclusions peuvent être des égalités. Par exemple Spin(5) = SL(2, I H), Spin(10) ⊂ SL(16, lC), Spin(6, 1) ⊂ SL(4, I H) etc.
Si on complexifie l’algèbre de Clifford réelle C, c’est à dire si on autorise les scalaires de l’algèbre à appartenir au corps des nombres complexes, on peut alors toujours fabriquer, à l’aide de ϵ, un opérateur de carré un. Cet opérateur est appelé opérateur de chiralité et noté traditionnellement γ5. Si ϵ est déjà de carré égal à 1, il n’y a plus rien à faire et on pose simplement γ5 = ϵ. Sinon, on le multiplie par i et on pose γ5 = iϵ. A l’aide de cet opérateur de carré 1 on peut alors toujours fabriquer 2 projecteurs 1±γ5 2 à l’aide desquels on pourra décomposer C0lC en deux composantes simples lorsque n est pair et ClC en deux composantes simples lorsque n est impair. La discussion se résume par :
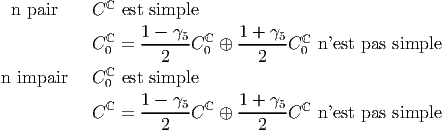
Remarque : Lorsque n est impair, on dit parfois que γ5 n’existe pas… Il faut préciser ce qu’on entend par là : l’opérateur que nous venons de définir et de noter γ5 existe dans tous les cas. Cela dit, dans le cas impair, il ne peut pas servir à décomposer C0lC en deux, précisément parce que, dans ce cas C0lC est simple ! En d’autre termes, lorsque n est impair, on ne peut pas écrire un spineur de Dirac comme somme de deux spineurs de Weyl (terminologie précisée un peu plus bas).
On dit qu’une représentation d’une K-algèbre associative A sur le K-espace vectoriel V est de type F si l’ensemble des automorphismes de V qui commutent avec l’action de A est égal à F. On démontre que F = GLA(V ) est un corps et que K est un sous-corps de F. Lorsque la représentation est irréductible et K = I R, les seules possibilités pour F sont I R, lC ou I H. Les tables qui précèdent illustrent ce phénomène. En effet, lorsqu’on écrit, par exemple C(1, 3) = M(2, I H), c’est qu’il existe, entre ces deux objets, un isomorphisme d’algèbre associative réelle. En d’autres termes, il existe une représentation fidèle ρ de la I R-algèbre C(1, 3) sur l’espace vectoriel I H2 considéré comme espace vectoriel réel de dimension 8. Les générateurs γμ sont alors représentés par des matrices 2 × 2 notées ρ(γμ) à coefficients dans I H. Il est évident que si ψ ∈ I H2 et si k ∈ I H, alors (ρ(γμ)ψ)k = ρ(γμ)(ψk), ce qui montre que le commutant de la représentation ρ est bien égal à I H : ρ est de type I H. Bien entendu, si on se donne explicitement la représentation ρ par la donnée de matrices ρ(γμ), on peut fabriquer une infinité de représentations équivalentes en changeant simplement de base. Attention, l’algèbre de Clifford C(p,q) est définie par des générateurs γμ particuliers obéissant aux relations de Clifford, alors que ce n’est pas le cas a priori pour une algèbre de matrices donnée. Il est bon de garder à l’esprit la distinction entre ces algèbres de Clifford “abstraites” et les algèbres de matrices qui les représentent fidèlement, algèbres qui sont données par les tables précédentes. On parlera cependant abusivement du type de l’algèbre C(p,q).
Dans le cas n pair, on voit, en consultant la table, que le type est toujours, soit réel, soit quaternionique.
Dans le cas n impair, les trois types peuvent exister mais on peut noter que si C(p,q) est de type complexe, alors C(q,p) est de type réel ou de type quaternionique (on n’a jamais deux types complexes en même temps pour des signatures opposées).
On peut aussi changer de point de vue et partir d’une représentation complexe de l’algèbre de Clifford C(n)lC avec n = p + q. On veut alors retrouver les représentations des formes réelles C(p,q) à partir de celle(s) de ClC (cette dernière est d’ailleurs unique, à équivalence près, dans le cas pair, puisque l’algèbre est simple). De façon générale, à une forme réelle correspond une involution (une “étoile”) * qui doit satisfaire aux relations *(ab) = *(b) * (a) et ** = 1. Les éléments “réels” sont ceux qui sont hermitiens pour cette involution, c’est à dire, qui sont tels que *a = a. Ainsi, par exemple M(2, I H) est l’ensemble des éléments hermitiens de M(4, lC) pour une étoile particulière.
Au niveau de l’espace vectoriel support d’une représentation de l’algèbre complexifiée, l’existence des trois types de représentations est liée à l’existence, ou non, d’un opérateur c, appelé (en physique surtout) un opérateur de conjugaison de charge, qui est défini comme un opérateur antilinéaire de carré ±1, commutant avec les générateurs γμ de ClC. En d’autres termes c doit être un ClC-isomorphisme de l’espace vectoriel complexe EDirac sur l’espace vectoriel conjugué EDirac (le même espace vectoriel muni de la loi externe conjuguée). Il existe trois cas : Premier cas : c existe et c2 = -1. Dans ce cas le type est quaternionique. L’opérateur c (qui n’est pas unique) correspond à la conjugaison complexe dans le commutant, suivie de la multiplication par un des trois générateurs quaternioniques. Deuxième cas : il n’existe pas de conjugaison de carré -1 mais il existe une conjugaison c de carré 1. Dans ce cas, le type est réel et c correspond à la conjugaison complexe du commutant. Troisième cas : lorsqu’il n’existe pas de conjugaison, le type est complexe.
Si n = p + q est pair, il n’existe qu’une seule représentation de Dirac, puisque ClC est simple.
Si n est impair, nous en avons deux, puisque ClC est somme de deux algèbres simples, mais ces deux représentations ne sont pas fidèles (la somme des deux l’est).
Dans tous les cas, EDirac = lCf où f = 2[n∕2], [n∕2] désignant la partie entière de n∕2. Ceci résulte immédiatement du fait que dimC = 2n.
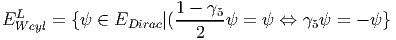
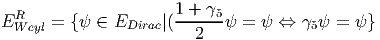
Si n est impair, la restriction de la représentation de Dirac à la sous algèbre C0lC reste irréductible puisque C0lC est simple. L’opérateur γ5 ne permet pas de décomposer un spineur de Dirac (on a déjà γ5ψ = ±1).
Rappelons que Pin(p,q) et Spin(p,q) (le recouvrement de SO(p,q)) sont respectivement obtenus comme sous-ensembles des algèbres C(p,q) et C0(p,q). Les spineurs de Dirac et de Weyl fournissent également des représentations irréductibles des groupes correspondants.
Etant donné une dimension n et un couple d’entiers (p,q) avec n = p + q, on dit qu’il existe des spineurs de Majorana si l’une des deux algèbres C(p,q) ou C(q,p) est de type réel.
L’existence de spineurs de Majorana se lit sur les tables précédentes :
Dans le cas n pair, on a des spineurs de Majorana lorsque la signature (p,q) est telle que p-q = 0, 2ou6modulo8. Exemple : En dimension 4, lorsque la signature est proprement euclidienne, on n’a pas de spineurs de Majorana. Par contre, toujours avec n = 4, on a des spineurs de Majorana, aussi bien lorsque la signature est hyperbolique (un seul temps) que dans le cas neutre (cas (2, 2)).
Dans le cas impair, on a des spineurs de Majorana lorsque p - q = 1ou7modulo8. Ces représentations (cas impair) ne sont pas fidèles.
Soit EDirac l’espace des spineurs de Dirac. Dans le cas n pair, il n’y a pas d’ambiguïté. Dans le cas impair, on peut supposer ϵ2 = 1 (si ce n’est pas le cas, on remplace C(p,q) par C(q,p)). Avec cette dernière hypothèse, on peut toujours trouver un opérateur antilinéaire c. Lorsque c2 = 1, on définit l’espace vectoriel des spineurs de Majorana par
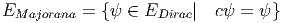
Lorsque (p - q) = 0modulo8, γ5c = cγ5, on peut donc définir les spineurs de Weyl-Majorana de chiralités gauche et droite :
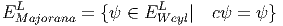
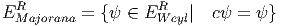
Lorsque cette décomposition est impossible, c’est à dire lorsque γ5c = -cγ5, il faut noter que si ψ ∈ EWeylL, alors c(ψ) ∈ E WeylR
Il existe de nombreuses façons d’écrire les générateurs γμ de C(p,q) sous forme matricielle. En général il n’est pas indispensable d’effectuer un choix quelconque pour faire des calculs : la manipulation formelle des générateurs suffit. Si on tient absolument à utiliser des matrices, il faut noter que l’expression de l’opérateur c, lorsque ce dernier existe, dépend elle aussi de la représentation choisie. Cet opérateur, étant antilinéaire, s’écrira toujours comme la composée de la conjugaison complexe, dont la définition dépend de la représentation, et d’une matrice généralement notée C, dont l’expression dépend aussi de la représentation choisie.
En physique des particules, les spineurs décrivent les particules élémentaires fermioniques les plus “fondamentales” : celles de spin 1∕2. Les spineurs de Dirac décrivent les particules chargées (type électron). L’opérateur de conjugaison de charge associe, à toute particule décrite par le spineur ψ, une autre particule (l’anti-particule de la première) décrite par le spineur c(ψ). Dans le cadre du modèle standard des interactions électrofaibles, les neutrinos sont décrits par des spineurs de Weyl de chiralité gauche (et les anti-neutrinos, bien évidemment, par des spineurs de Weyl de chiralité droite). La nature n’est pas invariante par parité : les neutrinos droits ne semblent pas exister (et, même s’ils existent, ils ont des propriétés très différentes de leurs homologues gauches). Rappelons qu’il n’existe pas de spineurs de Weyl-Majorana en dimension 4 lorsque la signature est euclidienne ou hyperbolique. Il faudrait utiliser une signature (2, 2)… ! Par ailleurs, bien que les spineurs de Majorana soient mathématiquement disponibles en dimension (3, 1), ils n’entrent pas dans la formulation du modèle standard décrivant les particules fondamentales connues.