Une fibration (P,M,π) est un espace fibré principal lorsque les trois conditions suivantes sont satisfaites :
Les trois conditions ci-dessus sont obligatoires pour qu’on puisse parler de fibré principal car nous verrons un peu plus loin des exemples où (1) et (2) sont vérifiées (mais pas (3)) et des exemples où (1) et (3) sont vérifiées (mais pas (2)).
En général, on considère des espaces fibrés principaux à droite, comme ci-dessus, mais il est bien évident qu’on peut également considérer des espaces fibrés principaux à gauche.
Le groupe G (la fibre type) est généralement désigné sous le nom de groupe structural du fibré considéré. Afin d’alléger les notations, nous noterons très simplement l’action de G sur P : Soient z1 ∈ P et g ∈ G, l’image z2 de z1 sous l’action de g sera notée z2 = z1g, ce qui peut être décrit, de façon imagée, par la figure 3.5.
Attention : Parce que G agit sur P, de nombreux physiciens désignent ces
transformations de P dans P (du type z ∈ P z′ = zg,g ∈ G) sous le nom de
transformations de jauge globales et désignent également G lui même sous le nom
de groupe de jauge ; cependant nous réserverons ce dernier vocable (groupe de
jauge) pour le groupe des transformations de jauge locales que nous définirons un
peu plus loin.
z′ = zg,g ∈ G) sous le nom de
transformations de jauge globales et désignent également G lui même sous le nom
de groupe de jauge ; cependant nous réserverons ce dernier vocable (groupe de
jauge) pour le groupe des transformations de jauge locales que nous définirons un
peu plus loin.
La relation z2 = z1g est formellement très semblable à la relation élémentaire
A2 = A1 +  où A1 et A2 désignent deux points d’un espace affine et où
où A1 et A2 désignent deux points d’un espace affine et où  désigne un vecteur de l’espace vectoriel sous-jacent. Les élèves de nos lycées
savent bien qu’on peut “soustraire” deux points en écrivant
désigne un vecteur de l’espace vectoriel sous-jacent. Les élèves de nos lycées
savent bien qu’on peut “soustraire” deux points en écrivant 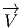 = A2 -A1 (on n’a
pas le droit d’“additionner” deux points !). De la même façon, on pourra écrire
ici g = z1-1z
2, puisque z1g = z2 et que g est bien déterminé par la donnée de z1
et de z2. Notons enfin que l’analogue de la célèbre “relation de Chasles” s’écrit
z1-1z
2 = (z1-1z
3)(z3-1z
2).
= A2 -A1 (on n’a
pas le droit d’“additionner” deux points !). De la même façon, on pourra écrire
ici g = z1-1z
2, puisque z1g = z2 et que g est bien déterminé par la donnée de z1
et de z2. Notons enfin que l’analogue de la célèbre “relation de Chasles” s’écrit
z1-1z
2 = (z1-1z
3)(z3-1z
2).
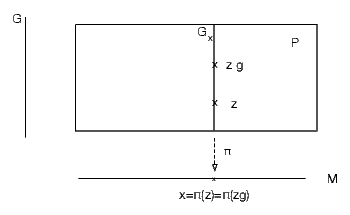
Dans le cas d’un fibré principal, chaque fibre Gx au dessus de x, élément de M est une “copie” du groupe G, mais il s’agit d’une copie au sens topologique (ou différentiable) du terme car l’origine du groupe G (l’élément neutre) est connue mais celle de la fibre Gx ne l’est pas ! Afin de mieux faire sentir le sens de cette importante remarque, considérons l’exemple suivant 3.6

Dans le cas présent, P est un cylindre fini P = M ×S1 où M est un intervalle et S1 désigne le cercle de rayon 1 ; la fibre au dessus de x est un cercle, et ce cercle, comme tous les cercles, est homéomorphe au groupe U(1). Sur ce cercle, tous les points “se valent” et on ne sait pas multiplier un point par un autre. Par contre, si le cercle est marqué par une origine, il devient isomorphe au groupe U(1) et on sait alors multiplier les points (eiθeiα = ei(θ+α)). Le groupe U(1) agit bien sur l’ensemble P ci-dessus en faisant tourner un point quelconque z ∈ P d’un angle θ.
Revenons au cas général d’un fibré principal (P,M,π) de groupe structural G.
Le choix d’une section locale x ∈ U ⊂ M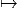 σ(x) ∈ P permet de “marquer une
origine” sur chacune des fibres Gx situées au dessus de l’ouvert U. En
d’autres termes, le choix d’une section locale σ permet d’identifier la fibre
Gx avec le groupe G lui-même. La façon la plus simple d’exprimer ceci
de façon algébrique consiste à montrer qu’à la section locale σ on peut
associer une trivialisation locale ψU définie comme suit : soit z ∈ P,
alors ψU(z) = (x; gσ) où x = π(z) et où gσ désigne l’unique élément de G
défini par z = σ(x)gσ. En effet, z et σ(x) étant dans la même fibre, il
existe un et un seul élément gσ de G permettant de passer de σ(x) à
z ; l’existence et l’unicité de cet élément gσ résulte des axiomes (2) et
(3) de la structure de fibré principal. Une section locale σ définit donc
également une application — que nous noterons encore gσ — de P dans
G ; en d’autres termes, les “composantes” de z ∈ P sont x = π(z) ∈ M
et gσ = gσ(z) ∈ G. La composante x est canoniquement définie par la
structure fibrée et la composante gσ résulte du choix d’une section locale
σ.
σ(x) ∈ P permet de “marquer une
origine” sur chacune des fibres Gx situées au dessus de l’ouvert U. En
d’autres termes, le choix d’une section locale σ permet d’identifier la fibre
Gx avec le groupe G lui-même. La façon la plus simple d’exprimer ceci
de façon algébrique consiste à montrer qu’à la section locale σ on peut
associer une trivialisation locale ψU définie comme suit : soit z ∈ P,
alors ψU(z) = (x; gσ) où x = π(z) et où gσ désigne l’unique élément de G
défini par z = σ(x)gσ. En effet, z et σ(x) étant dans la même fibre, il
existe un et un seul élément gσ de G permettant de passer de σ(x) à
z ; l’existence et l’unicité de cet élément gσ résulte des axiomes (2) et
(3) de la structure de fibré principal. Une section locale σ définit donc
également une application — que nous noterons encore gσ — de P dans
G ; en d’autres termes, les “composantes” de z ∈ P sont x = π(z) ∈ M
et gσ = gσ(z) ∈ G. La composante x est canoniquement définie par la
structure fibrée et la composante gσ résulte du choix d’une section locale
σ.
Il faut enfin noter que le choix d’une section locale permet de définir localement l’action à gauche du groupe G sur P ; en effet, en plus de l’action à droite z ∈ P,k ∈ G → zk = (x; gσ)k = (x; gσk) ∈ P qui ne dépend pas de σ et qui est globalement définie puisqu’elle résulte de la structure d’espace fibré principal, on peut définir localement une action à gauche z ∈ P,k ∈ G → (kz)σ = (x; kgσ) ∈ P, qui dépend de σ.
Supposons que nous ayons fait le choix d’une section locale σ au dessus de
l’ouvert U et d’une section locale τ au dessus de l’ouvert V ; si on fait un choix
de z ∈ P tel que la projection π(z) appartienne à l’intersection U ∩ V , on peut
écrire aussi bien z 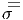 (x; gσ) que z
(x; gσ) que z 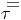 (x; gτ). Il existe donc un élément gστ du
groupe G (et en fait une fonction gστ(x) définie sur U ∩ V ) tel que gσ = gστgτ.
Cette fonction porte le nom de fonction de transition . Ces fonctions de
transition permettent en fait de reconstruire le fibré principal lui-même. On
montre qu’étant donnés un atlas de M et une famille de fonctions de
transition obéissant à une certaine propriété (dite de cocycle) sur les
triples intersections, il est possible de reconstruire l’espace fibré dont on est
parti.
(x; gτ). Il existe donc un élément gστ du
groupe G (et en fait une fonction gστ(x) définie sur U ∩ V ) tel que gσ = gστgτ.
Cette fonction porte le nom de fonction de transition . Ces fonctions de
transition permettent en fait de reconstruire le fibré principal lui-même. On
montre qu’étant donnés un atlas de M et une famille de fonctions de
transition obéissant à une certaine propriété (dite de cocycle) sur les
triples intersections, il est possible de reconstruire l’espace fibré dont on est
parti.
L’exemple qui suit est fondamental, non seulement parce qu’il est mathématiquement important — il est d’ailleurs à l’origine de toute la théorie des espaces fibrés — mais aussi parce qu’il permet de fournir un support à notre intuition géométrique, en particulier dans le cas où l’on s’intéresse à des fibrés principaux (P,M,π) quelconques. L’exemple fondamental étudié ici nous permettra de développer les analogies suivantes :
Soit M une variété différentiable de dimension n. En chaque point x de M nous avons un espace tangent T(M,x) et nous pouvons considérer l’ensemble Gx de tous les repères en x. Un point z de Gx est donc un repère en x, c’est à dire la donnée de n vecteurs indépendants de T(M,x). Soit P = ⋃ x∈MGx l’ensemble de tous les repères de M. Notons π l’application qui, à un repère centré sur x, associe l’origine x elle-même ; il est facile de voir que (P,M,π) est un espace fibré principal de groupe structural GL(n). Il est clair, en effet, que le groupe linéaire GL(n) agit transitivement sur chaque fibre de P : la fibre Gx au dessus de x n’est autre que l’ensemble des repères en x et il est bien évident qu’on peut toujours passer d’un repère z = (zi)i∈{1…n} à un repère z′ = (z′j) au même point x à l’aide d’un élément g = (gji) de GL(n) : (z′ j = zigji). Par ailleurs, le fait que l’ensemble G x des repères en x soit homéomorphe à GL(n) peut se voir de la façon suivante : marquons (choisissons) un repère de référence σ = (σ)i en x ; alors, tout élément g de GL(n) définit un nouveau repère z = σg au même point, mais réciproquement, tout nouveau repère z détermine un et un seul élément g de GL(n) tel que z = σg. On obtient donc une correspondance bi-univoque entre repères en x et éléments de GL(n) ; bien entendu, cette correspondance dépend du choix du repère de référence σ. Il resterait à montrer que cette application est bel et bien continue et à vérifier les conditions de trivialité locale. Le fibré principal P ainsi construit se note parfois FM (pour “Frame bundle of M”) et s’appelle le fibré des repères linéaires sur M. Nous invitons le lecteur à relire la sous-section précédente avec cet exemple en tête ; il est alors clair qu’une section locale n’est autre qu’un repère mobile choisi dans le domaine d’un ouvert et qu’une fonction de transition n’est autre qu’un changement de repère mobile.
Si z′ = zg désigne le repère issus de z par une “rotation” finie g, on pourra écrire ϵα(z) = zXα et interpréter ϵα(z) comme une déplacement infinitésimal du “repère” z à l’aide de la “rotation infinitésimale” Xα.
Pour ne pas alourdir le texte, nous supprimerons les guillemets autour des mots “repère” et “rotation” dans la suite du texte, mais le lecteur devra se souvenir que ces mots désignent respectivement les éléments du fibré principal considéré (qui ne sont pas nécessairement des repères au sens usuel du terme) et les éléments du groupe structural (qui n’est pas nécessairement un groupe de rotations).
 σ(x) ∈ P ;
on a vu qu’une telle section permettait d’identifier la fibre Fx avec
G lui-même en associant au point z ∈ Fx l’élément gσ de G défini
par l’équation z = σ(x)gσ. On a alors non seulement une action de
G à droite mais également une action de G à gauche définie par
k ∈ G,z = (x,gσ) ∈ P
σ(x) ∈ P ;
on a vu qu’une telle section permettait d’identifier la fibre Fx avec
G lui-même en associant au point z ∈ Fx l’élément gσ de G défini
par l’équation z = σ(x)gσ. On a alors non seulement une action de
G à droite mais également une action de G à gauche définie par
k ∈ G,z = (x,gσ) ∈ P z′ = (x,kgσ) ∈ P. Cette action dépend de la
section σ et permet de définir localement des champs fondamentaux
à gauche eα(z) ; ces champs dépendent donc également du choix de
la section σ et, si la chose est nécessaire, on pourra les noter σe
α.
z′ = (x,kgσ) ∈ P. Cette action dépend de la
section σ et permet de définir localement des champs fondamentaux
à gauche eα(z) ; ces champs dépendent donc également du choix de
la section σ et, si la chose est nécessaire, on pourra les noter σe
α.
Un fibré principal (P,M,π) de groupe structural G est trivial si, par définition, P est homéomorphe au produit cartésien M ×G (la projection π étant la projection sur le premier facteur). dans ce cas, il existe plusieurs (en général une infinité de) sections globales puisque toute application différentiable de M dans G définit une section globale : considérer par exemple l’application constante qui, à tout point de M associe l’identité de G. Réciproquement, supposons qu’un fibré principal possède une section globale σ, on peut alors considérer l’application de P dans M × G définie par z → (x,g) avec x = π(z) et g tel que z = σ(x)g ; on fabrique ainsi un homéomorphisme entre P et M × G.
En conclusion, un fibré principal est trivial si et seulement s’il possède une section globale. Lorsque P est trivial, son identification avec M × G résulte, comme on vient de le voir, du choix de la section globale σ ; on écrira simplement P = M × G si cela ne prête pas à confusion. Noter que, dans un tel cas, les champs fondamentaux à droite ϵα et à gauche σe α sont tous deux globalement définis.
Attention : pour des fibrés non principaux (voir plus loin), le fait de posséder une section globale n’est pas suffisant pour assurer la trivialité.
Nous n’aborderons pas le problème de la classification des espaces fibrés, le lecteur interessé devrait consulter [8].
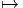 M
permet, comme nous le savons, de projeter les vecteurs de TP sur les
vecteurs de TM, en utilisant l’application tangente π* ; l’application
cotangente, π*, permet, quant à elle, de faire voyager les formes dans
l’autre sens. L’image, par π* d’une forme différentielle sur M est une
forme particulière sur P qu’on appelle une forme basique. On obtient
un homomorphisme injectif d’algèbres différentielles
M
permet, comme nous le savons, de projeter les vecteurs de TP sur les
vecteurs de TM, en utilisant l’application tangente π* ; l’application
cotangente, π*, permet, quant à elle, de faire voyager les formes dans
l’autre sens. L’image, par π* d’une forme différentielle sur M est une
forme particulière sur P qu’on appelle une forme basique. On obtient
un homomorphisme injectif d’algèbres différentielles
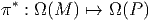
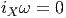
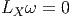
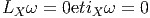
 M du
fibré considéré), notion générale déjà introduite au chapitre 1. Ici
l’ensemble des antécédents de x ∈ M par π n’est autre que la fibre
au dessus du point x. Un champ de vecteurs V ∈ ΓTP est donc dit
projetable si et seulement si π*V z = π*V zg pour tout g ∈ G.
M du
fibré considéré), notion générale déjà introduite au chapitre 1. Ici
l’ensemble des antécédents de x ∈ M par π n’est autre que la fibre
au dessus du point x. Un champ de vecteurs V ∈ ΓTP est donc dit
projetable si et seulement si π*V z = π*V zg pour tout g ∈ G.
Plusieurs propriétés des espaces fibrés (et des connexions) pourraient s’enoncer en utilisant cette notion, que nous n’utiliserons pas explicitement dans la suite.
Nous avons déjà étudié cet exemple en détail en 3.2.3 et nous verrons un peu plus loin divers exemples analogues.
L’espace total Z Z s’écrit donc ici comme réunion de trois fibres. La fibre type est le groupe additif des multiples de 3, noté 3Z Z et l’espace des fibres —la base— possède trois points : Z Z∕3Z Z = {0,1,2} et est un quotient de Z Z. La notation adoptée, pour l’action du groupe structural sur l’espace total Z Z est ici une notation additive et non pas une notation multiplicative (mais cela devrait être assez clair !), ainsi, l’élément 11 de la fibre 2 peut s’obtenir à partir de l’élément -1 de la même fibre sous l’action de 3Z Z en écrivant 11 = -1 + 3 × 4.
Bien évidemment, le groupe U(1) agit, par multiplication à droite, sur l’espace total SU(2) (dans la construction précédente on a choisi U(1) comme sous-groupe de SU(2)). Cette fibration en cercles de S3 est souvent utilisée et porte le nom de “fibration de Hopf” (pour S3).
Avant de généraliser cet exemple, notons que la sphère S3 n’est, en aucun
cas homéomorphe au produit cartésien S2 × S1, ce qui ne l’empêche pas
d’être un fibré en cercles au dessus de S2. En d’autres termes, les deux
espaces fibrés principaux S3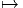 S2 et S2 × S1
S2 et S2 × S1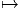 S2 (avec projection
canonique évidente) ont même structure locale —ils sont tous deux fibrés
en cercles au dessus de S2— mais le second est trivial alors que le premier
ne l’est pas.
S2 (avec projection
canonique évidente) ont même structure locale —ils sont tous deux fibrés
en cercles au dessus de S2— mais le second est trivial alors que le premier
ne l’est pas.
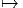 G∕H qui, à tout
élément associe sa classe g = gH, définit une fibration principale.
Tout groupe G est donc ainsi un espace fibré principal au dessus de
G∕H, le groupe structural étant H. Notons que l’espace quotient (la
base du fibré) G∕H n’est généralement pas un groupe, à moins que
H ne soit un sous groupe distingué de G, c’est à dire à moins que les
classes à gauche et à droite ne coïncident. La propriété qui précède est
illustrée par la figure 3.9 et est à l’origine d’une multitude d’exemples
que le lecteur pourra construire en utilisant les données “zoologiques”
concernant les groupes de Lie et les espaces homogènes (voir chapitre
précédent).
G∕H qui, à tout
élément associe sa classe g = gH, définit une fibration principale.
Tout groupe G est donc ainsi un espace fibré principal au dessus de
G∕H, le groupe structural étant H. Notons que l’espace quotient (la
base du fibré) G∕H n’est généralement pas un groupe, à moins que
H ne soit un sous groupe distingué de G, c’est à dire à moins que les
classes à gauche et à droite ne coïncident. La propriété qui précède est
illustrée par la figure 3.9 et est à l’origine d’une multitude d’exemples
que le lecteur pourra construire en utilisant les données “zoologiques”
concernant les groupes de Lie et les espaces homogènes (voir chapitre
précédent). 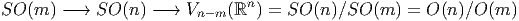
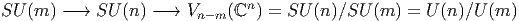
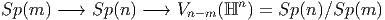
Si x = x0 + ix1 + jx2 + kx3 ∈ I H, alors x = x0 - ix1 - jx2 - kx3, et (x|y) = ∑ xiyi. Comme dans le chapitre précédent, la notation Sp(n) désigne le groupe de Lie compact simplement connexe correspondant à la forme réelle compacte de l’algèbre de Lie complexe Cn. Avec d’autres notations : Sp(n) = U(n, I H) = {u ∈ GL(I H)|(u(x)|u(y)) = (x|y). Le groupe symplectique (non compact) usuel correspondant à la même algèbre de Lie Cn sera généralement plutôt désigné par la notation Sp(2n, I R).
Le cas m = n - 1 mérite une attention particulière puisque nous obtenons les sphères de cette façon.
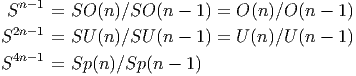
Noter que la même sphère peut être obtenue comme base de plusieurs fibrations différentes de groupes de Lie (trois possibilités si elle est de dimension 4n - 1, deux possibilités si elle est de dimension 2n - 1 et une seule possibilité si elle est de dimension paire). Il existe encore quelques autres possibilités dites “exceptionnelles” et nous y reviendrons plus loin.
Si nous divisons les groupes orthogonaux O(n) ou SO(n) — ou leurs analogues complexes ou quaternioniques — par un sous groupe maximal quelconque, nous obtenons plus généralement les variétés de Grassmann et les fibrations principales correspondantes :
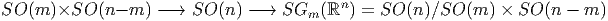
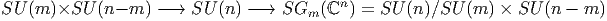
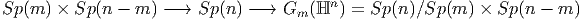
Les Grassmaniennes non orientées réelles et complexes sont
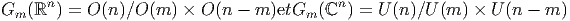
Le cas m = n- 1 mérite également une mention particulière puisque nous obtenons ainsi les espaces projectifs réels (I RPn), complexes (lCPn) et quaternioniques (I HPn).
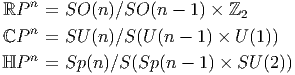
Le lecteur devrait également connaître l’existence des difféomorphismes exceptionnels suivants : lCP1 ~ S2 et I HP1 ~ S4. Une remarque sur les notations : H = S(U(n - 1) × U(1)) désigne un sous groupe maximal de SU(n) ; on écrit quelquefois SU(n - 1) × U(1) pour désigner ce même sous groupe H mais une telle notation est un peu abusive puisque H est en fait en quotient du produit direct de ces deux groupes par un groupe discret (il ne faut pas compter l’unité deux fois !). Les deux objets ont bien évidemment la même algèbre de Lie. Une remarque analogue s’applique au cas symplectique (par ailleurs on se rappelle que Sp(1) et SU(2) sont isomorphes, ce qui explique l’apparition de ce dernier dans le tableau précédent).
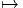 GL ~ G et GLGR
GL ~ G et GLGR GR ~ G qui définissent deux autres
fibrés principaux (cette fois-ci, la structure de groupe passe au
quotient).
GR ~ G qui définissent deux autres
fibrés principaux (cette fois-ci, la structure de groupe passe au
quotient).
 et que G est isomorphe au groupe quotient
et que G est isomorphe au groupe quotient
 |H où H est un sous groupe discret (distingué) du centre de G
isomorphe au groupe d’homotopie π1(G). On se retrouve donc dans
la situation considérée précédemment d’une fibration de
|H où H est un sous groupe discret (distingué) du centre de G
isomorphe au groupe d’homotopie π1(G). On se retrouve donc dans
la situation considérée précédemment d’une fibration de  au dessus
de G =
au dessus
de G =  |H avec groupe structural (fibre type) H, à ceci près que
le groupe H est ici un groupe discret admettant une interprétation
topologique particulière et que le quotient G est non seulement un
espace homogène, mais est lui-même un groupe. Plus généralement
d’ailleurs, tout sous groupe K ⊂ H ~ π1(G) définit un revêtement
|H avec groupe structural (fibre type) H, à ceci près que
le groupe H est ici un groupe discret admettant une interprétation
topologique particulière et que le quotient G est non seulement un
espace homogène, mais est lui-même un groupe. Plus généralement
d’ailleurs, tout sous groupe K ⊂ H ~ π1(G) définit un revêtement
 ∕K qui est un fibré principal au dessus de G =
∕K qui est un fibré principal au dessus de G =  ∕H avec fibres
H|K (c’est bien un groupe puisque H est abélien) ; ce revêtement
n’est pas universel puisque son π1 est égal à K. Tout ceci est presque
intuitif si on se représente ces fibrations par des figures telles que 3.10.
∕H avec fibres
H|K (c’est bien un groupe puisque H est abélien) ; ce revêtement
n’est pas universel puisque son π1 est égal à K. Tout ceci est presque
intuitif si on se représente ces fibrations par des figures telles que 3.10.
Soit H un sous groupe de Lie d’un groupe de Lie G et supposons que H soit
isomorphe au produit H1 × H2 de deux groupes de Lie. On peut alors considérer
H1 (en fait H1 × Identité) comme sous groupe de G et on a une projection
G∕H1 G∕(H1 × H2) de fibre H2. L’action de H2 (à droite) sur G∕H1 est bien
définie car H1 et H2 commutent, et donc (gH1)h2 = (gh2)H1 lorsque h2
appartient à H2. Vu la diversité des cas à considérer nous n’énoncerons aucun
résultat précis dans ce cas. Néanmoins nous énoncerons les trois remarques
suivantes :
G∕(H1 × H2) de fibre H2. L’action de H2 (à droite) sur G∕H1 est bien
définie car H1 et H2 commutent, et donc (gH1)h2 = (gh2)H1 lorsque h2
appartient à H2. Vu la diversité des cas à considérer nous n’énoncerons aucun
résultat précis dans ce cas. Néanmoins nous énoncerons les trois remarques
suivantes :
 K\G∕H ne définit en général pas une fibration
principale, ni même une fibration, car le type topologique des fibres
(ou même la cardinalité) peut varier d’un point à l’autre de la base.
K\G∕H ne définit en général pas une fibration
principale, ni même une fibration, car le type topologique des fibres
(ou même la cardinalité) peut varier d’un point à l’autre de la base.Afin de conclure cette sous section consacrée aux exemples par un théorème précis concernant les fibrations principales d’espaces homogènes, nous considérons maintenant le cas suivant.
Soit H un sous groupe de Lie du groupe de Lie G et soit N son normalisateur dans G. On rappelle que N = {n ∈ G|nH = Hn} ;end’autrestermes, N est le plus grand sous groupe de G dans lequel H est un sous groupe normal (on dit aussi sous groupe distingué). H étant normal dans N, il s’ensuit que les classes à gauche et à droite de N par rapport à H coïncident (voir ci-dessus la définition de N) et que l’espace homogène N|H = N∕H = H\N possède une structure de groupe. Par ailleurs, N agit à droite sur G∕H : soit gH ∈ G∕H et n ∈ N ; alors gHn = gnH ∈ G∕H. Cette action n’est pas fidèle car les éléments de H lui-même n’agissent pas : si h ∈ H, alors gHh = gH. Le fait de quotienter N par H rend précisément cette action fidèle. On peut se représenter les actions de G à gauche de G∕H et de N|H, à droite de G∕H par le schéma :
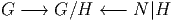
Ce type de fibration principale est également à l’origine d’une multitude d’exemples. Les fibrations de Hopf des sphères au dessus des espaces projectifs réels, complexes ou quaternioniques sont d’ailleurs de ce type. En effet, on a
| G = SO(n) | H = SO(n - 1) | N = SO(n - 1) × Z Z2 | N|H = Z Z2 |
| G∕H = Sn-1 | G∕N = I RPn |
| G = SU(n) | H = SU(n - 1) | N = SU(n - 1) × U(1) | N|H = U(1) |
| G∕H = S2n-1 | G∕N = lCPn-1 |
| G = Sp(n) | H = Sp(n - 1) | N = Sp(n - 1) × SU(2) | N|H = SU(2) |
| G∕H = S4n-1 | G∕N = I HPn |
et on peut illustrer les fibrations correspondantes par la figure 3.12
On se souvient aussi que Z2 ≡ S0, U(1) ≡ S1 et SU(2) ≡ S3 ; ainsi les trois fibres types représentées sur la figure 3.12 sont non seulement des groupes, mais aussi des sphères.
Le lecteur pourra fabriquer aisément d’autres exemples de ce type en choisissant, pour tout groupe G donné, un sous groupe H qui ne soit pas trop “gros” (de façon à ce que N|H ne soit pas trop trivial). Voici un dernier exemple de ce type qui utilise les groupes de Lie exceptionnels : G = E8, H = E6 , N = (E6 × SU(3))∕Z Z3, N|H = SU(3)∕Z Z3.
Il existe des fibrations exceptionnelles des sphères et des espaces projectifs qui
ne sont pas liées aux inclusions de groupes unitaires, orthogonaux ou
symplectiques (forme compacte) c’est à dire aux structures réelles, complexes ou
quaternioniques. Certaines de ces fibrations sont liées à l’existence de
l’“algèbre” non-associative des octaves de Cayley  (octonions). On sait que
pour n = 1, 2, 4, 8 (et ce sont les seules valeurs possibles), il existe une
opération bilinéaire I Rn × I Rn
(octonions). On sait que
pour n = 1, 2, 4, 8 (et ce sont les seules valeurs possibles), il existe une
opération bilinéaire I Rn × I Rn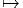 I Rn sans diviseurs de zéro (c’est à dire que
a × b = 0 ⇒a = 0oub = 0), conduisant à la définition des corps I R, lC, I H et des
octaves
I Rn sans diviseurs de zéro (c’est à dire que
a × b = 0 ⇒a = 0oub = 0), conduisant à la définition des corps I R, lC, I H et des
octaves  .
.
Certaines des fibrations mentionnées ici ne sont pas des fibrations principales (en particulier la fibre type n’est pas un groupe) mais elles y ressemblent beaucoup (on sait que la sphère S7, par exemple, est presque un groupe…) Nous donnons ici une liste de fibrations qui sont à la fois intéressantes et célèbres (la fibration de Hopf exceptionnelle de S15 !) bien qu’elles ne s’inscrivent pas logiquement toutes dans cette section puisqu’il ne s’agit pas toujours de fibrations principales. Nous ne les utiliserons pas dans la suite et ne les mentionnons que pour des raisons culturelles, en espérant que le lecteur pourra y retourner (soit-dit en passant, il reste à étudier de nombreux problèmes intéressants concernant ces objets).
