2.4 Champs de vecteurs fondamentaux
2.4.1 Cas d’un groupe de Lie agissant sur une variété
- On se donne un groupe de Lie G et une action à gauche (supposée
différentiable) de G sur une variété M. Il y a, au moins, trois façons de
considérer cette action :
- Comme une application de G × M dans M :
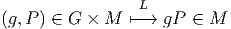
- Comme la donnée, pour tout point P dans M, d’une application
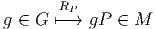
- Comme la donnée, pour tout élément g du groupe G, d’une
application
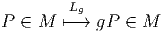
Attention : Une action à gauche fournit une application notée Lg quand on
gèle l’élément g du groupe mais fournit une application notée
RP quand on gèle le point P. L’application Lg n’est autre que
celle qui nous a permis précédemment de définir l’action d’un
groupe sur un ensemble. Notons que Lg = L(g,⋅). C’est en fait
surtout le point de vue 2 qui nous intéresse ici et nous allons donc
étudier l’application RP = L(⋅,P). L’application RP étant supposée
différentiable, nous pouvons considérer sa différentielle notée suivant les
auteurs, RP *, TRP ou simplement dRP . Comme on le sait (voir la
première partie de cet ouvrage), dRP est une application linéaire
de l’espace tangent T(G,g) dans l’espace tangent T(M,gP) dont
l’expression, relativement à un couple de repères mobiles dans G et M
s’écrit à l’aide de la matrice jacobienne. Si on choisit alors g = e
(l’élément neutre de G), on obtient ainsi une application linéaire
T(G,e) T(M,P) qu’on devrait noter (dRP )g=e mais que nous
préférons ne pas baptiser du tout. L’important est d’observer qu’on
obtient ainsi, pour tout vecteur X appartenant à T(G,e) un vecteur
noté XL(P) appartenant à T(M,P). Puisque cette application
existe pour tout P de M, on obtient donc un champ de vecteurs
P ∈ M
T(M,P) qu’on devrait noter (dRP )g=e mais que nous
préférons ne pas baptiser du tout. L’important est d’observer qu’on
obtient ainsi, pour tout vecteur X appartenant à T(G,e) un vecteur
noté XL(P) appartenant à T(M,P). Puisque cette application
existe pour tout P de M, on obtient donc un champ de vecteurs
P ∈ M XL(P) ∈ T(M,P). On dit que XL est le champ de vecteurs
fondamental gauche associé à l’élément X de l’espace tangent à G en
l’identité.
XL(P) ∈ T(M,P). On dit que XL est le champ de vecteurs
fondamental gauche associé à l’élément X de l’espace tangent à G en
l’identité.
- Nous verrons un peu plus loin que l’algèbre de Lie de G, que nous avons
précédemment définie de façon élémentaire à l’aide de la fonction
exponentielle, peut s’identifier, en tant qu’espace vectoriel à l’espace
tangent à G en l’identité : Lie(G) = T(G,e). En anticipant légèrement,
nous voyons donc qu’à tout élément X de Lie(G) on peut associer un
champ de vecteurs XL sur M. Résumons cette construction simple et
fondamentale par le diagramme suivant :
- Le champ fondamental gauche associé à X ∈ LieG se note, soit XL(P)
comme ci-dessus, soit, encore plus simplement
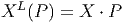 Pour rendre cette notation naturelle, il suffit de développer l’exponentielle
dans l’écriture
Pour rendre cette notation naturelle, il suffit de développer l’exponentielle
dans l’écriture
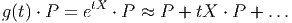 et
ne garder que les termes du premier ordre. Ainsi XL(P) = X.P = d
dt(g(t).P)|t=0.
et
ne garder que les termes du premier ordre. Ainsi XL(P) = X.P = d
dt(g(t).P)|t=0.
- Tout ce que nous avons décrit depuis le début de cette section consacrée à
l’étude des champs fondamentaux supposait donnée une action
à gauche de G sur M. Nous obtenons des notions analogues en
supposant que G agit à droite sur M. En particulier, lorsque M = G,
nous pouvons aussi bien considérer l’action à gauche que l’action à
droite du groupe sur lui-même, et donc, de la même façon que nous
avons construit des champs fondamentaux gauche, nous pouvons
également construire, pour tout élément X de Lie(G) = T(G,e), un
champ de vecteurs fondamentaux droit (le champ fondamental
droit
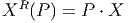 associé à X).
associé à X).
- Certains auteurs désignent les champs fondamentaux sous le nom de
champs de Killing. Pour nous, les champs de Killing sont des champs
fondamentaux particuliers, ceux associés à l’action d’un groupe agissant
par isométries sur une variété riemannienne.
2.4.2 Exemple : le groupe euclidien agissant sur le plan I R2
Le groupe euclidien E(2) agit sur le plan affine M = I R2 par composition de
translations et de rotations autour de l’origine (c’est un produit semi-direct du
groupe des rotations U(1) par le groupe des translations I R2). Une carte (qui est
d’ailleurs globale) de I R2 est définie par les coordonnées (x,y) relatives à un
repère du plan. L’action du groupe euclidien s’écrit
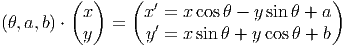 Noter qu’un élément g du groupe euclidien peut s’écrire à l’aide de la carte
g → (θ,a,b) ∈ I R3 ; G est un groupe de Lie de dimension 3. La différentielle de
l’application
Noter qu’un élément g du groupe euclidien peut s’écrire à l’aide de la carte
g → (θ,a,b) ∈ I R3 ; G est un groupe de Lie de dimension 3. La différentielle de
l’application
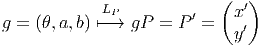 s’écrit
s’écrit
![( )
∂x′∕∂θ ∂x ′∕∂a ∂x′∕∂b
[dLP ]g= (θ,a,b) = ′ ′ ′
∂y ∕∂θ ∂y ∕∂a ∂y ∕∂b](source260x.png) En
prenant g = e = (0, 0, 0), il vient [dLP ]e =
En
prenant g = e = (0, 0, 0), il vient [dLP ]e = 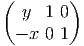 . Grâce à l’utilisation de
quelques abus de notations évidents, nous voyons que
. Grâce à l’utilisation de
quelques abus de notations évidents, nous voyons que
2.4.3 Un cas particulier fondamental : le groupe G agissant sur lui-même
par translations à gauche et à droite
- Nous considérons maintenant le cas où G opère sur M = G lui
même (g,k ∈ G et P ∈ G). Comme nous le savons, il est possible
de considérer deux actions : l’une à gauche g → g ⋅ P et l’autre
à droite k → P ⋅ k. En conséquence, nous avons aussi des champs
fondamentaux à gauche XL et des champs fondamentaux à droite XR.
Soit X ∈ LieG, alors
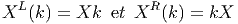 Notons aussi que
Notons aussi que
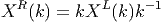
- Les deux actions commutent : (gP)k = g(Pk). Elles commutent
donc aussi infinitésimalement, (XLY R - Y RXL)(k) = X(kY ) -
(Xk)Y = 0. D’où
![L R
[X ,Y ] = 0](source276x.png)
- La propriété XL(g)k = XL(gk) caractérise l’invariance de XL (champ
résultant d’une action à gauche) lorsqu’on le multiplie à droite par
k. On peut donc dire que le champ fondamental gauche XL est un
champ invariant à droite . Attention : Un champ fondamental gauche
est invariant à droite et un champ fondamental droit est invariant à
gauche. Attention, le champ invariant à gauche associé à X se note
XR.
- Soit X ∈ Lie(G). Lorsque t varie, l’élément g(t) = etX décrit une
courbe dans le groupe G et le vecteur tangent à l’origine de cette
courbe est donné par dg(t)
dt |t=0 = X. Inversement, à tout élément X de
T(G,e) on peut associer une courbe à un paramètre g(t) = etX (en fait
il s’agit d’un groupe à un paramètre puisque g(t1 + t2) = g(t1)g(t2)).
On peut ainsi identifier Lie(G), en tant qu’espace vectoriel, et défini
comme précédemment à l’aide de la fonction exponentielle, avec
l’espace tangent en l’identité du groupe G :
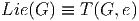
- Un champ fondamental droit XR est parfaitement caractérisé — que
M = G ou non — par X ∈ T(G,e) c’est à dire par un élément
de l’espace tangent à l’identité du groupe G. Dans le cas où M =
G, cependant, la correspondance entre champs fondamentaux droits
(champs invariants à gauche) et éléments de T(G,e) est bijective
(kX = kY,k ∈ G implique X = Y ). Notons que si dimG = n, alors
dimT(G,e) = n et la dimension de l’espace des champs de vecteurs
invariants à gauche est encore n, alors que la dimension de l’espace de
tous les champs de vecteurs est infinie.
- Par ailleurs, on vient de voir que la correspondance entre T(G,e) et
l’ensemble des champs de vecteurs invariants à gauche (par exemple)
était bijective. En effet XR(g) est parfaitement caractérisé par X =
XR(e) puisque XR(g) = g.X. Notons ΓG(TG) l’ensemble de ces
champs de vecteurs. On peut donc identifier Lie(G) avec ΓG(TG) :
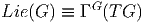 Une autre façon de définir l’algèbre de Lie d’un groupe de Lie G est
donc de la définir comme espace des champs de vecteurs invariants à
gauche sur un groupe de Lie. Le commutateur dans l’algèbre de Lie (le
crochet de Lie) est alors défini simplement comme commutateur des
champs de vecteurs ; il faut évidemment montrer que le commutateur
de deux champs de vecteurs invariants à gauche est encore invariant
à gauche :
Une autre façon de définir l’algèbre de Lie d’un groupe de Lie G est
donc de la définir comme espace des champs de vecteurs invariants à
gauche sur un groupe de Lie. Le commutateur dans l’algèbre de Lie (le
crochet de Lie) est alors défini simplement comme commutateur des
champs de vecteurs ; il faut évidemment montrer que le commutateur
de deux champs de vecteurs invariants à gauche est encore invariant
à gauche :
![[XR, Y R] = [X,Y ]R](source279x.png) Cette propriété résulte de ce qui précède.
Cette propriété résulte de ce qui précède.
- On pourrait bien sur penser à utiliser les champs invariants à
droite pour définir l’algèbre de Lie, cependant (noter le signe), le
commutateur des champs invariants à droite conduit à la relation
(exercice !)
![[XL, Y L] = - [X, Y ]L](source280x.png)
A titre d’exercice (ou d’illustration), vérifions ces propriétés générales dans le
cadre de SL(2, lC).
Les générateurs (représentation fondamentale) sont donnés par
les actions à droite et à gauche sont données par :
X+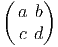 = = 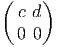 | , | 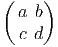 X+ = X+ = 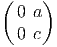 |
X-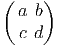 = = 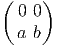 | , | 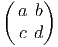 X- = X- = 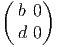 |
X3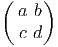 = = 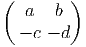 | , | 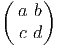 X3 = X3 = 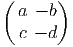 |
| |
Notez que les générateurs X± et X3 agissent par dérivations. En effet, les
actions classiques (droite et gauche) ci-dessus peuvent aussi être écrites à l’aide
des opérateurs différentiels suivants :
| X+L = c ∂_
∂a + d ∂_
∂b | , | X+R = a ∂_
∂b + c ∂_
∂d |
| X-L = a ∂_
∂c + b ∂_
∂d | , | X-R = b ∂_
∂a + d ∂_
∂c |
| X3L = a ∂_
∂a + b ∂_
∂b - c ∂_
∂c - d ∂_
∂d | , | X3R = a ∂_
∂a - b ∂_
∂b + c ∂_
∂c - d ∂_
∂d |
Il est alors facile de vérifier explicitement que, par exemple,
![[X3, X+-] = +2X+,- [XR3 ,XR+] = +2XR+, [XL3,XL+ ] = - 2XR+](source296x.png)
2.4.4 L’action adjointe de G
Le groupe G agit sur lui-même par multiplications à droite et à gauche, comme
nous l’avons vu plus haut, mais également par l’application adjointe. Soit g un
élément de G, on définit :
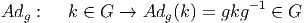 Cette action n’est pas fidèle en général car les éléments du centre C n’agissent
pas. Le groupe G|C qu’on désigne sous le nom de groupe adjoint ou groupe des
automorphismes intérieurs agit, bien sur, de façon fidèle. L’application
tangente à Adg, au point k, envoie T(G,k) dans T(G,gkg-1). Si on prend
alors k = e (l’élément neutre), on voit que l’application tangente, notée
adg = (d(Adg))k=e envoie T(G,e) dans T(G,gg-1 = e), c’est à dire Lie(G)
dans Lie(G). Posant k(t) = etX, on voit que ad
g(X) = d
dt(getXg-1)
|t=0 et
donc
Cette action n’est pas fidèle en général car les éléments du centre C n’agissent
pas. Le groupe G|C qu’on désigne sous le nom de groupe adjoint ou groupe des
automorphismes intérieurs agit, bien sur, de façon fidèle. L’application
tangente à Adg, au point k, envoie T(G,k) dans T(G,gkg-1). Si on prend
alors k = e (l’élément neutre), on voit que l’application tangente, notée
adg = (d(Adg))k=e envoie T(G,e) dans T(G,gg-1 = e), c’est à dire Lie(G)
dans Lie(G). Posant k(t) = etX, on voit que ad
g(X) = d
dt(getXg-1)
|t=0 et
donc
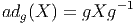
2.4.5 Exemple : l’algèbre de Lie du groupe euclidien
Nous avons déjà fait agir le groupe euclidien G (éléments g = (θ,a,b)) sur
l’espace affine I R2. Nous allons maintenant faire agir G sur lui-même, à
droite.
Soit P ∈ G. On considère l’application
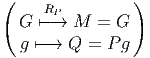 ce
qui, avec des coordonnées, s’écrit
ce
qui, avec des coordonnées, s’écrit
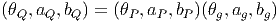 soit, explicitement
soit, explicitement
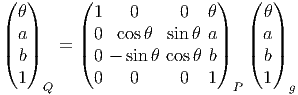 La
différentielle de RP , c’est à direl’application tangente est égale à
La
différentielle de RP , c’est à direl’application tangente est égale à
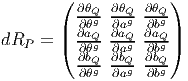 On choisit, comme base de T(G,e) la base Xθ(e) =
On choisit, comme base de T(G,e) la base Xθ(e) =  , Xa(e) =
, Xa(e) = 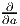 ,
Xb(e) =
,
Xb(e) = 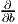 .
.
On calcule dRP 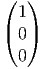 =
= 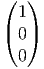 , dRP
, dRP 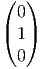 =
= 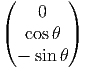 , dRP
, dRP  =
= 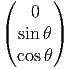 .
.
La base correspondante de LieG ≡ ΓG(TG) est donc
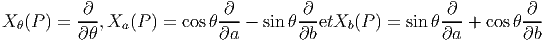
Nous laissons au lecteur le soin de vérifier les relations de commutation
![[X θ,Xa ] = - Xb, [Xθ,Xb ] = +Xa et [Xa, Xb ] = 0](source313x.png)
2.4.6 Exemple : champs invariants sur SU(2)
Le groupe SU(2) est difféomorphe à la sphère S3. Pour le voir, il suffit d’écrire un
élément g de SU(2) comme une matrice 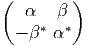 , obéissant à la condition
g† = g-1. Alors, detg†g = 1, c’est à dire
, obéissant à la condition
g† = g-1. Alors, detg†g = 1, c’est à dire
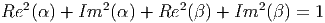 On
obtient ainsi l’équation cartésienne d’une 3-sphère. On peut donc se représenter
visuellement SU(2) comme une sphère dotée d’une structure multiplicative (non
commutative d’ailleurs). Attention, il ne faudrait pas se laisser abuser par cet
exemple : seules les sphères S0 = Z Z
2, S1 = U(1) et S3 = SU(2) sont des groupes
(et S7 est “presque” un groupe). Ces particularités des dimensions 0, 1, 3, 7 sont
liées à l’existence des algèbres de division suivantes : les corps I R (les réels), lC
(les complexes), I H (les quaternions) et les octaves de Cayley (octonions)
On
obtient ainsi l’équation cartésienne d’une 3-sphère. On peut donc se représenter
visuellement SU(2) comme une sphère dotée d’une structure multiplicative (non
commutative d’ailleurs). Attention, il ne faudrait pas se laisser abuser par cet
exemple : seules les sphères S0 = Z Z
2, S1 = U(1) et S3 = SU(2) sont des groupes
(et S7 est “presque” un groupe). Ces particularités des dimensions 0, 1, 3, 7 sont
liées à l’existence des algèbres de division suivantes : les corps I R (les réels), lC
(les complexes), I H (les quaternions) et les octaves de Cayley (octonions)
 .
.
Revenons à la sphère S3 qu’on peut donc identifier avec le groupe de Lie
SU(2). Posons Xi = i∕2σi, où les σi sont les matrices de Pauli (section 2.2.2). On
peut paramétriser un point quelconque g par trois angles d’Euler ψ,θ,ϕ en
écrivant
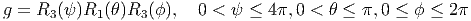 Ri(x) = exp(tXi) est une rotation d’angle x autour de l’axe i. On considère, dans
SU(2) les courbes obtenues par translation à droite, Di(t) = gRi(t) et nous
notons XiR(g) les champs fondamentaux à droite correspondants (les champs
invariants à gauche). En terme du repère naturel associé aux coordonnées
d’Euler, on obtient le repère mobile :
Ri(x) = exp(tXi) est une rotation d’angle x autour de l’axe i. On considère, dans
SU(2) les courbes obtenues par translation à droite, Di(t) = gRi(t) et nous
notons XiR(g) les champs fondamentaux à droite correspondants (les champs
invariants à gauche). En terme du repère naturel associé aux coordonnées
d’Euler, on obtient le repère mobile :
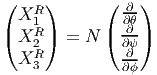 avec
avec
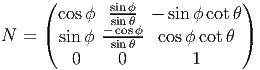 Les
relations de commutation s’écrivent
Les
relations de commutation s’écrivent
![[XR1 ,XR2 ] = - XR3 etc](source319x.png) Le
corepère mobile correspondant {XiR} (le dual du repère mobile {X
iR}) est donné
par
Le
corepère mobile correspondant {XiR} (le dual du repère mobile {X
iR}) est donné
par
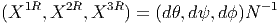
On peut aussi considérer les courbes Gi(t) = Ri(t)g obtenues par translation à
gauche. L’expression des champs de vecteurs invariants à droite XiL (et des
formes correspondantes XiL) s’exprime à l’aide des formules précédentes en
interchangeant simplement partout les coordonnées ϕ et ψ. Les relations de
commutation s’écrivent alors
![[XL1 ,XL2 ] = +XL3 etc](source321x.png) et
on vérifie que
et
on vérifie que
![R L
[X i ,Xj ] = 0](source322x.png)
2.4.7 Une remarque sur les constantes de structure
Soit G un groupe de Lie et choisissons une base Xα dans son algèbre de Lie,
ensemble que nous identifions, en tant qu’espace vectoriel, avec l’espace
tangent T(G,e). Les vecteurs Xα déterminent, comme nous l’avons vu, des
champs de vecteurs invariants à gauche Xα(⋅). L’espace de ces champs de
vecteurs étant, comme on le sait, de dimension finie et étant lui-même
identifiable à l’algèbre de Lie de G, on peut écrire, en tout point P de
G,
 = fαγβ(P )X γ(P)](source323x.png) On
voit qu’on a ainsi obtenu un repère mobile global (les {Xα(P)}) pour lequel les
fonctions de structure sont les fαβγ(P). En fait, ces f
αβγ(P) sont des
constantes : elles ne dépendent pas de P ∈ G. Ceci résulte du fait que le
commutateur de deux champs invariants à gauche est lui-même un champ
invariant à gauche.
On
voit qu’on a ainsi obtenu un repère mobile global (les {Xα(P)}) pour lequel les
fonctions de structure sont les fαβγ(P). En fait, ces f
αβγ(P) sont des
constantes : elles ne dépendent pas de P ∈ G. Ceci résulte du fait que le
commutateur de deux champs invariants à gauche est lui-même un champ
invariant à gauche.
Rappelons que, pour une variété différentiable quelconque, les fonctions de
structure d’un repère mobile dépendent généralement du point où elles sont
évaluées ; par contre, on voit ici que, lorsque cette variété est un groupe de Lie
et que le repère mobile choisi est un champ de vecteurs invariant à gauche, ces
fonctions de structure fαβγ sont des constantes de structure : elles ne
dépendent que de la base choisie dans T(G,e) et non du point P où elles sont
calculées.
En utilisant des champs invariants à droite, on pourrait mener une discussion
analogue, c’est à dire, en particulier, associer à toute base {Xα} de T(G,e) un
repère mobile global constitué de champs invariants à droite XL(g) = Xg et
obtenir des constantes de structure gαβγ = -f
αβγ.
2.4.8 La forme de Maurer-Cartan
- Il existe en fait deux formes de Maurer-Cartan : l’une est “gauche”
et l’autre est “droite”. Tout le monde utilisant des champs invariants
à gauche pour définir l’algèbre de Lie, on parle alors de “la” forme de
Maurer-Cartan.
- La forme de Maurer-Cartan θ est une forme au sens généralisé du
mot. En effet, elle est à valeurs, non pas dans le corps des réels (ou
des complexes) mais dans une algèbre de Lie. Son rôle est de ramener
les champs invariants (à gauche) à l‘origine : soit Xα(g) un champ
invariant à gauche, on définit θg par
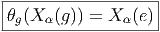 En notant {θα(g)} la base duale, au point g de G de la base {X
α(g)}
et en notant simplement Xα = Xα(e), on voit que
En notant {θα(g)} la base duale, au point g de G de la base {X
α(g)}
et en notant simplement Xα = Xα(e), on voit que
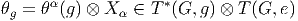 en effet,
en effet,
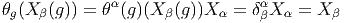 L’application θg va de T(G,g) dans T(G,e). La forme de Maurer-Cartan
elle-même θ = θα(⋅) ⊗ X
α, qu’on peut simplement noter θαX
α, va de
TG dans LieG = T(G,e). En résumé, θ ∈ Ω1(G,LieG).
L’application θg va de T(G,g) dans T(G,e). La forme de Maurer-Cartan
elle-même θ = θα(⋅) ⊗ X
α, qu’on peut simplement noter θαX
α, va de
TG dans LieG = T(G,e). En résumé, θ ∈ Ω1(G,LieG).
Si u ∈ TG, c’est à dire que u est un vecteur en un certain point g,
on peut, a priori décomposer u sur une base de champs invariants
à gauche au point g : u = uαX
α(g). On sait que θ(u) est alors
l’élément de l’algèbre de Lie (identifiée ici avec T(G,e)) égal à
θ(u) = uαX
α(e) = uαX
α. Puisque θ = θαX
α, on définit dθ = dθαX
α
(rappelons que Xα ≡ Xα(e)), mais on sait que, pour un repère mobile
quelconque (voir chapitre précédent), on a dθα + 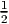 fβγαθβθγ = 0 où
les fβγα sont les fonctions de structure du repère mobile ; ici les
“fonctions de structure” sont les constantes de structure. Pour deux
formes ω et σ à valeurs dans une algèbre de Lie (ω = ωαX
α et
σ = σαX
α) on définit le crochet
fβγαθβθγ = 0 où
les fβγα sont les fonctions de structure du repère mobile ; ici les
“fonctions de structure” sont les constantes de structure. Pour deux
formes ω et σ à valeurs dans une algèbre de Lie (ω = ωαX
α et
σ = σαX
α) on définit le crochet
![[ω ∧ σ ] = [ωαX α ∧ σβX β ] = ω α ∧ ω β[X α,X β] = ω α ∧ σ βfγαβX γ](source328x.png) Ainsi donc l’équation de structure de Maurer-Cartan s’écrit
Ainsi donc l’équation de structure de Maurer-Cartan s’écrit
![|-----------------|
|dθ + 12[θ ∧ θ] = 0 |
------------------](source329x.png)
- Attention aux facteurs 1∕2 et aux notations : la présence du [,]
autour du symbole ∧ est indispensable dans la définition de [ω∧σ] et
on voit que le crochet, en ce sens, d’une p-forme à valeurs dans LieG
avec une q-forme du même type est une (p + q)-forme à valeurs dans
LieG. Prenons de nouveau ω et σ dans Ω1(G,LieG) et évaluons-les
sur des vecteurs u et v : ω(u) = ωα(u)X
α, σ(v) = σβ(v)X
β. On peut
aussi définir
 = [ω (u),σ(v)]](source330x.png) Alors [ωα(u)X
α,σβ(v)X
β] = ωα(u)σβ(v)[X
α,Xβ] = ωα(u)σβ(v)f
αβγX
γ,
mais par ailleurs, ωα∧ωβf
αβγX
γ(u,v) =
Alors [ωα(u)X
α,σβ(v)X
β] = ωα(u)σβ(v)[X
α,Xβ] = ωα(u)σβ(v)f
αβγX
γ,
mais par ailleurs, ωα∧ωβf
αβγX
γ(u,v) = 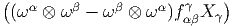 (u,v) =
2ωα(u)ωβ(v)f
αβγX
γ Ainsi [ω ∧ ω](u,v) = 2[ω,ω](u,v) et l’équation
de Maurer-Cartan peut s’écrire également sous la forme
(u,v) =
2ωα(u)ωβ(v)f
αβγX
γ Ainsi [ω ∧ ω](u,v) = 2[ω,ω](u,v) et l’équation
de Maurer-Cartan peut s’écrire également sous la forme
![dθ + [θ,θ] = 0](source332x.png) On peut utiliser indifféremment le crochet [ ∧] ou le crochet [,] mais
ils diffèrent par des facteurs numériques. Par ailleurs, de nombreux
auteurs désignent [ ∧] par [ , ] !
On peut utiliser indifféremment le crochet [ ∧] ou le crochet [,] mais
ils diffèrent par des facteurs numériques. Par ailleurs, de nombreux
auteurs désignent [ ∧] par [ , ] !
- La forme de Maurer-Cartan ci-dessus, définie à l’aide de champs
fondamentaux à droite (c’est à dire à l’aide de champs invariants à
gauche) est celle qui est le plus utilisée. Il ne faut pas oublier qu’“A
travers le miroir” existe une forme analogue, définie à partir des
champs invariants à droite. Notons ω la forme de Maurer-Cartan “à
droite”. Par une méthode analogue à celle qui précède, on montre que
ω satisfait à l’équation de structure
![1
dω - --[ω ∧ ω ] = 0
2](source333x.png)
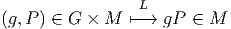
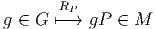
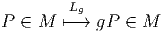
 T(M,P) qu’on devrait noter (dRP )g=e mais que nous
préférons ne pas baptiser du tout. L’important est d’observer qu’on
obtient ainsi, pour tout vecteur X appartenant à T(G,e) un vecteur
noté XL(P) appartenant à T(M,P). Puisque cette application
existe pour tout P de M, on obtient donc un champ de vecteurs
P ∈ M
T(M,P) qu’on devrait noter (dRP )g=e mais que nous
préférons ne pas baptiser du tout. L’important est d’observer qu’on
obtient ainsi, pour tout vecteur X appartenant à T(G,e) un vecteur
noté XL(P) appartenant à T(M,P). Puisque cette application
existe pour tout P de M, on obtient donc un champ de vecteurs
P ∈ M XL(P) ∈ T(M,P). On dit que XL est le champ de vecteurs
fondamental gauche associé à l’élément X de l’espace tangent à G en
l’identité.
XL(P) ∈ T(M,P). On dit que XL est le champ de vecteurs
fondamental gauche associé à l’élément X de l’espace tangent à G en
l’identité.
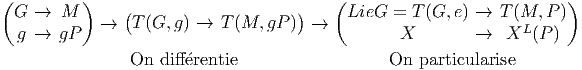
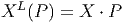
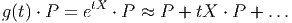
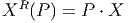
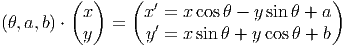
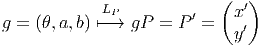
![( )
∂x′∕∂θ ∂x ′∕∂a ∂x′∕∂b
[dLP ]g= (θ,a,b) = ′ ′ ′
∂y ∕∂θ ∂y ∕∂a ∂y ∕∂b](source260x.png)
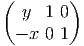 . Grâce à l’utilisation de
quelques abus de notations évidents, nous voyons que
. Grâce à l’utilisation de
quelques abus de notations évidents, nous voyons que
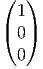 est
est
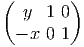
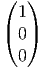 =
= 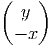 et donc
et donc 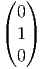 est
est
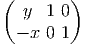
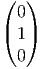 =
= 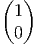 et donc
et donc  est
est
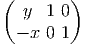
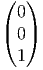 =
= 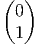 et donc
et donc 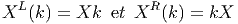
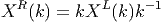
![L R
[X ,Y ] = 0](source276x.png)
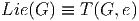
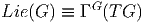
![[XR, Y R] = [X,Y ]R](source279x.png)
![[XL, Y L] = - [X, Y ]L](source280x.png)
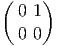 ,
,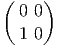 ,
,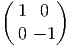
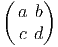 =
= 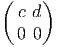
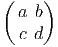
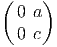
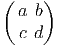 =
= 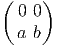
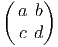
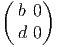
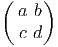 =
= 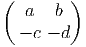
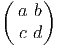
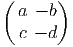
![[X3, X+-] = +2X+,- [XR3 ,XR+] = +2XR+, [XL3,XL+ ] = - 2XR+](source296x.png)
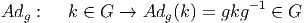
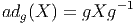
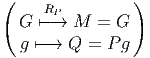
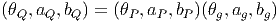
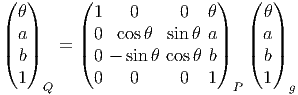
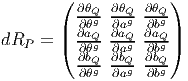
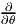 ,
, 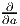 ,
,
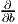 .
.
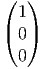 =
= 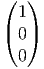 ,
, 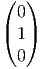 =
= 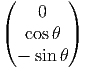 ,
,  =
= 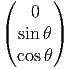 .
.
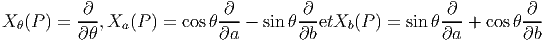
![[X θ,Xa ] = - Xb, [Xθ,Xb ] = +Xa et [Xa, Xb ] = 0](source313x.png)
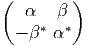 , obéissant à la condition
, obéissant à la condition
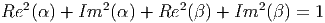
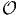
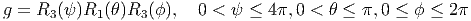
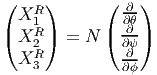
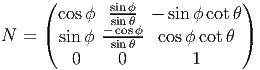
![[XR1 ,XR2 ] = - XR3 etc](source319x.png)
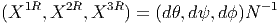
![[XL1 ,XL2 ] = +XL3 etc](source321x.png)
![R L
[X i ,Xj ] = 0](source322x.png)
 = fαγβ(P )X γ(P)](source323x.png)
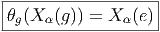
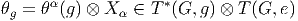
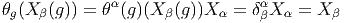
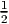
![[ω ∧ σ ] = [ωαX α ∧ σβX β ] = ω α ∧ ω β[X α,X β] = ω α ∧ σ βfγαβX γ](source328x.png)
![|-----------------|
|dθ + 12[θ ∧ θ] = 0 |
------------------](source329x.png)
 = [ω (u),σ(v)]](source330x.png)
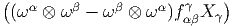 (
(![dθ + [θ,θ] = 0](source332x.png)
![1
dω - --[ω ∧ ω ] = 0
2](source333x.png)