1.2 Variétés différentiables
1.2.1 Variétés, cartes, atlas
Intuitivement, on peut considérer une variété différentiable comme une variété
topologique (voir exemples supra) qui soit “lisse”, c’est à dire sans plis, sans coins
etc. Une variété différentiable M de dimension n est donc avant tout une variété
topologique. Nous définissons tout s’abord la notion de carte qui généralise la
notion usuelle de carte géographique. Une carte consiste en la donnée d’un ouvert
Ui de M ainsi que d’une application x :  ∈ Ui ⊂ M
∈ Ui ⊂ M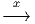 (xμ(
(xμ( )) ∈ I Rn avec
μ ∈{1…n}. Il importe de bien établir une distinction entre le point
)) ∈ I Rn avec
μ ∈{1…n}. Il importe de bien établir une distinction entre le point  lui-même et ce qu’on appelle ses coordonnées xμ(
lui-même et ce qu’on appelle ses coordonnées xμ( ) dans la carte choisie. On
suppose, de plus, que l’application x est bijective et bi-continue de Ui sur son
image.
) dans la carte choisie. On
suppose, de plus, que l’application x est bijective et bi-continue de Ui sur son
image.
Mis à part le cas relativement trivial où M est homéomorphe à I Rn, il
nous faut plusieurs cartes pour recouvrir la variété M. On appellera atlas
(sous-entendu différentiable) la donnée d’un ensemble de cartes (Ui,x) qui
recouvrent M c’est à dire telles que ∪iUi = M et telles que les changements de
cartes ϕij soient des bijections différentiables, ainsi que leurs inverses. Précisons ce
dernier point. Supposons que  ∈ Ui ∩ Uj ⊂ M, on peut donc représenter
∈ Ui ∩ Uj ⊂ M, on peut donc représenter  par un point xμ(
par un point xμ( ) de I Rn dans la carte (U
i,x) ou par un autre point
yμ(
) de I Rn dans la carte (U
i,x) ou par un autre point
yμ( ) de I Rn dans la carte (U
j,y). On note ϕij le changement de cartes
(encore appelé transformation de coordonnées) ; c’est une application de
l’ouvert x(Ui) de I Rn dans l’ouvert y(U
j) de I Rn. On sait ce que signifie
“différentiable” pour une application de I Rn dans I Rn : les dérivées partielles, par
rapport à chacune des variables, doivent exister. On impose donc à ϕij
d’être une application différentiable. On lui impose également d’être
bijective (donc inversible) et on impose à son inverse ϕji = ϕij-1 d’être
également différentiable. Bien entendu, il faut préciser un peu plus ce qu’on
entend par différentiable : suivant qu’on impose aux applications ϕij
d’être une seule fois différentiable, r fois différentiables ou infiniment
différentiables, on parle d’atlas de classe C1, Cr ou C∞. Dans la suite de
l’ouvrage et sauf mention explicite du contraire, c’est de classe C∞ qu’il
s’agira. La première façon de définir une variété différentiable est de se
donner une variété topologique ainsi qu’un atlas différentiable. Du pont de
vue des notations, il n’est pas très commode de faire figurer l’indice i
qui se rapporte à la carte, sur le système de coordonnées x ; dans le
cas où on en considère deux (par exemple x et y) on écrira les formules
de changement de carte (l’application ϕij) sans introduire de nouvelle
notation en écrivant simplement yμ comme une fonction de xν, c’est à dire
yμ = yμ(xν).
) de I Rn dans la carte (U
j,y). On note ϕij le changement de cartes
(encore appelé transformation de coordonnées) ; c’est une application de
l’ouvert x(Ui) de I Rn dans l’ouvert y(U
j) de I Rn. On sait ce que signifie
“différentiable” pour une application de I Rn dans I Rn : les dérivées partielles, par
rapport à chacune des variables, doivent exister. On impose donc à ϕij
d’être une application différentiable. On lui impose également d’être
bijective (donc inversible) et on impose à son inverse ϕji = ϕij-1 d’être
également différentiable. Bien entendu, il faut préciser un peu plus ce qu’on
entend par différentiable : suivant qu’on impose aux applications ϕij
d’être une seule fois différentiable, r fois différentiables ou infiniment
différentiables, on parle d’atlas de classe C1, Cr ou C∞. Dans la suite de
l’ouvrage et sauf mention explicite du contraire, c’est de classe C∞ qu’il
s’agira. La première façon de définir une variété différentiable est de se
donner une variété topologique ainsi qu’un atlas différentiable. Du pont de
vue des notations, il n’est pas très commode de faire figurer l’indice i
qui se rapporte à la carte, sur le système de coordonnées x ; dans le
cas où on en considère deux (par exemple x et y) on écrira les formules
de changement de carte (l’application ϕij) sans introduire de nouvelle
notation en écrivant simplement yμ comme une fonction de xν, c’est à dire
yμ = yμ(xν).
1.2.2 Atlas maximal
En géographie ordinaire (celle du globe terrestre) il est bien connu qu’il nous
faut au moins deux cartes pour décrire la Terre. Par contre, rien ne nous
interdit d’en utiliser trois ou plus …. Si on réunit les cartes d’un atlas avec
celles d’un atlas différent (concernant la même variété topologique), on
peut s’attendre à fabriquer ainsi un atlas plus grand, un peu redondant,
certes, mais néanmoins utile. Il faut cependant prendre la précaution
d’imposer aux cartes d’être compatibles, c’est à dire telles que les formules de
changements de cartes, d’un atlas à l’autre, puissent s’exprimer en terme de
transformations différentiables de I Rn. Cette précaution n’est pas inutile et
peut conduire à des surprises. Rien ne nous empêche alors de considérer
l’ensemble (assez gros il est vrai !) de tous les atlas compatibles possibles
d’une variété donnée et de les réunir en un unique atlas maximal. Bien
qu’un seul atlas suffise à caractériser complètement la variété, il peut
être très utile de considérer la variété M équipée d’un tel atlas maximal
contenant toutes les cartes compatibles possibles. En d’autres termes, on
peut complètement caractériser une variété différentiable par la donnée
d’une variété topologique et d’un atlas maximal. Il se trouve que, dans
certains cas, une variété topologique donnée possède plusieurs structures
différentiables (plusieurs atlas maximaux distincts). C’est le cas pour
IR4 (le seul, parmi les espaces numériques I Rn à posséder des structures
différentiables “exotiques”) et c’est aussi le cas pour les sphères Sn lorsque n ≥ 7.
Nous ne nous intéresserons pas à ces phénomènes dans le cadre de cet
ouvrage.
1.2.3 Variétés et calcul différentiel “intrinsèque”
En mathématiques élémentaires, on définit souvent les espaces géométriques
intéressants (par exemple une sphère) comme sous espace d’un espace affine
IRn. L’idée fondamentale du calcul sur les variétés (calcul différentiel
intrinsèque comme on l’appelait autrefois) est de faire abstraction du fait que la
variété qui nous intéresse est, ou non, plongée dans un espace I Rn “plus
grand” et de développer un calcul qui soit totalement indépendant du
plongement en question. Les motivations physiques sont analogues. Par exemple,
l’expérience quotidienne nous montre que tout événement de l’univers
sensible (whatever it means) peut se décrire à l’aide de quatre nombres
spécifiant sa position (trois nombres) et sa date (un nombre). Mais pourquoi
supposer, a priori que l’ensemble de ces événements doive être décrit à
l’aide d’un un espace I R4 ? Pourquoi pas une hyper-sphère (ou n’importe
quoi d’autre ?) Mais alors, si on décide d’utiliser une hyper-sphère de
dimension 4 pour décrire notre espace-temps, ou, comme dans certains
modèles cosmologiques, comme le produit d’une hyper-sphère (gonflable)
de dimension 3 par une droite ou une demi-droite, pourquoi supposer
que notre variété est plongée dans un espace de dimension 5 ou plus
dont les points sont sans signification physique ? Puisque c’est possible,
autant travailler dans la variété qui nous intéresse sans chercher à en
“sortir”.
L’idée la plus fondamentale et la plus simple du calcul différentiel sur les
variétés est la suivante. Grâce à l’existence locale des cartes, on peut
toujours faire “comme si” on était sur I Rn et développer des outils et des
méthodes de calcul sans se soucier – dans un premier temps – de leur
globalisation, quitte à vérifier, par la suite, que tout se recolle comme
il faut lorsqu’on passe d’une carte à l’autre. C’est ainsi que l’essentiel
des notions qui suivent sont en fait des notions qui peuvent être définies
dans un espace I Rn et dont la généralisation, au cas des variétés, est
quasi-immédiate. Nous ne supposons pas que le lecteur est déjà familier des
notions en question ; c’est la raison d’être des paragraphes qui suivent.
 ∈ Ui ⊂ M
∈ Ui ⊂ M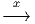 (xμ(
(xμ( )) ∈ I Rn avec
μ ∈{1…n}. Il importe de bien établir une distinction entre le point
)) ∈ I Rn avec
μ ∈{1…n}. Il importe de bien établir une distinction entre le point  lui-même et ce qu’on appelle ses coordonnées xμ(
lui-même et ce qu’on appelle ses coordonnées xμ( ) dans la carte choisie. On
suppose, de plus, que l’application x est bijective et bi-continue de Ui sur son
image.
) dans la carte choisie. On
suppose, de plus, que l’application x est bijective et bi-continue de Ui sur son
image.