3.4 Changement de groupe structural dans les fibrés principaux : élargissement et réduction

3.4.1 Définitions

On considère la situation où nous avons deux fibrés principaux Q(M,H) et P(M,G) avec H ⊂ G et f, un difféomorphisme de Q sur f(Q) ⊂ P tel que ∀z ∈ Q,∀s ∈ H,f(zs) = f(z)s. En pratique il s’agira souvent d’une inclusion Q ⊂ P, f n’étant autre que l’identité.

Dans une telle situation, on dit que P est un élargissement (ou un prolongement) de Q et que Q est une réduction de P.

Comme nous allons le voir, il est toujours possible d’élargir mais il n’est pas nécessairement possible de réduire.

3.4.2 Elargissement (passage de H à G avec H ⊂ G)

Soit Q = Q(M,H) un fibré principal. On veut “agrandir” le fibré Q sans modifier la base M mais en agrandissant la fibre, c’est à dire en remplaçant le groupe de Lie H par un groupe G “plus grand”. La construction est la suivante : on se choisit un groupe de Lie G tel que H ⊂ G et on construit le fibré P associé à Q défini par P = Q ×_HG où H agit sur G par multiplication à gauche. Les actions de H à droite de Q et à gauche de G s’annihilent, mais il est évident que l’espace P = P(M,G) est un G-fibré principal puisque G agit à droite de P via (z.k)k′ = z.kk′, avec z ∈ Q et k,k′∈ G. Par ailleurs, le difféomorphisme de Q sur f(Q) recherché est défini, pour z ∈ Q, par f(z) = z.e (e désignant l’élément neutre de G) et on notera simplement f(z) = z.

En conclusion, le passage de Q(M,H) à P(M,G) avec H ⊂ G est toujours possible. On dit que P est obtenu à partir de Q par élargissement du groupe structural et que Q lui-même est une réduction de P. Notons que les représentations de G sont toujours des représentations de H, mais que le contraire n’est pas nécessairement vrai (ainsi, il faut, en général, prendre la somme directe de plusieurs représentations de H pour construire une représentation de G) ; les fibrés associés à Q ne sont donc pas forcément toujours des fibrés associés à un élargissement P.

3.4.3 Réduction (passage de G à H avec H ⊂ G)

Méthode

Soit P = P(M,G) un fibré principal. On veut diminuer la taille de P sans modifier la base M mais en “raccourcissant” la fibre, c’est à dire en remplaçant G par un groupe “plus petit”. En d’autres termes, si on considère les éléments de P comme des repères généralisés, on veut s’intéresser uniquement à une sous-classe particulière de repères, sous-classe qui soit stable sous l’action d’un sous-groupe H de G. La méthode du paragraphe précédent ne s’applique pas car le groupe H(⊂ G) n’est pas stable lorsqu’on le multiplie à gauche par des éléments de G.

Enonçons (et retenons) le résultat suivant que nous démontrerons un peu plus bas :

Le choix d’une réduction du fibré principal P = P(M,G) à un sous-fibré Q = Q(M,H) de groupe structural H, lorsqu’il existe, n’est pas en général unique, et est caractérisé par le choix d’une section globale dans un fibré en espaces homogènes associé à P, en l’occurrence le fibré associé P ×_GG∕H.

Ce théorème est d’une importance fondamentale car il permet, comme nous allons le voir, de donner un sens précis à l’idée intuitive de “choix d’une géométrie” pour la variété différentiable M.

Preuve. Soit σ une section globale de E = PmodH. Un théorème précédemment discuté (voir les diverses manières de considérer les sections de fibré associé) nous dit qu’on peut associer à σ une application 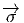du fibré principal P dans la fibre type G∕H, qui soit équivariante (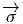(ys) = s^-1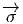(y)). Définissons Q = 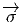^-1(eH) ⊂ P. La projection π : QM n’est autre, par définition, que la restriction à Q de la projection π de P. Considérons deux points y₁ et y₂ de la même fibre de Q, c’est à dire π(y₁) = π(y₂) ; nous savons qu’il existe s ∈ Gtel quey₂ = y₁s. Nous allons montrer qu’en fait, cet élément s appartient au sous-groupe H. En effet,

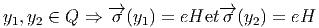
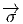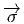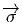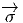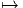mais (y₂) = (y₁s) = s^-1(y ₁) et donc, eH = s^-1(eH), ce qui montre que s ∈ H. Ainsi Q ⊂ P est un fibré principal de groupe structural H. Réciproquement, donnons nous H ⊂ G et une réduction Q = Q(M,H) ⊂ P = P(M,G). Définissons : PG∕H par ∀y ∈ Q ⊂ P,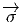(y) = eH ∈ G∕H. La fonction 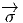est ainsi constante sur les fibres de Q. Soient maintenant deux points y₀ ∈ Q et y ∈ P que nous prenons dans la même fibre de P mais nous supposons que y n’appartient pas nécessairement à Q. Il existe donc un élément g de G tel que y = y₀g, alors 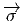(y) = 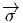(y₀g) = g^-1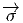(y ₀) = g^-1eH = g^-1H ∈ G∕H. 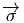On a ainsi construit une application : PG∕H équivariante sous l’action de G. Cela détermine, en vertu du théorème énoncé au 2 du 3.3.10 une section globale de E(M,G∕H) = PmodH.

Réduction de GL(n, I R) à SO(n) : structures riemanniennes

 
On peut rattacher canoniquement à une variété différentiable M son fibré FM des repères linéaires. C’est un fibré principal de groupe structural GL(n, I R). Choisissons maintenant une réduction à un sous-fibré de groupe structural SO(n). Choisir une telle réduction consiste à sélectionner une certaine classe de repères, que nous appellerons orthonormés, telle que l’un quelconque d’entre eux puisse s’obtenir à partir de n’importe quel autre à l’aide d’une matrice du groupe orthogonal SO(n). Par définition, une variété riemannienne (M en l’occurrence) est une variété différentiable de dimension n pour laquelle on a choisi une réduction du fibré FM des repères linéaires à un sous-fibré de groupe structural SO(n). Le sous-fibré en question se note alors OFM (“Orthogonal Frame Bundle”) et prend le nom de fibré des repères orthonormés. Le lecteur peut se demander où est la métrique dans cette approche… La réponse est la suivante : le tenseur métrique s’identifie précisément avec la section globale du fibré en espaces homogènes GL(n)∕SO(n) qui définit la réduction (nous oublions momentanément les problèmes liés à des exigences de non dégénérescence, de positivité etc ). Noter que la dimension de cet espace homogène est égale à dim(GL(n)) - dim(SO(n)) = n² - n(n - 1)∕2 = n(n + 1)∕2, et ses éléments peuvent donc s’identifier, comme il se doit, à des tenseurs de rang deux complètement symétriques. Intuitivement, choisir une structure riemannienne revient à conférer une “forme géométrique” à une variété différentiable ; c’est ainsi que c’est le choix de la métrique qui fait la différence entre un ballon de foot, un ballon de rugby et… une bouteille de vin (bouchée !) et la multiplicité des réductions possibles coïncide avec la multiplicité des métriques riemanniennes qu’on peut choisir, pour une variété différentiable donnée. Vu l’importance de cette notion, nous y reviendrons abondamment dans le chapitre suivant.

Réduction de GL(2n, I R) à GL(n,lC) : structures presque-complexes

L’idée est essentiellement la même que dans l’exemple précédent, à ceci près que M est supposé être de dimension paire et qu’on choisit maintenant une réduction du fibré des repères linéaires à un sous-fibré dont le groupe orthogonal doit être SU(n). Les variétés pour lesquelles on a effectué un tel choix se nomment variétés presque-complexes et l’analogue de la métrique est ici la donnée, en chaque espace tangent T(M,x) d’un endomorphisme j de carré égal à -1. Cet opérateur peut encore s’identifier à une section globale d’un fibré en espaces homogènes GL(2n, I R)∕GL(n, lC). Le lecteur peut sans doute se demander pourquoi on parle ici de variétés presque-complexes et non, tout simplement, de variétés complexes. Il se trouve que ces deux notions sont de nature assez différentes (et la terminologie est désormais consacrée) : la notion de structure presque-complexe est, comme on vient de le voir, analogue à la notion de structure riemannienne et est associée au choix d’une réduction du fibré des repères pour une variété différentiable ; la notion de structure complexe est, quant à elle, analogue à la notion de structure de variété topologique, de variété linéaire par morceaux ou analogue à la notion de structure différentiable elle-même (on choisit des cartes à valeur dans lCⁿ et non plus dans I Rⁿ et on impose aux fonctions de transitions d’être holomorphes). Nous n’aurons pas le loisir, dans cet ouvrage, d’étudier la géométrie des variétés complexes ; notons simplement que la terminologie vient du fait qu’une variété complexe donnée fournit une variété différentiable qui se trouve automatiquement munie d’une structure presque-complexe (l’endomorphisme j de carré égal à -1 provenant tout simplement de la multiplication par le nombre complexe i). Le passage inverse, celui d’une structure presque-complexe à une structure complexe, n’est pas automatique car il nécessite la vérification d’une certaine condition d’intégrabilité.

On peut aussi parler de variétés presque-hermitiennes lorsque la réduction du groupe structural va de GL(2n, I R) à U(n) = O(2n) ∩ GL(n, lC). Dans ce cas, il existe une métrique h compatible avec la structure presque-complexe, en ce sens que h(v₁,v₂) = h(jv₁,jv₂). On peut alors construire une forme hermitienne H(v₁,v₂) = 1 2(h(v₁,v₂)- ih(jv₁,v₂)) et une forme presque-Kählerienne ω(v₁,v₂) = h(jv₁,v₂).

Réduction de GL(4,n) à Sp(n) : structures presque-quaternioniques

L’histoire est la même que dans le cas précédent et les commentaires sont analogues. La section globale du fibré en espaces homogènes GL(4n, I R)∕Sp(n) caractérisant la réduction peut s’identifier à la donnée, en chaque espace tangent T(M,x) de trois opérateurs j₁, j₂, j₃, tous trois de carré égal à moins l’identité, et satisfaisant aux relations j₁j₂ = -j₂j₁ = j₃, j₂j₃ = -j₃j₂ = j₁ et j₃j₁ = -j₁j₃ = j₂. La raison du “presque” dans le presque-quaternionique est analogue celle donnée dans le paragraphe précédent à condition toutefois de remplacer nombres complexes par quaternions. Ici Sp(n) désigne le groupe compact des unitaires quaternioniques, quelquefois désigné par U(n, I H). Nous n’aurons pas le loisir de revenir sur ce sujet dans le cadre de cet ouvrage.

Remarques

Avant de quitter cette partie consacrée aux réductions de fibrés principaux, notons que les représentations d’un groupe G sont aussi des représentations de tout sous-groupe H de G. Ainsi donc, les fibrés associés à P(M,G) sont aussi associés à tout sous-fibré Q(M,H) avec H ⊂ G. Il est rassurant de savoir que le fibré tangent TM défini à partir du fibré des repères linéaires FM coïncide avec celui qu’on peut définir à partir du fibré OFM des repères orthonormés !