 avec G ~
avec G ~ |H)
|H)Les deux sous-sections précédentes étaient, en quelque sorte, complémentaires, les deux qui suivent le seront aussi.
 avec G ~
avec G ~ |H)
|H)Le problème est le suivant : on part d’un espace fibré P = P(M,G)
et on veut remplacer le groupe structural G par un groupe  tel
que G soit isomorphe à
tel
que G soit isomorphe à  ∕H où H est un sous-groupe distingué de
∕H où H est un sous-groupe distingué de
 . Le cas le plus fréquent est celui où G est un groupe qui n’est
pas simplement connexe et où on veut le remplacer par son groupe
de recouvrement universel
. Le cas le plus fréquent est celui où G est un groupe qui n’est
pas simplement connexe et où on veut le remplacer par son groupe
de recouvrement universel  . H est alors un sous-groupe discret du
centre de
. H est alors un sous-groupe discret du
centre de  et s’identifie au groupe d’homotopie π1(G) (voir le chapitre
sur les groupes). Pour illustrer cette situation, voici un exemple
dont l’importance physique est importante. La variété différentiable
M est un modèle pour l’espace-temps et P désigne le fibré des
repères orthonormés correspondant au choix d’une certaine métrique
sur M. Certains champs de matière vont être représentés par des
sections de fibrés associés à P. Ces fibrés seront construits à partir de
représentations du groupe SO(n) (en physique quadri-dimensionelle,
généralement SO(3, 1) ou SO(4)). Dans bien des cas, cependant, les
champs de matière qui nous intéressent ne correspondent pas vraiment
à des représentations de SO(n) mais à des représentations de son
groupe de recouvrement universel Spin(n) c’est à dire Spin(3, 1) =
SL(2, lC) si G = SO(3, 1) et Spin(4) = SU(2) × SU(2) si G = SO(4).
On se souvient en effet que les représentations de G peuvent également
être considérées comme des représentations de
et s’identifie au groupe d’homotopie π1(G) (voir le chapitre
sur les groupes). Pour illustrer cette situation, voici un exemple
dont l’importance physique est importante. La variété différentiable
M est un modèle pour l’espace-temps et P désigne le fibré des
repères orthonormés correspondant au choix d’une certaine métrique
sur M. Certains champs de matière vont être représentés par des
sections de fibrés associés à P. Ces fibrés seront construits à partir de
représentations du groupe SO(n) (en physique quadri-dimensionelle,
généralement SO(3, 1) ou SO(4)). Dans bien des cas, cependant, les
champs de matière qui nous intéressent ne correspondent pas vraiment
à des représentations de SO(n) mais à des représentations de son
groupe de recouvrement universel Spin(n) c’est à dire Spin(3, 1) =
SL(2, lC) si G = SO(3, 1) et Spin(4) = SU(2) × SU(2) si G = SO(4).
On se souvient en effet que les représentations de G peuvent également
être considérées comme des représentations de 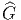 mais que certaines
représentations de
mais que certaines
représentations de  ne correspondent à aucune représentation de G
(ainsi, les spins demi-entiers correspondent à des représentations de
SU(2) mais pas à des représentations de SO(3)). Lorsque la topologie
de M et triviale, le fait de “considérer des spineurs” n’offre aucune
difficulté ; les choses changent lorsque M cesse d’être trivial : en
d’autre termes, il existe des espaces qui n’admettent pas de spineurs !
A l’opposé, il existe des espaces qui admettent plusieurs types de
spineurs. Nous discuterons de nouveau de ces problèmes un peu plus
loin.
ne correspondent à aucune représentation de G
(ainsi, les spins demi-entiers correspondent à des représentations de
SU(2) mais pas à des représentations de SO(3)). Lorsque la topologie
de M et triviale, le fait de “considérer des spineurs” n’offre aucune
difficulté ; les choses changent lorsque M cesse d’être trivial : en
d’autre termes, il existe des espaces qui n’admettent pas de spineurs !
A l’opposé, il existe des espaces qui admettent plusieurs types de
spineurs. Nous discuterons de nouveau de ces problèmes un peu plus
loin.
Revenons à un cadre plus général. On se donne G = Ĝ∕H. On a donc
un homomorphisme (surjectif) de groupe 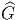
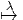 G de noyau H = Kerλ.
On appellera “extension de fibré principal P = P(M,G) à un fibré
de groupe structural
G de noyau H = Kerλ.
On appellera “extension de fibré principal P = P(M,G) à un fibré
de groupe structural 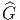 ” la donnée d’un fibré principal
” la donnée d’un fibré principal 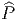 =
= 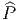 (M,
(M,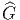 )
et d’un homomorphisme de fibré
)
et d’un homomorphisme de fibré 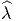 :
: 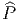
 P qui soit compatible
avec les actions respectives de G et
P qui soit compatible
avec les actions respectives de G et 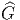 et avec l’homomorphisme de
groupe λ ; en d’autres termes,
et avec l’homomorphisme de
groupe λ ; en d’autres termes, 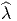 doit préserver les fibres (c’est un
homomorphisme de fibré) et être tel que
doit préserver les fibres (c’est un
homomorphisme de fibré) et être tel que
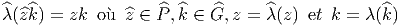
Le problème de l’extension d’un fibré principal (passage de G à 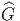 avec
G =
avec
G = 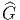 ∕H) peut être décrit de façon imagée par la figure suivante
(3.18).
∕H) peut être décrit de façon imagée par la figure suivante
(3.18).
On voit que 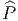 est aussi un H-fibré principal au dessus de P (voir
également la discussion menée en section 3.3.4) et que P ~
est aussi un H-fibré principal au dessus de P (voir
également la discussion menée en section 3.3.4) et que P ~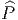 ∕H.
∕H.
Dans le cas particulier où P = OFM désigne le fibré des repères
orthonormés d’une variété riemannienne M, le groupe structural est
G = SO(n) et 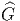 = Spin(n). On dit que la variété M est une variété
spinorielle s’il existe une extension
= Spin(n). On dit que la variété M est une variété
spinorielle s’il existe une extension 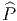 =
= 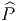 (M,Spin(n)). Choisir une
structure spinorielle pour une variété riemannienne donnée M consiste à
choisir une extension
(M,Spin(n)). Choisir une
structure spinorielle pour une variété riemannienne donnée M consiste à
choisir une extension 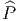 (s’il en existe une). Le fibré
(s’il en existe une). Le fibré 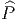 , s’il existe,
est alors désigné sous le nom de fibré des repères spinoriels ou,
tout simplement fibré de spin et dénoté
, s’il existe,
est alors désigné sous le nom de fibré des repères spinoriels ou,
tout simplement fibré de spin et dénoté  FM. Dans les bons cas
(“bon” signifiant qu’on peut ne pas se soucier du problème !),
FM. Dans les bons cas
(“bon” signifiant qu’on peut ne pas se soucier du problème !),
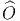 FM existe et est unique, à isomorphisme près. Notons encore que
le choix d’une structure spinorielle est tributaire du choix d’une
structure riemannienne (on choisit d’abord P = P(M,SO(n)), puis
FM existe et est unique, à isomorphisme près. Notons encore que
le choix d’une structure spinorielle est tributaire du choix d’une
structure riemannienne (on choisit d’abord P = P(M,SO(n)), puis
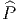 =
= 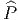 (M,Spin(n)), mais on doit se souvenir que deux métriques
distinctes définissent des fibrés P(M,SO(n)) différents. On sait que la
représentation fondamentale de SO(n) agissant sur I Rn permet de
fabriquer le fibré tangent TM = P ×SO(n)I Rn comme fibré associé à
P et de définir l’ensemble des champs de vecteurs ΓTM comme
ensemble des sections de TM. De la même façon, la représentation
fondamentale de Spin(n) agissant sur lCs avec s = 2[n∕2], [n∕2] désignant la
partie entière de n∕2, permet de fabriquer le fibré des spineurs
SM =
(M,Spin(n)), mais on doit se souvenir que deux métriques
distinctes définissent des fibrés P(M,SO(n)) différents. On sait que la
représentation fondamentale de SO(n) agissant sur I Rn permet de
fabriquer le fibré tangent TM = P ×SO(n)I Rn comme fibré associé à
P et de définir l’ensemble des champs de vecteurs ΓTM comme
ensemble des sections de TM. De la même façon, la représentation
fondamentale de Spin(n) agissant sur lCs avec s = 2[n∕2], [n∕2] désignant la
partie entière de n∕2, permet de fabriquer le fibré des spineurs
SM = 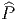 ×Spin(n)lCs comme fibré associé à
×Spin(n)lCs comme fibré associé à 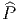 et de définir l’ensemble
des champs de spineurs ΓSM comme ensemble des sections de
SM.
et de définir l’ensemble
des champs de spineurs ΓSM comme ensemble des sections de
SM.
Pour ce qui est des rappels concernant la représentation fondamentale de Spin(n), les algèbres de Clifford, etc , voir la fin du chapitre précédent.
On montre que l’existence d’une structure spinorielle, pour une variété donnée, est liée à l’annulation d’une certaine classe caractéristique (la deuxième classe de Stiefel-Whitney). Mis à part une courte remarque du même type à la fin de cette section, ce phénomène ne sera pas discuté dans le cadre de notre ouvrage.
En physique théorique, on montre que, dans le cadre de la théorie quantique des champs, et en dimension égale à 4, les particules obéissant à une statistique de Fermi-Dirac (les fermions) sont des particules de spin demi-entier, alors que celles obéissant à une statistique de Bose-Einstein (les bosons) sont des particules de spin entier. Nous n’expliquerons pas ici la signification de ce résultat célèbre (le théorème spin-statistique) puisque nous n’aborderons pas la théorie quantique des champs dans le cadre de cet ouvrage. Cependant, le résultat en question (qui n’est vraiment bien compris et démontré qu’en dimension 4) nous permet d’introduire la terminologie suivante en dimension quelconque : nous dirons qu’un champ est un champ bosonique s’il s’agit d’une section d’un fibré vectoriel associable au fibré des repères orthonormés d’une variété riemannienne M ; nous dirons que c’est un champ fermionique s’il s’agit d’une section d’un fibré vectoriel associable au fibré des repères spinoriels d’une variété riemannienne M, qui soit telle que la représentation correspondante (celle qui définit le fibré associé) soit une représentation de Spin(n) qui ne puisse pas être considérée comme une représentation du groupe SO(n) mais seulement comme une représentation de Spin(n).
Notons que, bien que moins proche de notre intuition, les champs spinoriels (sections de SM) sont plus “fondamentaux” que les champs vectoriels (sections de TM). Ceci est déjà évident au niveau de la théorie des représentations de SU(2) : on peut construire n’importe quelle représentation de ce groupe à partir de la fondamentale (qui est spinorielle ). Cette dernière est de dimension 2 et correspond physiquement à ce qu’on appelle un champ de spin 1∕2. Par ailleurs, il est facile de voir qu’on peut construire un champ de vecteurs à partir de (deux) champs de spineurs, mais pas le contraire…
Nous venons de discuter le cas particulier de G = SO(n) = Spin(n)∕Z Z2 mais nous aurions pu également considérer le cas de fibrés avec groupe structural G = SU(3)∕Z Z3 : le fait qu’il soit, ou non, possible, de définir des “champs de quarks” (associés à la représentation fondamentale de SU(3), ou plus généralement des champs associés à des représentations dont la trialité est différente de zéro) pour une variété M considérée comme base d’un fibré principal P(M,SU(3)∕Z Z3) n’est pas quelque chose d’automatique…. On pourrait alors parler de “structure quarkique” !
Il ne faudrait pas croire que le groupe H, tel que G = 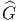 ∕H dont il a
été question dans ce chapitre consacré aux extensions d’espaces
fibrés soit nécessairement discret. C’est ainsi qu’en théorie des
cordes, la variété M est remplacée par LM (le “loopspace” de M),
c’est à dire l’ensemble des applications de S1 dans M, G est, de la
même façon remplacé par LG et P par LP. L’ensemble LG est
naturellement un groupe (de dimension infinie) et LP est fibré en
LG au dessus de LM. Dans ce cas, toutefois, ce ne sont pas tant
les représentations de LG qui nous intéressent, mais celles d’une
extension centrale
∕H dont il a
été question dans ce chapitre consacré aux extensions d’espaces
fibrés soit nécessairement discret. C’est ainsi qu’en théorie des
cordes, la variété M est remplacée par LM (le “loopspace” de M),
c’est à dire l’ensemble des applications de S1 dans M, G est, de la
même façon remplacé par LG et P par LP. L’ensemble LG est
naturellement un groupe (de dimension infinie) et LP est fibré en
LG au dessus de LM. Dans ce cas, toutefois, ce ne sont pas tant
les représentations de LG qui nous intéressent, mais celles d’une
extension centrale 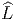 G de LG (on a Lie(
G de LG (on a Lie(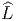 G) = Lie(LG) ⊕ I R).
Dans ce cas, H = U(1) et la question se pose de savoir si LP peut
être étendu à un fibré
G) = Lie(LG) ⊕ I R).
Dans ce cas, H = U(1) et la question se pose de savoir si LP peut
être étendu à un fibré 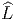 P de groupe structural
P de groupe structural 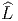 G. Là encore,
l’existence n’est pas assurée, et, en cas d’existence, l’unicité non
plus. Lorsque
G. Là encore,
l’existence n’est pas assurée, et, en cas d’existence, l’unicité non
plus. Lorsque 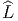 P existe, on dit que le fibré en boucles LP possède
une structure encordée (“a string structure for a loop bundle”
…).
P existe, on dit que le fibré en boucles LP possède
une structure encordée (“a string structure for a loop bundle”
…).
L’existence et l’unicité (ou non) des extensions de fibrés peuvent se décrire
de façon cohomologique. Cette interprétation dépasse le cadre que nous
nous sommes fixés. Mentionnons seulement que l’existence de 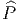 peut être
lié à l’annulation d’une certaine classe de cohomologie appartenant à
H2(M,H). Dans le cas des structures spinorielles, H = Z Z
2 et la classe en
question, dont l’annulation fournit une condition nécessaire et suffisante à
l’existence de
peut être
lié à l’annulation d’une certaine classe de cohomologie appartenant à
H2(M,H). Dans le cas des structures spinorielles, H = Z Z
2 et la classe en
question, dont l’annulation fournit une condition nécessaire et suffisante à
l’existence de 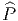 , s’appelle deuxième classe de Stiefel-Whitney . Dans
le cas des structures encordées, il faut considérer H2(LM,U(1))
puisque LM est la base du fibré considéré, ce groupe de cohomologie
(de LM) peut alors être relié à H3(M, Z Z) et … ceci est une autre
histoire.
, s’appelle deuxième classe de Stiefel-Whitney . Dans
le cas des structures encordées, il faut considérer H2(LM,U(1))
puisque LM est la base du fibré considéré, ce groupe de cohomologie
(de LM) peut alors être relié à H3(M, Z Z) et … ceci est une autre
histoire.
On part de P = P(M,G), on se choisit un sous-groupe distingué H de G et on veut remplacer P par Q = Q(M,K), avec K = G|H. Cette opération est, en un sens, inverse de celle précédemment considérée. La méthode est simple puisqu’il s’agit de “diviser” P par H en considérant l’ensemble quotient Q = P∕H où l’action de H sur P est obtenue par restriction de celle de G. Il est évident que ce type de changement de groupe structural n’offre aucune difficulté, contrairement à la situation inverse décrite au paragraphe précédent. Il faut évidemment veiller à ce que H soit distingué dans G, de façon à ce que le quotient G|H soit bien un groupe. Nous n’en dirons pas plus sur ce sujet puisque la discussion résulte simplement des analyses déjà effectuées dans les sections précédentes. En particulier, P est un H-fibré principal au dessus du fibré quotient Q, lequel se trouve être, également, dans ce cas particulier, un fibré principal.