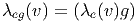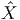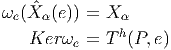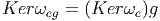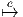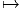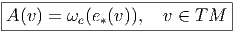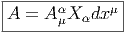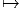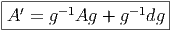4.1 Connexions dans un fibré principal
4.1.1 Motivations
On veut donner un sens à l’idée de vouloir “garder un repère fixe” ou de
“transporter son repère avec soi” ; il s’agit là d’une notion intuitive qui n’a, a
priori, pas de sens lorsqu’on se déplace sur une variété différentiable quelconque
munie de sa seule structure de variété. Intuitivement, on souhaite disposer d’un
moyen d’assujettir le déplacement d’un repère choisi (déplacement qui a donc lieu
dans l’ensemble des repères) lorsqu’on déplace l’origine de ce repère dans l’espace
qui nous intéresse. Puisque nous avons maintenant à notre disposition la notion
d’espace fibré, nous nous plaçons dans le fibré des repères correspondant à une
variété M (la base du fibré en question) et nous souhaitons donc pouvoir disposer
d’une méthode nous permettant d’associer, à tout chemin allant du point  au
point
au
point 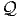 sur la base, et à tout repère au point
sur la base, et à tout repère au point  , un certain chemin dans
l’espace des repères. Choisir d’une telle méthode revient précisément à
choisir ce qu’on appelle une connexion dans le fibré principal des repères
linéaires. Le mot “connexion” – en anglais “connection”– est bien choisi
puisqu’il nous permet effectivement de connecter (de comparer) des vecteurs
(plus généralement des éléments d’un fibré associé) situés en des points
différents de la variété. Le cas de l’espace affine Rn est très particulier
puisqu’on peut disposer là de repères globaux permettant de comparer
des vecteurs situés en des points différents ; il existe d’autres variétés
pour lesquelles cette propriété est également valable et où le choix d’un
repère mobile global est possible : ce sont les variétés parallèlisables déjà
mentionnées dans le chapitre précédent. Nous allons, dans un premier
temps, définir la notion de connexion de façon infinitésimale, comme
étant un moyen d’associer un déplacement infinitésimal dans l’espace des
repères à un déplacement infinitésimal du point de base (c’est à dire du
point où le repère est situé). En fait, la seule structure utilisée dans la
définition de la notion de connexion est celle de fibré principal et tout ce
qu’on écrira aura encore un sens si on remplace le fibré des repères par un
fibré principal quelconque (cela dit, il est bien commode de visualiser les
choses en utilisant des repères, nous nous permettrons donc d’utiliser
le mot “repère” pour désigner un élément d’un espace fibré principal
quelconque).
, un certain chemin dans
l’espace des repères. Choisir d’une telle méthode revient précisément à
choisir ce qu’on appelle une connexion dans le fibré principal des repères
linéaires. Le mot “connexion” – en anglais “connection”– est bien choisi
puisqu’il nous permet effectivement de connecter (de comparer) des vecteurs
(plus généralement des éléments d’un fibré associé) situés en des points
différents de la variété. Le cas de l’espace affine Rn est très particulier
puisqu’on peut disposer là de repères globaux permettant de comparer
des vecteurs situés en des points différents ; il existe d’autres variétés
pour lesquelles cette propriété est également valable et où le choix d’un
repère mobile global est possible : ce sont les variétés parallèlisables déjà
mentionnées dans le chapitre précédent. Nous allons, dans un premier
temps, définir la notion de connexion de façon infinitésimale, comme
étant un moyen d’associer un déplacement infinitésimal dans l’espace des
repères à un déplacement infinitésimal du point de base (c’est à dire du
point où le repère est situé). En fait, la seule structure utilisée dans la
définition de la notion de connexion est celle de fibré principal et tout ce
qu’on écrira aura encore un sens si on remplace le fibré des repères par un
fibré principal quelconque (cela dit, il est bien commode de visualiser les
choses en utilisant des repères, nous nous permettrons donc d’utiliser
le mot “repère” pour désigner un élément d’un espace fibré principal
quelconque).
4.1.2 Distributions horizontales équivariantes
Soit P le fibré principal des repères linéaires de la variété M, avec groupe
structural GL(n). Soit e ∈ P un repère au point  ∈ M (attention e ne désigne
pas l’élément neutre de G !). L’espace tangent T(P,e), tangent à P en e est,
intuitivement, l’ensemble des déplacements infinitésimaux de repères, issus du
repère e. Nous savons déjà nous déplacer dans la direction verticale puisque cela
correspond à un déplacement infinitésimal induit par l’action du groupe GL(n) :
on fait “tourner” le repère e sans faire bouger le point
∈ M (attention e ne désigne
pas l’élément neutre de G !). L’espace tangent T(P,e), tangent à P en e est,
intuitivement, l’ensemble des déplacements infinitésimaux de repères, issus du
repère e. Nous savons déjà nous déplacer dans la direction verticale puisque cela
correspond à un déplacement infinitésimal induit par l’action du groupe GL(n) :
on fait “tourner” le repère e sans faire bouger le point  . Le sous espace vertical
V (P,e) est donc déjà bien défini. Une connexion sera caractérisée par le choix
d’un sous-espace supplémentaire à V (P,e) dans T(P,e), sous-espace qui sera
bien évidemment qualifié d’“horizontal” et noté H(P,e). Par ailleurs, on
veut que ce choix puisse être effectué, de façon continue et différentiable,
pour tout repère, c’est à dire en tout point e de P. Enfin, on veut que ce
choix soit également équivariant sous l’action du groupe structural : nous
savons que GL(n) opère transitivement sur les fibres (par exemple sur les
repères au point
. Le sous espace vertical
V (P,e) est donc déjà bien défini. Une connexion sera caractérisée par le choix
d’un sous-espace supplémentaire à V (P,e) dans T(P,e), sous-espace qui sera
bien évidemment qualifié d’“horizontal” et noté H(P,e). Par ailleurs, on
veut que ce choix puisse être effectué, de façon continue et différentiable,
pour tout repère, c’est à dire en tout point e de P. Enfin, on veut que ce
choix soit également équivariant sous l’action du groupe structural : nous
savons que GL(n) opère transitivement sur les fibres (par exemple sur les
repères au point  ), l’image du repère e sous l’action d’ un élément g du
groupe structural est un repère e.g de la même fibre (Rg(e) = e.g) et
l’application tangente dRg ≡ (Rg)* en e envoie donc l’espace tangent
T(P,e) dans l’espace tangent T(P,e.g). Il est commode de noter simplement
T(P,e)g = (Rg)*T(P,e) ⊂ T(P,eg) puisque, formellement ∂(ge)∕∂e = g. La
propriété d’équivariance requise signifie simplement ceci : on veut que le choix de
l’espace horizontal H(P,e.g) en e.g puisse également être obtenu en utilisant
l’action du groupe structural sur les fibres, en d’autres termes on impose
H(P,e.g) = H(P,e).g
), l’image du repère e sous l’action d’ un élément g du
groupe structural est un repère e.g de la même fibre (Rg(e) = e.g) et
l’application tangente dRg ≡ (Rg)* en e envoie donc l’espace tangent
T(P,e) dans l’espace tangent T(P,e.g). Il est commode de noter simplement
T(P,e)g = (Rg)*T(P,e) ⊂ T(P,eg) puisque, formellement ∂(ge)∕∂e = g. La
propriété d’équivariance requise signifie simplement ceci : on veut que le choix de
l’espace horizontal H(P,e.g) en e.g puisse également être obtenu en utilisant
l’action du groupe structural sur les fibres, en d’autres termes on impose
H(P,e.g) = H(P,e).g
Noter que la discussion qui précède ne dépend pas du type particulier de fibré
principal considéré et le lecteur est invité à remplacer partout le groupe GL(n)
par un groupe de Lie quelconque (et le mot “repère” par les mots “élément
du fibré principal P”). Le choix, en tout point e d’un fibré principal P,
d’un tel espace vectoriel H(P,e) supplémentaire à V (P,e), c’est à dire,
T(P,e) = V (P,e) ⊕H(P,e), est désigné sous le nom de distribution horizontale ;
noter que le sens de ce mot “distribution” n’a ici aucun rapport avec celui utilisé
en théorie de la mesure (la théorie des distributions !). Notre première définition
d’une connexion principale est donc la suivante : c ’est la donnée, dans un fibré
principal P, d’une distribution horizontale équivariante sous l’action du groupe
structural.
4.1.3 Relèvement horizontal
Soit P = P(M,G) un fibré principal, on dispose donc d’une projection π : P → M
et donc également de son application tangente π*. Cette application linéaire
envoie l’espace tangent T(P,e) sur l’espace tangent T(M,π(e)) ; en d’autres
termes, elle nous permet d’associer, à tout déplacement infinitésimal d’un repère
e dans l’espace des repères, le déplacement infinitésimal correspondant du point
x = π(e) dans la variété M (x est le point où le repère est centré). Comme nous
l’avons remarqué à plusieurs reprises, étant donnée une application d’une variété
dans une autre, nous pouvons faire “voyager” les vecteurs dans la même direction
–il s’agit d’un “push-forward”– et les formes dans la direction opposée
(“pull-back”)
De façon générale, soit γ(t) une courbe dans M, on dira qu’une courbe Γ(t)
dans P est un relèvement de γ(t) si Γ se projette sur γ (intuitivement “on” –un
voyageur qui se promène sur M– s’est choisi un repère mobile quelconque en tout
point du chemin qu’il suit). Supposons maintenant que nous nous sommes donnés
une connexion (au sens donné dans la sous section précédente) dans le
fibré principal P, nous savons donc définir l’horizontalité des vecteurs de
TP ; on dira qu’un relèvement est horizontal si les vecteurs tangents
au relèvement sont horizontaux. Considérons une courbe γ(t) dans M
allant de  0 = γ(0) à
0 = γ(0) à  1 = γ(1) et son relèvement horizontal issu de
e0 ∈ P, c’est à dire la courbe Γ(t) dans P. En utilisant les théorèmes
habituels concernant les équations différentielles, on montre qu’il y a
unicité du relèvement Γ de γ issus de e0. On dira que e1 = Γ(1) est le
transporté par parallélisme de e0 le long de γ par rapport à la connexion
choisie.
1 = γ(1) et son relèvement horizontal issu de
e0 ∈ P, c’est à dire la courbe Γ(t) dans P. En utilisant les théorèmes
habituels concernant les équations différentielles, on montre qu’il y a
unicité du relèvement Γ de γ issus de e0. On dira que e1 = Γ(1) est le
transporté par parallélisme de e0 le long de γ par rapport à la connexion
choisie.
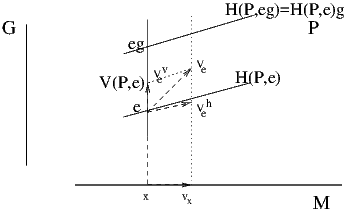
Nous définirons l’application de relèvement horizontal comme suit : soit x un
point de M et e un repère quelconque en x (c’est à dire un élément de la
fibre au dessus de x), soit vx un vecteur appartenant à l’espace tangent à
M en x, on désignera par λe(vx) l’élément de l’espace tangent T(P,e)
qui, d’une part, est horizontal et qui, d’autre part, se projette sur vx
grâce à l’application π*. Il est bien évident que ce vecteur est unique : Il
suffit de choisir un relevé quelconque de vx en e (c’est à dire un vecteur
quelconque V e de T(P,e) qui se projette sur vx, puis de le décomposer en une
partie verticale V ev et une partie horizontale V
eh = λ
e(vx) (c’est le vecteur
cherché) en utilisant la décomposition de T(P,e) en deux sous-espaces
supplémentaires.
La distribution horizontale n’étant pas quelconque (elle est équivariante !),
l’application de relèvement horizontal n’est pas quelconque non plus : le relevé du
vecteur v en eg doit coïncider avec l’image, par l’application tangente du
relevé de v en e. En clair, λeg(v) = (Rg)*(λe(v)), qu’on peut écrire plus
simplement
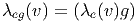 On
vient de décrire la façon dont on peut, grâce à la donnée d’une connexion, relever
les vecteurs tangents de M à P. Bien entendu, à condition de travailler
de façon duale, on peut faire quelque chose d’analogue avec les formes
différentielles. Plus précisément, le “pull-back” de la projection π est défini
sur les vecteurs cotangents à M et à valeurs dans le fibré cotangent de
P. La donnée d’une connexion (et donc de l’application de relèvement
horizontal) permet, à l’inverse, de projeter les formes de T*P sur les formes de
T*M.
On
vient de décrire la façon dont on peut, grâce à la donnée d’une connexion, relever
les vecteurs tangents de M à P. Bien entendu, à condition de travailler
de façon duale, on peut faire quelque chose d’analogue avec les formes
différentielles. Plus précisément, le “pull-back” de la projection π est défini
sur les vecteurs cotangents à M et à valeurs dans le fibré cotangent de
P. La donnée d’une connexion (et donc de l’application de relèvement
horizontal) permet, à l’inverse, de projeter les formes de T*P sur les formes de
T*M.
Toute cette discussion peut être résumée à l’aide de la figure ci-dessous.
4.1.4 Forme de connexion
Il existe plusieurs façons de définir la notion de connexion et nous venons d’en
mentionner deux (distribution horizontale équivariante et application de
relèvement horizontal) dont l’interprétation géométrique est intuitive ; en
pratique, cependant, c’est une troisième méthode qui va nous permettre de
traduire cette notion sous forme analytique. Nous supposons donc donnée
sur l’espace fibré principal P = P(M,G) une distribution horizontale
équivariante. La forme de connexion ω est une forme sur P et à valeurs dans
l’algèbre de Lie 𝔤 du groupe structural (nous verrons que cette forme doit, en
outre, être équivariante). Elle est définie comme suit. Soit e un élément
de P (un repère de M), et Xα une base de Lie(G). Nous décomposons
l’espace tangent T(P,e) en un sous espace vertical Tv(P,e) = V (P,e)
engendré par les champs fondamentaux 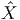 α et un sous espace horizontal
Th(P,e) = H(P,E) défini par la donnée de la distribution horizontale. On
pose
α et un sous espace horizontal
Th(P,e) = H(P,E) défini par la donnée de la distribution horizontale. On
pose
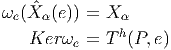
Ainsi donc, on peut décomposer tout vecteur V ∈ T(P,e), comme suit :
V = V α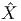 α(e) + V h avec V h ∈ H(P,e) et ω(V ) = V αX
α. La forme ω est donc
bien définie. Sa signification est claire : si on effectue un déplacement
infinitésimal du repère e (sans changer l’origine), on associe à ce déplacement la
rotation infinitésimale V αX
α correspondante ; si, au contraire, on effectue un
déplacement infinitésimal du repère e en déplaçant l’origine mais sans faire
“tourner” le repère, on obtient ω(V ) = 0. Bien évidemment, on peut analyser les
choses différemment en décidant que la connexion est définie par la forme de
connexion ω, la rotation du repère e lors d’un déplacement infinitésimal V
étant précisément mesurée par la rotation infinitésimale ω(V ) et ceci
donne alors un sens au verbe “tourner”. La distribution horizontale étant
équivariante, il s’ensuit que les noyaux de ω en e et en eg,g ∈ G sont reliés
par
α(e) + V h avec V h ∈ H(P,e) et ω(V ) = V αX
α. La forme ω est donc
bien définie. Sa signification est claire : si on effectue un déplacement
infinitésimal du repère e (sans changer l’origine), on associe à ce déplacement la
rotation infinitésimale V αX
α correspondante ; si, au contraire, on effectue un
déplacement infinitésimal du repère e en déplaçant l’origine mais sans faire
“tourner” le repère, on obtient ω(V ) = 0. Bien évidemment, on peut analyser les
choses différemment en décidant que la connexion est définie par la forme de
connexion ω, la rotation du repère e lors d’un déplacement infinitésimal V
étant précisément mesurée par la rotation infinitésimale ω(V ) et ceci
donne alors un sens au verbe “tourner”. La distribution horizontale étant
équivariante, il s’ensuit que les noyaux de ω en e et en eg,g ∈ G sont reliés
par
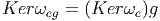 Ici
encore, l’application tangente est simplement notée g.
Ici
encore, l’application tangente est simplement notée g.
Nous reviendrons un peu plus loin (en 4.3.6) sur la théorie des connexions
dans les fibrés principaux mais nous allons, pour des raisons aussi bien
pédagogiques (c’est plus simple !) que pratiques (on mène en général
les calculs sur la base), passer à une expression locale de la forme de
connexion, puis, à partir de là, développer la théorie dans les fibrés vectoriels
associés.
4.1.5 Ecriture locale de la forme de connexion : le potentiel de
jauge
Le fait que tout fibré principal soit localement trivial va nous permettre -
moyennant le choix d’une section locale - d’écrire la forme de connexion ω, non
pas comme une forme sur P à valeurs dans 𝔤 mais comme une forme sur M à
valeurs dans 𝔤. Choisissons donc une section locale M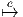 P et notons
de : TM
P et notons
de : TM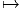 TP l’application linéaire tangente. Rappelons que, si P est un fibré de
repères, la section locale e(x) n’est autre qu’un repère mobile e(x) = (eμ(x))
défini dans le domaine d’un certain ouvert et que, dans le cas où P désigne le
fibré des repères d’un certain “espace interne” (terminologie utilisée en physique
des particules) on dira plutôt que e(x) est un choix de jauge. Supposons qu’on
s’est fixé une connexion caractérisée par la forme de connexion ω, on défini le
potentiel de jauge A
TP l’application linéaire tangente. Rappelons que, si P est un fibré de
repères, la section locale e(x) n’est autre qu’un repère mobile e(x) = (eμ(x))
défini dans le domaine d’un certain ouvert et que, dans le cas où P désigne le
fibré des repères d’un certain “espace interne” (terminologie utilisée en physique
des particules) on dira plutôt que e(x) est un choix de jauge. Supposons qu’on
s’est fixé une connexion caractérisée par la forme de connexion ω, on défini le
potentiel de jauge A
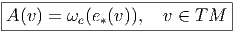 où
e* ≡ de désigne l’application tangente à la section locale e.
où
e* ≡ de désigne l’application tangente à la section locale e.
A est donc une 1-forme sur M à valeurs dans 𝔤. Soit {Xα} une base de 𝔤 et
{∂∕∂xμ} une carte locale sur M, on pourra écrire :
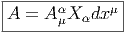
En fait, il faudrait noter cet objet eA et non pas A de façon à se rappeler du
fait que la définition de A dépend du choix de la section locale e mais on omet
généralement d’y faire référence. Par contre, il est très important de savoir
comment se transforme A lorsqu’on effectue un choix différent. Posant A = eA et
A′ = e′A, et supposant que e′(x) = e(x).g(x) avec g(.) : M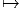 G, nous verrons un
peu plus loin que la propriété d’équivariance de ω se traduit pour A, par la
propriété suivante :
G, nous verrons un
peu plus loin que la propriété d’équivariance de ω se traduit pour A, par la
propriété suivante :
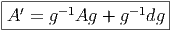
Pour finir, notons qu’en pratique les calculs sont effectués sur la base M et
non sur le fibré P ; en d’autres termes on préfère utiliser le potentiel de
jauge A plutôt que la forme de connexion ω, quitte à devoir recoller les
morceaux puisque le fibré P considéré n’est pas en général trivial et qu’il
faut donc définir A sur toutes les cartes d’un atlas de M. Le potentiel de
jauge A est quelquefois désigné sous le nom “pull back de la forme de
connexion” et il possède des interprétations physiques variées, dépendant,
bien sûr, de la nature du fibré principal P (et donc du groupe structural
G). Citons quelques unes de ces interprétations ainsi que la terminologie
correspondantes :
G = U(1), A est le potentiel électromagnétique (ou champ de photons)
G = SU(3), A est le potentiel chromodynamique (ou champ de gluons)
G = SU(2) × U(1), A est le potentiel du champ électro-faible (champ des
bosons γ, W± et Z).
Dans le cas des théories gravitationnelles où G désigne GL(n) et plus
généralement un groupe de changement de repères d’une variété de dimension n,
on parle plutôt de “symboles de Christoffel” pour désigner les composantes de A ;
nous y reviendrons dans la section consacrée aux connexions linéaires.
Le lecteur aura compris (chose qu’il sait sans doute depuis longtemps) que les
potentiels de jauge -et la théorie des connexions en général - permettent
de représenter mathématiquement toutes les forces fondamentales de la
physique.
 au
point
au
point 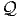 sur la base, et à tout repère au point
sur la base, et à tout repère au point  , un certain chemin dans
l’espace des repères. Choisir d’une telle méthode revient précisément à
choisir ce qu’on appelle une connexion dans le fibré principal des repères
linéaires. Le mot “connexion” – en anglais “connection”– est bien choisi
puisqu’il nous permet effectivement de connecter (de comparer) des vecteurs
(plus généralement des éléments d’un fibré associé) situés en des points
différents de la variété. Le cas de l’espace affine Rn est très particulier
puisqu’on peut disposer là de repères globaux permettant de comparer
des vecteurs situés en des points différents ; il existe d’autres variétés
pour lesquelles cette propriété est également valable et où le choix d’un
repère mobile global est possible : ce sont les variétés parallèlisables déjà
mentionnées dans le chapitre précédent. Nous allons, dans un premier
temps, définir la notion de connexion de façon infinitésimale, comme
étant un moyen d’associer un déplacement infinitésimal dans l’espace des
repères à un déplacement infinitésimal du point de base (c’est à dire du
point où le repère est situé). En fait, la seule structure utilisée dans la
définition de la notion de connexion est celle de fibré principal et tout ce
qu’on écrira aura encore un sens si on remplace le fibré des repères par un
fibré principal quelconque (cela dit, il est bien commode de visualiser les
choses en utilisant des repères, nous nous permettrons donc d’utiliser
le mot “repère” pour désigner un élément d’un espace fibré principal
quelconque).
, un certain chemin dans
l’espace des repères. Choisir d’une telle méthode revient précisément à
choisir ce qu’on appelle une connexion dans le fibré principal des repères
linéaires. Le mot “connexion” – en anglais “connection”– est bien choisi
puisqu’il nous permet effectivement de connecter (de comparer) des vecteurs
(plus généralement des éléments d’un fibré associé) situés en des points
différents de la variété. Le cas de l’espace affine Rn est très particulier
puisqu’on peut disposer là de repères globaux permettant de comparer
des vecteurs situés en des points différents ; il existe d’autres variétés
pour lesquelles cette propriété est également valable et où le choix d’un
repère mobile global est possible : ce sont les variétés parallèlisables déjà
mentionnées dans le chapitre précédent. Nous allons, dans un premier
temps, définir la notion de connexion de façon infinitésimale, comme
étant un moyen d’associer un déplacement infinitésimal dans l’espace des
repères à un déplacement infinitésimal du point de base (c’est à dire du
point où le repère est situé). En fait, la seule structure utilisée dans la
définition de la notion de connexion est celle de fibré principal et tout ce
qu’on écrira aura encore un sens si on remplace le fibré des repères par un
fibré principal quelconque (cela dit, il est bien commode de visualiser les
choses en utilisant des repères, nous nous permettrons donc d’utiliser
le mot “repère” pour désigner un élément d’un espace fibré principal
quelconque).