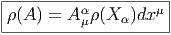
Soit A = AμαX αdxμ le potentiel de jauge définissant une forme de connexion ω sur le fibré principal P = P(M,G) et soit E = P ×ρV un fibré vectoriel associé à P via la représentation ρ sur l’espace vectoriel V de dimension p. En utilisant la représentation ρ nous allons représenter le potentiel de jauge lui-même et obtenir ainsi une notion de connexion pour tout fibré vectoriel associé. Soit {Xα}α∈{1,dim(G)}, une base de 𝔤. Nous désignerons encore par ρ la représentation de 𝔤 correspondant à celle de G ; ainsi ρ(Xα) = (ρ(Xα)ji) est une matrice p × p décrivant un endomorphisme de l’espace vectoriel V .
Dans ce paragraphe nous noterons :
μ,ν,ρ… les indices de base (variété M de dimension d)
i,j,k… les indices de fibre (espace vectoriel V de dimension p)
α,β,γ… les indices d’algèbre de Lie (LieG de dimension n)
L’image ρ(A) du potentiel de jauge par la représentation ρ s’appelle la matrice de connexion
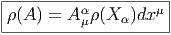
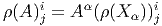
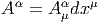
La représentation ρ étant choisie une fois pour toutes (le fibré vectoriel E étant choisi) on peut omettre le symbole ρ lui-même, et si nous posons
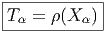
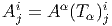
Ses éléments de matrice sont des 1-forme puisque
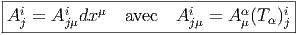
Les nombres Ajμi sont les coefficients de connexion . Revenons une fois de plus sur ces problèmes de notations, de terminologie et d’habitudes : les physiciens des particules utilisent les Aμα, les spécialistes de la gravitation préfèrent les A jμi (la relation précédente permettant de faire le lien entre les deux) ; ces derniers ont d’ailleurs l’habitude de noter Γ (plutôt que A) les coefficients de connexion, ils utilisent donc des Γjμi, les indices ji étant les indices de fibre et μ l’indice de forme. Là où les choses se compliquent, c’est que le fibré E peut désigner le fibré tangent TM et que, dans ce cas, les indices de fibre peuvent appartenir au même jeu d’indices que les indices de forme (on a donc des objets Γρμν) mais il faut toujours se rappeler qui est qui. Les conventions, comme d’habitude, n’étant pas universelles, le lecteur est prié de se rappeler que, pour nous, l’indice de base c’est à dire encore l’indice de forme (noté μ ci-dessus) est situé en bas, et en dernière position. Nous reviendrons un peu plus loin sur le cas particulier E = TM (connexions linéaires). En attendant, il convient de se rappeler que, dans la notation Ajμi, l’indice μ se réfère au choix d’un repère naturel associé à une carte (eμ = ∂ __ ∂xμ) ou d’un repère mobile quelconque ([eμ,eν] = fμνρe ρ) et que les indices i,j se réfèrent au choix d’une base (ei(x)) dans la fibre de E située au point x de M.
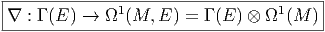
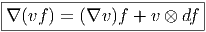
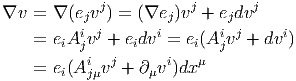
Une section v est dite parallèle (ou transportée par parallélisme) lorsque ∇v = 0
Puisque ∇v possède un indice de forme (c’est un élément de Γ(E) ⊗ Ω1(M)), on peut l’évaluer sur les vecteurs tangents. Soit ξ = ξμ∂ μ un vecteur tangent. La dérivée covariante de v dans la direction ξ se note ∇ξv et s’obtient en évaluant ∇v sur ξ :
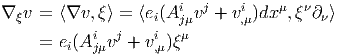
Notons que ∇ξv, ainsi que v, est une section de E alors que ∇v est une section-1-forme. On note souvent v;μi les composantes de ∇ μv = ∇ ∂__ ∂xμ v par rapport au repère {ei} de la fibre :
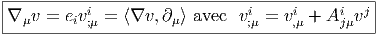
Nous attirons l’attention du lecteur sur le fait que la moitié des physiciens n’utilisent que des objets “indexés”. Ces derniers ne considèrent jamais ni v ni ∇μv mais seulement leurs composantes vi et v ;μi. Cette habitude n’entraîne généralement aucune confusion. Par contre, cela devient un problème si on décide, simultanément, d’utiliser également la notation ∇μ et de décider que ∇μvi est un synonyme de v ;μi. Nous estimons qu’il s’agit là d’un abus de notations particulièrement dangereux pouvant facilement conduire à des erreurs. En effet, vi est une composante de v, c’est à dire une fonction de x ; sa dérivée covariante existe bien, mais, puisqu’il s’agit d’une simple fonction, elle est égale à sa dérivée ordinaire, ainsi ∇μvi = ∂ μvi = v ,μi, ce qui n’est pas du tout égal à v ;μi. Si le lecteur ne souhaite pas manipuler des objets comme v ou ∇μv mais seulement leurs composantes, nous lui suggérons très fortement de se contenter de la notation “point-virgule”.
Lors de la définition de ∇ei = ejAij en 4.2.2, le lecteur a pu être surpris de l’absence du signe de produit tensoriel entre le vecteur ej qui est une section locale du fibré vectoriel considéré et la 1-forme Aij qui est une section locale du fibré cotangent T*M (puisque A ij = A iμjdxμ).
Un peu plus loin, le lecteur a pu être de nouveau surpris, lors du calcul de ∇v et de ∇ξv, car nous avons allègrement commuté les formes sur M (par exemple eμ = dxμ) et les sections de E (les e i).
Mis à part le fait qu’il existe un isomorphisme canonique entre Γ(E) ⊗ Ω1(M) et Ω1(M) ⊗ Γ(E) et que le produit tensoriel utilisé est un produit au dessus de C∞(M) et non au dessus de I R, les manipulations précédentes, sur lesquelles nous ne nous étendrons pas, sont justifiées par le fait qu’il est possible de remplacer, dans la plupart des calculs de géométrie différentielle, l’algèbre commutative C∞(M) par l’algèbre commutative graduée Ω(M).
Les espaces E et T*M étant, en général bien distincts, nous décidons d’identifier par exemple dxμe i ⊗ ej… et ei ⊗ ej…dxμ et nous n’utiliserons pas de symbole de produit tensoriel entre les p-formes sur M et les sections de E, traitant ainsi les dxμ comme des fonctions. Par ailleurs nous écrirons toujours les formes “en dernier”.
Cette identification nous permet d’écrire aussi bien
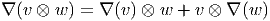
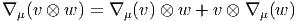
Il existe cependant un cas particulier où il existe une confusion possible entre les fibrés E et T*M, c’est précisément le cas où on choisit E = T*M. Dans ce cas, il faut se rappeler “qui est qui”, c’est à dire quels sont les indices de forme et quels sont les indices de fibre. Cette possible identification permet en fait d’enrichir la théorie. Nous y reviendrons.
Soient e = (ei) et e′ = (e i′′) deux repères dans les fibres. L’un s’obtient à partir de l’autre par une transformation linéaire Λ :
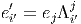
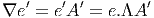
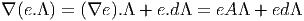
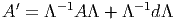
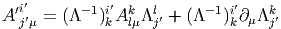
On obtient alors immédiatement
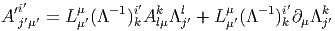
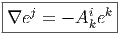
Après avoir défini ∇ sur les sections de E grâce à la relation ∇ei = ejAij, {ei(x)} désignant une base de la fibre au point x, nous considérons le fibré dual E* et l’action de ∇ sur ses sections. Désignons respectivement par σ et v une forme différentielle et un champ de vecteurs, on aura : ∇⟨σ,v⟩ = ⟨∇σ,v⟩ + ⟨σ,∇v⟩. Notons {ei(x)} la base duale au point x ; alors ⟨ej,e i⟩ = δji.
La quantité δji est une fonction constante, et donc ∇δ ji = 0. On impose
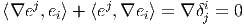
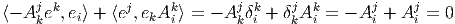
Notre but est ici d’étudier la dérivation covariante des éléments de E⊗p ⊗ (E*)⊗q.
Considérons le fibré vectoriel E ⊗ E, c’est un fibré associé comme un autre... Ses éléments peuvent s’écrire
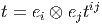
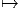ρ(x) ∈ EndV sur l’espace
vectoriel V , il agit via ρ(x) ⊗ 1 + 1 ⊗ ρ(x) sur l’espace vectoriel V ⊗ V , d’où il
s’ensuit que l’opérateur ∇ vérifie la propriété
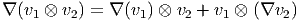
On écrira par exemple, pour t = ei ⊗ ejtij,
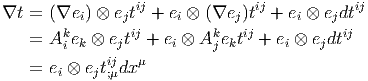
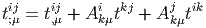
Voici un dernier exemple : Soit t ∈ E ⊗ E ⊗ E*,
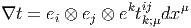
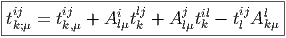
La dérivée covariante d’un tenseur quelconque t = ei ⊗ ej…ek ⊗ el…t kl…ij… dans la direction du champ de vecteurs eμ est définie par
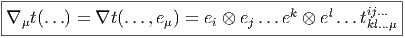
On introduit le symbole D sur l’exemple suivant : prenons
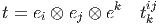
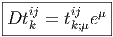
Il faut bien voir que tkij est ici considéré comme une zéro-forme sur le fibré principal P à valeurs dans un espace vectoriel (la fibre type du fibré vectoriel approprié).
Il est facile de généraliser cette notation Dtkij au cas où l’objet considéré n’est pas une 0-forme à valeurs dans un espace vectoriel mais une p-forme à valeurs dans un espace vectoriel.
Il n’existe pas de de convention d’écriture qui soit universelle, pour désigner cet opérateur. Certains auteurs, par exemple, le notent d(gras). Même remarque d’ailleurs pour l’opérateur de différentielle extérieure covariante d∇ défini ci-dessous, que certains auteurs notent souvent… D !
Soit E = E(M,F) un fibré vectoriel ; on a défini ∇ comme un opérateur :
ΓE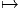
ΓE ⊗ Ω1(M) ; on définit maintenant d∇ comme l’unique opérateur
prolongeant ∇ comme dérivation graduée de l’algèbre ⊕
pE ⊗ Ωp(M). Ainsi
donc
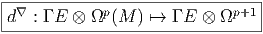
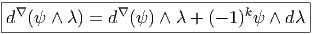
Le lecteur peut, à juste titre, se demander pourquoi nous distinguons les deux notations d∇ et ∇. La raison en est la suivante : nous réservons la notation ∇ au cas où l’on agit sur une 0-forme. En effet, il est des cas où un objet mathématique donné peut être considéré soit comme une p-forme à valeurs dans un certain fibré, soit comme une 0-forme à valeurs dans un fibré différent. Ecrire ∇ω signifie (pour nous) “ω est une 0-forme à valeurs dans un certain fibré vectoriel (c’est à dire une section de ce dernier) et nous calculons sa différentielle extérieure covariante, qui est donc une 1-forme à valeurs dans le même fibré”. Cette distinction que nous opérons, au niveau des notations, permet d’éviter des confusions possibles, en particulier lorsque le fibré E peut désigner le fibré tangent, son dual, ou une puissance tensorielle de ces derniers.
Complément concernant la notation D introduite plus haut :
Si V est, par exemple, un élément de Γ(E ⊗E*⊗E*)⊗Ω2(M) = Ω2(M,E ⊗E*⊗E*), c’est à dire
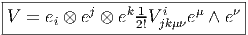
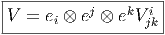
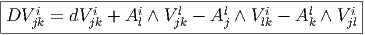
En effet :
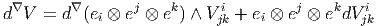
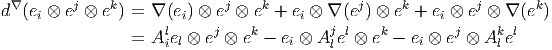
A titre d’exercice, calculons d∇u où u est un élément de ΓE ⊗ Ω1(M). On choisit un repère (ei) dans ΓE et un repère (eμ) dans Ω1(M) il peut s’agir d’un corepère naturel par rapport à une carte (eμ = dxμ) ou d’un corepère mobile quelconque eμ avec deμ = -1 2fνρμeν ∧ eρ. On écrit donc u = e iui μeμ. L’ordre des symboles n’a pas trop d’importance —tout au moins en géométrie commutative !— mais nous suggérons fortement au lecteur d’adopter cette écriture, c’est à dire l’ordre 1)2)3) avec 1), un élément de ΓE, 2), un coefficient, c’est à dire un élément de l’algèbre (commutative) C∞(M) des fonctions sur M, et 3), une p-forme. Le lecteur aura sans doute également noté que, conformément à nos habitudes, nous avons omis d’écrire explicitement le symbole ⊗ du produit tensoriel entre les sections de E (les ei) et les p-formes (ici, les eμ).
La première méthode permettant de calculer d∇u est d’utiliser la règle de dérivation généralisée qui définit l’opérateur d∇ :
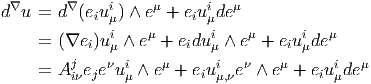
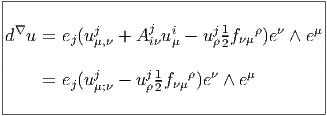
La deuxième méthode pour calculer d∇u n’est pas vraiment une méthode puisqu’elle revient à utiliser une formule générale. Posons u = eiui en ne faisant pas apparaître explicitement l’indice de forme dans l’expression de u, bien que ui = u μieμ. On écrit immédiatement (voir l’expression “modèle” de DV jki donnée précédemment)
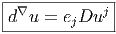
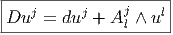
Une forme extérieure de degré p à valeurs dans un fibré vectoriel E peut, bien sur, être évaluée sur p vecteurs v1,v2,…,vp tangents à M. Par exemple, si u ∈ Ω1(M,E), en évaluant d∇u ∈ Ω2(M,E) sur deux vecteurs v 1 et v2, on obtient
![|∇--------------------------------------------|
d--u(v1,v2) =-∇v1u-(v2) --∇v2u-(v1) --u([v1,v2])](source592x.png)
en effet,
![∇ j j1- μ ν μ
d u(eσ,e τ) = ej(u μ;ν - uρ2 fνρ )e ∧ e (eσ,eτ)
1
= ej(ujμ;ν - ujρ--fνρμ)(δνσδτμ- δμσ δντ)
2
= ej(uj - uj - ejuj 1(fστρ - fτσρ))
τ;σ σ;τ ρ2
= ej((ujτ;σ - ujσ;τ) - ujρfστρ)
= ∇eσu (e τ) - ∇e τu(eσ) - u([eσ,eτ])](source593x.png)
Plus généralement, si u ∈ Ωp(M,E),
![∇ p+1 i+1
d u (v1,v2,...,vp+1) = Σi=1(- 1) ∇viu(v1,...,vˆi,...,vp+1) +
Σ1≤i≤j≤p+1(- 1)i+ju ([vi,vj],v1,...,ˆvi,...,ˆvj,...,vp+1)](source594x.png)
Pour conclure cette section, nous attirons l’attention du lecteur sur le fait que, malgré la notation utilisée, le carré de l’opérateur d∇ n’est pas nul. C’est d’ailleurs la présence d’un second membre non nul dans l’équation (d∇)2 = F qui va nous permettre un peu plus loin de définir l’opérateur de courbure.
La différentielle covariante ∇σ d’un élément de ΓE est un élément de ΓE ⊗ Ω1(M). En général, les fibrés E et TM sont distincts (sauf dans le cas particulier 4.4). Il n’empêche que Ω1(M) peut être considéré comme l’ensemble des sections de T*M, et, qu’en conséquence, cet élément ∇σ, au lieu d’être considéré comme une 1-forme à valeurs dans le fibré vectoriel E peut être considéré comme une 0-forme à valeurs dans le fibré vectoriel T*M ⊗ E, c’est à dire un élément de Γ(T*M ⊗ E). Nous désignerons en général par le symbole Ωp(X,Y ) l’ensemble des p-formes sur X à valeurs dans Y . Avec ces notations, nous voyons qu’il est possible d’identifier Ω1(M,E) et Ω0(M,T*M ⊗ E).
Jusqu’à présent, la connexion (le potentiel de jauge Aji = A jμidxμ) avait trait au fibré E, mais il peut se faire…(et généralement il se fait) que T*M lui-même soit muni d’une connexion (un potentiel de jauge Γρν = Γ ρμνdxμ). Nous étudierons plus loin, et en détails, le cas particulier des connexions linéaires (du type Γρμν), mais dans le présent paragraphe, nous souhaitons seulement attirer l’attention du lecteur sur l’existence d’une ambiguïté (le fait qu’une 1-forme à valeurs dans un fibré puisse aussi être considérée comme une 0-forme à valeurs dans un fibré différent) et sur le fait que cette ambiguïté permet, en quelque sorte, d’enrichir la théorie. Reprenons l’exemple de σ ∈ Γ(E) ; on a u = d∇σ = ∇σ ∈ Ω1(M) ⊗ Γ(E). En tant que 1-forme à valeurs dans le fibré vectoriel E, nous pouvons faire appel à la théorie des différentielles extérieures covariantes et calculer d∇u = (d∇)2σ, qui est un élément de Γ(E) ⊗ Ω2(M). Cependant, en considérant u comme une 0-forme à valeurs dans le fibré T*M ⊗ E, nous pouvons — dans la mesure où les deux fibrés E et T*M sont équipés de connexions — calculer la différentielle covariante ∇u = ∇∇σ. Lorsque σ ∈ Γ(E), le calcul de ∇σ ne fait appel qu’à la connexion Aji, mais celui de ∇u (avec u = ∇σ) fait appel simultanément à la connexion Aji sur E et à la connexion Γνμ sur T*M. Plus généralement, si u désigne un objet ayant un certain nombre (p,q) d’indices de type E (ou E*) et un certain nombre (p′,q′) d’indices de type TM (ou de type T*M), nous pouvons le considérer comme une 0-forme à valeurs dans TMp′,q′⊗ Ep,q, et calculer ∇u, qui sera un élément de Γ(TMp′,q′⊗ Ep,q) ⊗ Ω1(M). Nous pouvons aussi, dans le cas où u est antisymétrique en s indices de forme (s indices de type T*M), considérer u comme un élément de Γ(TMp′,q′-s ⊗ Ep,q) ⊗ Ωs(M) et calculer sa différentielle extérieure covariante d∇u qui sera un élément de Γ(TMp′,q′-s ⊗Ep,q) ⊗ Ωs+1(M). On imagine aisément la richesse des possibilités… Au niveau des notations, nous adoptons la convention suivante : si on écrit ∇u, c’est que u doit être considéré comme une 0-forme dans un fibré approprié (même si u = ∇σ) ; par contre, si on écrit d∇u, c’est que u doit être considéré comme une p-forme sur M et que d∇ est une différentielle extérieure covariante. En d’autres termes, l’utilisation de d∇ conduit toujours à des objets possédant une certaine antisymétrie, ce qui n’est pas le cas pour ∇. Il est bien évident que ces notations sont insuffisantes pour couvrir tous les cas possibles, mais en général le contexte devrait permettre de préciser.
Soit u = eiuμieμ ∈ ΓE ⊗ Ω1(M). En tant que tenseur-1-forme, on écrira plutôt u = eiui sans faire apparaître explicitement l’indice de forme ; on a déjà calculé sa différentielle extérieure covariante
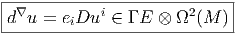
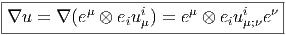
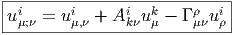
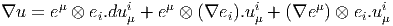
Par ailleurs,
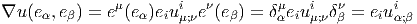
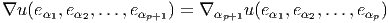
Notons que, conformément à nos conventions, nous avons écrit les vecteurs de base (les eμe i ≡ eμ ⊗e i) à gauche des composantes (les uμi) et la base des 1-formes (les eν) à droite des composantes.
On pourra utilement comparer l’expression de ∇u obtenue ci-dessus avec celle de d∇u calculée auparavant :
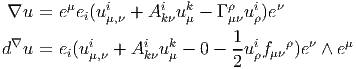
On voit que d∇u = -2Alt∇u ou Alt désigne l’opérateur d’antisymétrisation. De façon générale, si u ∈ Ωp(M,E), on peut fabriquer d∇u ∈ Ωp+1(M,E) ou ∇u ∈ Γ(T*pM ⊗ E) ⊗ Ω1(M) ≡ Ω1(M,T*pM ⊗ E) ; la relation entre les deux est
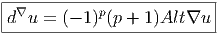
Notons enfin que d∇ ne fait explicitement intervenir que la connexion A sur E
alors que ∇ fait appel à la fois à la connexion A sur E et à la connexion Γ sur
TM. Il existe un cas particulièrement intéressant où les fibrés E et TM
co
incident ; nous y reviendrons dans la section consacrée aux connexions
linéaires.