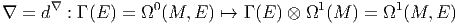
Comme nous l’avons vu, l’opérateur
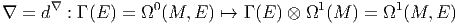
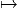 Ωp+1(M,E) et vérifie la propriété
Ωp+1(M,E) et vérifie la propriété
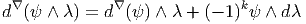

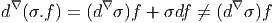
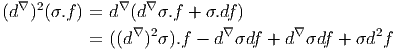
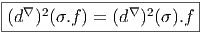
Cette propriété de linéarité est absolument fondamentale. C’est elle qui, en définitive, est responsable du fait que la courbure est caractérisée par un tenseur. Par ailleurs, le fait que (d∇)2 envoie Γ(E) dans Γ(E) ⊗ Ω2(M) montre que, si on “gèle” les indices de forme (correspondant à l’espace Ω2(M)), cet opérateur envoie —linéairement— les sections de E dans les sections de E. En d’autres termes (d∇)2 peut être considéré comme une 2-forme à valeurs dans le fibré des endomorphismes de E.
Remarque : On peut directement définir la courbure sur un fibré principal en restant “dans le fibré principal” c’est à dire sans avoir besoin de se placer sur la base et sans même considérer les fibrés associés. Une telle définition, dans la lignée de celle donnée en section 4.2.1, peut alors se transporter au niveau des différents fibrés vectoriels associés, grâce au choix de la représentation définissant le fibré en question. Il s’agit là d’une méthode élégante mais un peu abstraite en première lecture … Nous y reviendrons un peu plus loin (cf. paragraphe 4.3.6). En attendant, nous préférons définir la courbure plus simplement, dans chaque fibré associé, en utilisant les résultats déjà obtenus pour l’écriture de la dérivée covariante et de la différentielle extérieure covariante.
Nous venons de voir que le carré de la différentielle extérieure covariante est un opérateur (en général non nul !) qui est linéaire par rapport aux fonctions sur la variété. Appliqué a une section d’un fibré vectoriel E, il lui fait correspondre une 2-forme (sur la base M) à valeurs dans E ; l’écriture locale de cet opérateur fera donc appel a deux jeux d’indices différents : des indices μ et ν en position basse, parce qu’il s’agit d’une 2-forme, et deux indices i et j, l’un en position haute et l’autre en position basse, en effet, les indices de forme étant fixés, l’opérateur agit comme un endomorphisme de la fibre (il transforme les sections en sections). Cet objet est, de surcroît, antisymétrique par rapport aux indices de forme μ et ν puisqu’il s’agit... d’une 2-forme ! La donnée de cet opérateur fera donc intervenir n(n - 1)∕2 + p2 nombres F jμνi si on suppose que dimM = n et que la fibre type est un espace vectoriel de dimension p.
L’objet fabriqué peut être considéré de bien des façons. En effet, si on gèle les indices de forme, on obtient Fμν qui est une matrice p × p dont les éléments de matrice sont les Fji μν. Si par contre, on gèle les indices de fibre, on obtient Fji qui est une 2-forme sur la base. Nous verrons même un peu plus loin encore d’autres façons de considérer cet objet. Certains auteurs réservent des notations différentes pour ces objets qui sont mathématiquement distincts. Nous ne le ferons pas car ne pas vouloir commettre de tels abus de notations nuit, à notre avis, à la compréhension. Chaque fois qu’on a un tenseur appartenant à un espace vectoriel E ⊗ F ⊗ G, on peut le considérer comme un élément de Hom((E ⊗ F ⊗ G)*, lC) ou comme un élément de Hom(E*,F ⊗ G) ou comme … Cela ne nous semble pas raisonnable de vouloir, à chaque fois, changer la notation désignant l’objet en question !
Nous poserons donc simplement
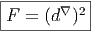
Nous calculons maintenant l’expression de l’opérateur de courbure F en terme de la connexion A. Soit ei une famille de sections (locales ou non) constituant, en chaque point x d’un certain voisinage de la base M une base de la fibre V x au dessus de x. On sait que (d∇)2 : ΓE = Ω0(M,E) → Ω2(M,E). On va calculer
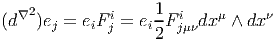
Il vient :
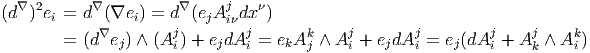
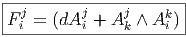
Il existe essentiellement deux façons d’exprimer l’opérateur de courbure. la première, en fonction des coefficients de connexion (potentiels de jauge) est celle que nous venons de voir. La seconde, baptisée “équation de structure” exprime directement la courbure en fonction de l’opérateur de dérivée covariante. A titre d’exercice préliminaire, nous avons déjà calculé explicitement les composantes de la différentielle extérieure covariante d∇σ d’une 1-forme σ à valeurs dans un fibré vectoriel E. Soit {eμ} un co-repère mobile (base constituée de sections locales de T*M) et {e i} un repère local du fibré E (base constituée de sections locales de E). Soit σ ∈ Ω1(M,E). On peut donc écrire σ = e iσμieμ. Nous avons déjà vu que
![∇
d σ(eσ,eτ) = ∇ σσ (eτ) - ∇ τσ(eσ) - σ([eσ,eτ])](source615x.png)
Supposons maintenant que la 1-forme σ, à valeurs dans E soit elle-même obtenue comme la différentielle d’une section v de E : σ = ∇v. Dans ce cas (d∇)2v = d∇σ. Nous utilisons le calcul précédent ; il vient
![(d∇ )2v (eμ, eν) = d∇σ (e μ,eν)
= ∇ σ(e ) - ∇ σ (e ) - σ ([e ,e ])
μ ν ν μ μ ν
= ∇ μ∇ νv - ∇ ν∇ μv - ∇ [μ,ν]v](source616x.png)
Mais, par définition,
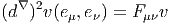
![|-----------------------|
|Fμν = [∇ μ,∇ ν] - ∇ [μ,ν]
------------------------](source618x.png)
Cette identité, désignée souvent sous le nom de deuxième identité de Bianchi (nous verrons la “première” dans le chapitre consacré aux connexions linéaires) est une identité satisfaite par l’opérateur de courbure. Elle s’obtient en utilisant la définition de F = dA + A∧A et les propriétés élémentaires suivantes : d2 = 0 et A ∧ (A ∧ A) = (A ∧ A) ∧ A.
Tout d’abord F = dA + A ∧ A ⇒ dF = d2A + dA ∧ A - A ∧ dA. On utilise alors une deuxième fois la définition de F en remplaçant dA par F - A ∧ A dans la dernière expression. Il vient dF = 0 + (F - A ∧ A) ∧ A - A ∧ (F - A ∧ A), d’où
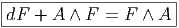
On peut écrire explicitement les indices de forme : voir page 396.
Notons que, lorsque le groupe structural est abélien, A ∧ F - F ∧ A = 0 puisque ces formes sont à valeurs réelles. L’identité de Bianchi s’écrit alors simplement dF = 0, ce qui nous donne la “moitié” des équations de Maxwell décrivant le champ électromagnétique (celles qui ne font pas intervenir les sources). Dans le cas non abélien, et dans le contexte de l’étude des particules élémentaires (par exemple dans l’étude du champ chromodynamique), la même équation de Bianchi nous donne la “moitié” des équations de Yang-Mills (celles qui ne font pas intervenir les sources).
Soit ω une forme de connexion sur un fibré principal P et Ω = Dω la forme de courbure correspondante. Nous avons vu que la définition du potentiel de jauge A et de la courbure F faisait appel au choix d’une section locale
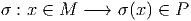

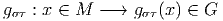
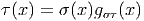
Nous avons étudié au 4.2.4 comment se transformaient les potentiels de jauge par changement de section, à savoir,
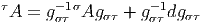
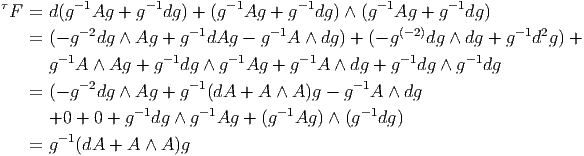
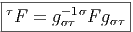
Nous avons tout d’abord défini la forme de connexion ω au niveau de fibré principal, puis le potentiel de jauge Aμα sur la base (A n’est rien d’autre qu’une écriture locale de ω), puis nous avons défini la matrice de connexion Ajμi dans chaque fibré associé. Il est possible d’adopter une démarche similaire pour la courbure associée à une connexion : il est possible de définir une 2-forme de courbure Ω au niveau du fibré principal, puis son écriture locale Fμνα sur la base, puis enfin le tenseur Fji μν = Fμναρ(X α)ji dans chaque fibré associé caractérisé par une représentation ρ du groupe structural. Bien entendu, l’objet ainsi obtenu doit coïncider avec la courbure introduite et étudiée dans les sous-sections précédentes où nous avons travaillé tout du long dans les fibrés vectoriels. Cela dit, nous avons préféré, dans le cadre de cet ouvrage, pour des raisons d’ordre aussi bien pédagogiques que pratiques, développer le formalisme de la courbure dans les fibrés vectoriels. Nous allons néanmoins énoncer quelques définitions et résultats généraux, de façon à ce que lecteur se fasse une idée de ce qu’aurait pu être une autre façon de présenter le sujet. Nous laissons au lecteur le soin de démontrer l’équivalence des différentes approches.
Compléments sans démonstration. Soit P = P(M,G) un fibré principal muni
d’une forme de connexion ω. Nous savons déjà que les noyaux de ω en e et en
eg,g ∈ G sont reliés par Kerωeg = (Kerωe)g. Par ailleurs, on sait que la
composée de ω avec l’application (Rz)* : LieG T(z,P) qui, à tout élément
de l’algèbre de Lie associe un vecteur tangent en z, doit coïncider avec
l’application identique. On en déduit la loi de transformation suivante pour
ω :
T(z,P) qui, à tout élément
de l’algèbre de Lie associe un vecteur tangent en z, doit coïncider avec
l’application identique. On en déduit la loi de transformation suivante pour
ω :
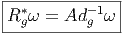
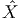 α(z)) = Xα et satisfaisant à la propriété d’équivariance
ci-dessus.
α(z)) = Xα et satisfaisant à la propriété d’équivariance
ci-dessus.
La différentielle covariante sur un fibré principal , que nous noterons D et non ∇
se définit comme suit. Si 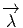 est une p-forme sur P (à valeurs réelles ou complexes,
à valeurs dans un espace vectoriel, ou encore à valeurs dans une algèbre de Lie),
on définit D
est une p-forme sur P (à valeurs réelles ou complexes,
à valeurs dans un espace vectoriel, ou encore à valeurs dans une algèbre de Lie),
on définit D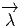 comme la différentielle extérieure (usuelle) de l’horizontalisée de
comme la différentielle extérieure (usuelle) de l’horizontalisée de
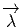 . Cela signifie que pour calculer D
. Cela signifie que pour calculer D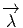 (w1,w2,…,wp,wp+1) on évalue la
différentielle d
(w1,w2,…,wp,wp+1) on évalue la
différentielle d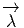 sur l’horizontalisé des vecteurs w1,w2,…,wp+1.
sur l’horizontalisé des vecteurs w1,w2,…,wp+1.
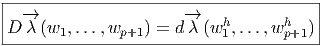
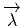 est horizontal, ni qu’il est
équivariant. Lorsque ρ est une représentation du groupe structural G
et que
est horizontal, ni qu’il est
équivariant. Lorsque ρ est une représentation du groupe structural G
et que 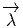 est horizontal et équivariant de type ρ, c’est à dire qu’il est
à valeurs dans l’espace vectoriel support de la représentation ρ et que
est horizontal et équivariant de type ρ, c’est à dire qu’il est
à valeurs dans l’espace vectoriel support de la représentation ρ et que
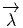 zg(w1,…,wp) = ρ(g-1)
zg(w1,…,wp) = ρ(g-1)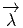 z(w1,…,wp), on démontre que
z(w1,…,wp), on démontre que
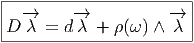
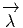 s’annule dès que
l’un de ses arguments est un vecteur vertical : D
s’annule dès que
l’un de ses arguments est un vecteur vertical : D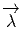 est donc une forme
horizontale.
est donc une forme
horizontale.
Aspect global La 2-forme de courbure sur P, que nous noterons Ω (et non F) est définie très simplement comme
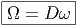
![|-------------------|
|Ω = dω + 12[ω ∧ ω] |
--------------------](source644x.png)
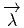 et Dω (présence du facteur 1∕2) car la forme ω est à valeurs dans LieG. Notons
aussi que le résultat obtenu pour
et Dω (présence du facteur 1∕2) car la forme ω est à valeurs dans LieG. Notons
aussi que le résultat obtenu pour 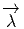 supposait ce dernier horizontal, ce qui n’est
manifestement jamais le cas pour ω.
supposait ce dernier horizontal, ce qui n’est
manifestement jamais le cas pour ω.
Aspect local De la même façon que nous sommes passés de ω, défini sur P à son expression locale, le potentiel de jauge A (la 1-forme définie sur M par A(v) = ω(σ*v)), nous pouvons passer de Ω (défini sur P) à son expression locale, qui est une 2-forme F définie sur M et à valeurs dans LieG. Choisissons en effet une section locale x ∈ M-→σ(x) ∈ P, et v1,v2, deux vecteurs en x. On pose
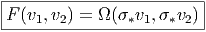
Si v1 et v2 sont deux vecteurs eμ,eν appartenant à un repère mobile {eμ}, on pose Fμν = F(eμ,eν). Cette expression appartient à LieG. Si on choisit une base {Xα} de cette algèbre de Lie, on peut décomposer Fμν sur cette base, et on écrit donc
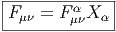
Soit maintenant E = E(M,V ) un fibré vectoriel associé à P via une représentation ρ de G sur un espace vectoriel V de dimension p.
Aspect global La forme de connexion ω, à valeurs dans 𝔤 devient ρ(ω) et, de la même façon, la forme de courbure Ω, à valeurs dans 𝔤 devient ρ(Ω) et est à valeurs dans les endomorphismes de V . On a encore
![1
ρ(Ω ) = ρd(ω) + -[ρ(ω ) ∧ ρ(ω)]
2](source649x.png)
Aspect local Pour obtenir l’expression locale de l’opérateur de courbure, il existe deux possibilités. La première est de transporter l’expression de F, un élément de Ω2(M,𝔤), dans le fibré vectoriel caractérisé par la représentation ρ (il s’agit donc en fait de ρ(F) ∈ Ω2(M,End(V )) mais nous continuerons à le noter abusivement F) en posant
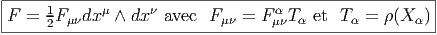
La deuxième possibilité est de représenter localement la 2-forme ρ(Ω). Notons à ce propos que
![Ai ∧ Aj = 1[A ∧ A ]i
j k 2 k](source651x.png)
![Ai ∧ Aj = Aα (T α)i∧ A β(Tβ)j = A α ∧ A β(TαT β)i
j k j k k
= 1(A α ∧ Aβ(T αTβ)i+ Aβ ∧ A α(TβTα)i)
2 k k
1- α β i 1- i
= 2(A ∧ A [Tα,T β]k) = 2[A ∧ A]k](source652x.png)
Ainsi
![F = dA + 1-[A ∧ A] ⇔ F ij = dAij + Aik ∧ Akj
2](source653x.png)
Rappelons une fois de plus que la courbure Ω, dans P, ne dépend que du choix de la connexion, alors que l’objet F qui lui correspond sur la base (ou dans un fibré associé) dépend également du choix d’une section locale σ. Nous notons encore F cet opérateur de courbure, mais un “puriste” rajouterait quelque part les symboles σ et ρ pour se rappeler que la définition dépend de la section locale σ (dépendance “de jauge”) et de la représentation ρ choisie.
Encore une fois, nous laissons au lecteur le soin de démontrer que cette définition de la courbure au niveau des fibrés associés coïncide avec celle donnée dans les sections précédentes.
L’opérateur D2 Les expressions données pour D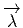 et Dω conduisent à
l’identité de Bianchi que nous avons déjà étudiée auparavant (mais écrite à l’aide
de de F)
et Dω conduisent à
l’identité de Bianchi que nous avons déjà étudiée auparavant (mais écrite à l’aide
de de F)
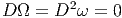
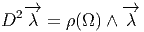
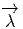 est horizontale et équivariante.
est horizontale et équivariante.
La différentielle covariante D agit sur les formes (n’importe quelles formes)
définies sur le fibré principal P. Certaines de ces formes sont verticales (c’est le
cas de la forme de connexion ω), et les autres sont horizontales (c’est le cas de la
forme de courbure). Par ailleurs, on sait comment associer, à toute p-forme λ sur
M à valeurs dans le fibré vectoriel E, une p-forme 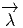 sur P, équivariante, à
valeurs dans la fibre type ; par construction,
sur P, équivariante, à
valeurs dans la fibre type ; par construction, 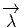 est aussi une forme horizontale.
La différentielle covariante D agit aussi bien sur ω que sur Ω ou
est aussi une forme horizontale.
La différentielle covariante D agit aussi bien sur ω que sur Ω ou 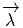 . Cependant,
nous avons déjà introduit un opérateur D agissant sur les sections de fibrés
associés (ou plus généralement sur les sections-p-formes) ainsi que les règles
de calcul correspondantes. Pour un objet équivariant et horizontal, il
est facile de voir que les notations sont compatibles en ce sens que, si
λ = classe((z,
. Cependant,
nous avons déjà introduit un opérateur D agissant sur les sections de fibrés
associés (ou plus généralement sur les sections-p-formes) ainsi que les règles
de calcul correspondantes. Pour un objet équivariant et horizontal, il
est facile de voir que les notations sont compatibles en ce sens que, si
λ = classe((z,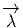 )) alors d∇λ = classe((z.D
)) alors d∇λ = classe((z.D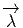 )). Par contre, il est dangereux
d’utiliser la notation D en dehors de ce contexte ; c’est ainsi, par exemple,
que nous nous garderons d’appliquer D (ou d∇) au potentiel de jauge A
lui-même (car il s’agit alors du pull-back, via une section locale, d’une forme
verticale).
)). Par contre, il est dangereux
d’utiliser la notation D en dehors de ce contexte ; c’est ainsi, par exemple,
que nous nous garderons d’appliquer D (ou d∇) au potentiel de jauge A
lui-même (car il s’agit alors du pull-back, via une section locale, d’une forme
verticale).
Nous avons déjà mentionné les diverses façons de considérer cet objet. Nous nous contentons ici de rassembler les diverses notations et formules essentielles. On pose Tα = ρ(Xα).
![F = (d∇)2
F μν = [∇ μ,∇ ν] - ∇ [μ,ν]
F ij = dAij + Aik ∧ Akj ⇔ F = dA + A ∧ A
1
F = -F μνdxμ ∧ dxν
2 α
F μν = FμνT α
F i = F α(T )i
jμν μν α j](source663x.png)
Les physiciens des particules ont l’habitude de développer la courbure sur les générateurs de l’algèbre de Lie, et pour cette raison utilisent le plus souvent les composantes Fμνα. Par contre, les astrophysiciens, cosmologistes et autres spécialistes des phénomènes gravitationnels ont plutôt l’habitude d’utiliser les composantes Fji μν. Le lien entre les deux sortes de notations se fait grâce aux relations précédentes (rappelons que (Tα)ji désigne, dans le repère {ei} du fibré vectoriel, les éléments de matrice (i,j) de la matrice Tα, image du générateur Xα de LieG dans la représentation considérée.
Dans le chapitre précédent, nous avons vu qu’un espace fibré principal P permettait automatiquement de définir une opération de Cartan de l’algèbre de Lie 𝔤 sur l’algèbre différentielle Ω(P) des formes différentielles sur P, c’est à dire un produit intérieur iX et une dérivée de Lie LX, indexés par X ∈ 𝔤 obéissant aux relations usuelles. La seule structure de fibré principal nous a ainsi permis de définir et de caractériser les notions de formes invariantes, horizontales ou basiques.
Nous voulons maintenant généraliser ces opérateurs de façon à ce qu’ils puissent agir sur des formes sur P à valeurs dans une algèbre de Lie 𝔤, c’est à dire sur les éléments de Ω(P,𝔤) = 𝔤 ⊗ Ω(P).
Soit τ ∈ 𝔤 ⊗ Ωs(P) et X ∈ 𝔤, on peut décomposer τ comme une somme de termes du type Y ⊗ α avec Y ∈ 𝔤 et α ∈ Ωs(P). On définit :
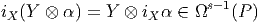
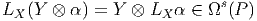
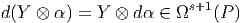
![[Y1 ⊗ α ∧ Y2 ⊗ β ] = [Y1,Y2] ⊗ α ∧ β](source667x.png)
Une connexion algébrique ω sur l’algèbre différentielle Ω(P) est, par définition, la donnée d’un élément de 𝔤 ⊗ Ω1(P) obéissant aux deux conditions suivantes
](source668x.png)
Cette définition est encore valable lorsqu’on remplace Ω(P) par une algèbre différentielle Z Z-graduée quelconque munie d’une opération de Cartan. Nous laissons au lecteur le soin de démontrer que la notion de forme de connexion, telle qu’elle a été définie précédemment coïncide bien avec la notion de connexion algébrique sur Ω(P).
De façon générale, on appelle courbure d’une connexion algébrique la 2-forme Ω à valeurs dans 𝔤 définie par
![Ω = d ω + 1[ω ∧ ω ]
2](source669x.png)

X](source670x.png)
Il s’agit là d’un important sujet mais nous ne ferons que donner quelques définitions générales et énoncer un théorème célèbre.
Soit z un point d’un fibré principal P = P(M,G) qu’on supposera muni d’une connexion ω. Le groupe d’holonomie H(z) de la connexion ω au point z est défini comme suit
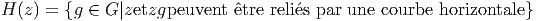
Nous venons de considérer l’ensemble des points de P qui, d’une part, sont situés dans la même fibre que z et qui, d’autre part, peuvent être reliés à z par une courbe horizontale. On peut, de façon plus générale ne pas supposer que ces points sont dans la même fibre. On obtient ainsi la définition du fibré d’holonomie en z :
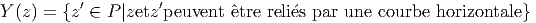
Soient Z1 et Z2, deux champs de vecteurs horizontaux et Ω la 2-forme de courbure associée à la connexion choisie. On démontre alors (théorème d’Ambrose-Singer) que les éléments de LieG qui sont de la forme Ωz(Z1(z),Z2(z)) engendrent l’algèbre de Lie du groupe d’holonomie au point z.
D’une certaine façon, le groupe d’holonomie en z fournit donc une estimation de la courbure en ce point. Ceci est d’ailleurs assez intuitif : si un transport par parallelisme le long d’une courbe fermée n’entraîne aucune “rotation” du repère, c’est que la région dans laquelle on se promène est assez plate …
Soit P = P(M,G), un espace fibré principal, H un sous-groupe de G et soit Q = Q(M,H) une réduction du fibré P. Nous savons qu’une telle réduction est associée au choix d’une section globale (que nous désignerons par Φ) dans le fibré en espaces homogènes E = E(M,G∕H) qui est associé à P via l’action à gauche de G sur G∕H. On rappelle que Q = p-1(Φ(M)) où p désigne la projection de P sur E = PmodH.
Soit maintenant ω une forme de connexion définissant une forme de connexion principale dans P. On dira que cette connexion est réductible et se réduit à Q si la restriction (au sens de la restriction des applications) de ω à Q définit une connexion principale dans le fibré Q. En particulier, ω, restreinte à Q doit être à valeurs dans l’algèbre de Lie du groupe H.
Au niveau des algèbres de Lie, nous pouvons écrire 𝔤 = 𝔥 ⊕ 𝔰 où 𝔤 et 𝔥 désignent respectivement les algèbres de Lie de G et de H, et où 𝔰 est un sous-espace vectoriel supplémentaire de 𝔥 dans 𝔤, espace vectoriel qui peut être identifié avec l’espace tangent à l’origine de S = G∕H. Supposer la connexion ω réductible revient à supposer qu’elle ne possède pas de composantes le long de l’espace vectoriel 𝔰.
Soit ω une forme de connexion quelconque dans le fibré P et ωQ sa restriction au sous-fibré Q. On peut toujours décomposer
Soit Ω = dω + 1 2[ω ∧ ω] la courbure de ω et ΩQ sa restriction à Q. Il vient immédiatement :
![1
ΩQ = ΩΦ + D θΦ + -[θΦ ∧ θΦ ]
2](source674x.png)
Cette décomposition de la forme de connexion ω et de la courbure correspondante Ω peut être effectuée chaque fois qu’on a une réduction du fibré P (chaque fois qu’on a une section globale Φ de PmodH). La forme de connexion elle-même n’est pas nécessairement réductible : en général θΦ≠0.
Citons trois exemples particulièrement importants de ce type de construction. Nous n’aurons pas le loisir de beaucoup les discuter plus avant mais nous les proposons néanmoins au lecteur, comme thèmes de réflexion.