1.4 Champs de vecteurs
1.4.1 Notions élémentaires et intuitives
Avant de donner une définition générale des vecteurs et champs de vecteurs,
définition qui pourrait sembler assez abstraite de prime abord, nous souhaitons
motiver quelque peu cette définition. Le lecteur est déjà supposé être familier de
la notion élémentaire de vecteur, à savoir une classe d’équivalence de
bi-points parallèles et de même sens, dans l’espace affine I Rn. Un champ de
vecteurs de I Rn, au sens élémentaire du terme, est donc une application
qui, à tout point de I Rn – considéré comme espace affine – associe un
vecteur de I Rn –considéré comme espace vectoriel. Intuitivement, on a
une “flèche” en tout point ; on peut penser à l’exemple du champ des
vitesses d’un solide en mouvement, mais on peut aussi penser au champ
magnétique en tout point de l’espace, etc. En physique – mais aussi, comme
nous allons le voir, en mathématiques – un vecteur peut être considéré
comme un “petit déplacement”. Soit M une variété différentiable, f
une fonction différentiable ainsi que P et Q deux points de M. Si M
était un espace affine (comme I Rn), cela aurait un sens de considérer la
différence de Q et de P, puisque cette différence définirait simplement le
vecteur 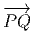 = Q - P. On pourrait aussi (mais on peut de toutes façons)
considérer la différence f(Q) - f(P) des valeurs prises par f en Q et
P. Dans le cas de M = I Rn et lorsque Q (coordonnées x′) tend vers P
(coordonnées x), le théorème des accroissement finis (ou celui de Taylor) nous dit
que
f(x′) - f(x) = (x′- x)i∂∕∂xif(x) + … = vi∂∕∂xif(x) + … où les nombres
vi = (x′-x)i ne sont autres que les composantes du vecteur
= Q - P. On pourrait aussi (mais on peut de toutes façons)
considérer la différence f(Q) - f(P) des valeurs prises par f en Q et
P. Dans le cas de M = I Rn et lorsque Q (coordonnées x′) tend vers P
(coordonnées x), le théorème des accroissement finis (ou celui de Taylor) nous dit
que
f(x′) - f(x) = (x′- x)i∂∕∂xif(x) + … = vi∂∕∂xif(x) + … où les nombres
vi = (x′-x)i ne sont autres que les composantes du vecteur 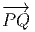 = Q-P dans le
repère où P et Q ont des composantes xi et x′i. Dans le cas des variétés,
l’expression (x′- x)i∂∕∂xif(x) a encore un sens. En effet, choisissons tout
d’abord une carte, et notons v la quantité v = vi∂∕∂xi. Si x(P) sont les
coordonnées de P dans le domaine de la carte x, on pourra considérer la
quantité
= Q-P dans le
repère où P et Q ont des composantes xi et x′i. Dans le cas des variétés,
l’expression (x′- x)i∂∕∂xif(x) a encore un sens. En effet, choisissons tout
d’abord une carte, et notons v la quantité v = vi∂∕∂xi. Si x(P) sont les
coordonnées de P dans le domaine de la carte x, on pourra considérer la
quantité
![|-----------------|
|v[f] = vi-∂if(x) |
----------∂x------](source4x.png) qui
nous décrit la variation - au premier ordre – de f dans ce que nous avons envie
d’appeler la direction v. La quantité précédente v[f] est elle-même une
fonction, qui, lorsqu’elle est évaluée au point P nous fournit un nombre
v[f](P).
qui
nous décrit la variation - au premier ordre – de f dans ce que nous avons envie
d’appeler la direction v. La quantité précédente v[f] est elle-même une
fonction, qui, lorsqu’elle est évaluée au point P nous fournit un nombre
v[f](P).
1.4.2 Vecteurs, espace tangent et champs de vecteurs
Dans le cas des variétés, il est clair que les vecteurs ne peuvent pas être définis
comme des bi-points (ou des classes d’équivalences de bi-points), par contre, rien ne
nous empêche d’utiliser leur propriété de machine-à-fabriquer-des-dérivées-partielles
pour les définir de façon générale. Dans le domaine d’une carte x, un champ de
vecteurs sera donc défini comme un opérateur de différentiation d’ordre 1 à
savoir
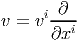 Cet
opérateur agit sur les fonctions f ∈ C∞(M) pour donner d’autres fonctions
(puisque v[f] ∈ C∞(M)). Le champ de vecteurs v ainsi défini est indépendant de
la carte choisie.
Cet
opérateur agit sur les fonctions f ∈ C∞(M) pour donner d’autres fonctions
(puisque v[f] ∈ C∞(M)). Le champ de vecteurs v ainsi défini est indépendant de
la carte choisie.
L’opérateur différentiel d’ordre 1 noté v = vi∂∕∂xi est un champ de vecteurs
car les vi sont des fonctions sur M alors que v(P) = vi(P)∂∕∂xi est un vecteur au
point P, de composantes vi(P).
En géométrie élémentaire des courbes, la tangente en P à une courbe
(différentiable) est définie comme limite des sécantes PQ lorsque Q tends vers
P ; cela signifie que les vecteurs 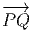 tendent vers un vecteur tangent à la courbe.
En géométrie des variétés différentiables, on pourrait faire de même, à
condition de plonger notre variété (par exemple la sphère usuelle S2) dans
un espace plus grand (par exemple I R3) et voir ainsi, un vecteur de S2
comme un vecteur tangent à la sphère (et donc “sortant” de celle-ci) ; mais
une telle contrainte serait précisément contraire à l’idée même du calcul
intrinsèque sur les variétés, calcul qui se veut, justement, indépendant de
l’existence de plongements possibles. La définition adoptée précédemment est
bien indépendante de la présence d’un espace affine ambiant, mais il est
néanmoins commode, pour l’intuition, de visualiser nos vecteurs de façon
élémentaire et d’adopter une terminologie qui nous rappelle des situations bien
connues. Pour ces raisons, un vecteur de la variété M en un point P est
souvent appelé vecteur tangent en P, l’ensemble de ces vecteurs se note
T(M,P) ou encore TP M et est désigné sous le nom de espace tangent à
M en P ; on a donc un espace tangent en chaque point de la variété.
L’ensemble des vecteurs eux-mêmes (tous les vecteurs), se note T(M) ou
simplement TM et est appelé l’espace tangent à M ou encore, pour une
raison qu’on expliquera ultérieurement le fibré tangent à M (“tangent
bundle”). Un élément de TM est donc la donnée (P,u) d’un point de M et
d’un vecteur en ce point. Attention, il faut bien distinguer les notions
de vecteur en un point et de champs de vecteurs (mais nous allons très
souvent oublier cette distinction). L’ensemble des champs de vecteurs se
note ΓTM. Notons que cet espace est un espace vectoriel (de dimension
infinie), et T(M,P) est un espace vectoriel de dimension n (supposant que
M est elle-même de dimension n), alors que TM n’est pas un espace
vectoriel du tout (on ne peut pas additionner un vecteur en P avec un
vecteur en Q !). On verra que TM, que l’on peut considérer comme une
collection d’espaces vectoriels paramètrisés par les points de M, possède la
structure d’espace fibré vectoriel (cette structure sera définie et étudiée plus
loin). Notons que l’espace TM est lui-même une variété différentiable.
Supposons que M soit une variété de dimension n, un point P de M est en
effet caractérisé (dans une certaine carte) par n composantes xμ et un
“point” (c’est à dire un élément) de TM consistera en la donnée d’un
couple (P,u) ∈ M × T(M,P) c’est à dire 2n nombres (n nombres xμ et n
composantes du vecteur u dans une base choisie de l’espace vectoriel T(M,P).
Ainsi TM est une variété de dimension 2n. Intuitivement, on peut se
représenter par exemple TS2 comme la donnée d’une infinité de plans
tangents collés à la sphère ; il s’agit, dans ce cas d’une variété de dimension
4.
tendent vers un vecteur tangent à la courbe.
En géométrie des variétés différentiables, on pourrait faire de même, à
condition de plonger notre variété (par exemple la sphère usuelle S2) dans
un espace plus grand (par exemple I R3) et voir ainsi, un vecteur de S2
comme un vecteur tangent à la sphère (et donc “sortant” de celle-ci) ; mais
une telle contrainte serait précisément contraire à l’idée même du calcul
intrinsèque sur les variétés, calcul qui se veut, justement, indépendant de
l’existence de plongements possibles. La définition adoptée précédemment est
bien indépendante de la présence d’un espace affine ambiant, mais il est
néanmoins commode, pour l’intuition, de visualiser nos vecteurs de façon
élémentaire et d’adopter une terminologie qui nous rappelle des situations bien
connues. Pour ces raisons, un vecteur de la variété M en un point P est
souvent appelé vecteur tangent en P, l’ensemble de ces vecteurs se note
T(M,P) ou encore TP M et est désigné sous le nom de espace tangent à
M en P ; on a donc un espace tangent en chaque point de la variété.
L’ensemble des vecteurs eux-mêmes (tous les vecteurs), se note T(M) ou
simplement TM et est appelé l’espace tangent à M ou encore, pour une
raison qu’on expliquera ultérieurement le fibré tangent à M (“tangent
bundle”). Un élément de TM est donc la donnée (P,u) d’un point de M et
d’un vecteur en ce point. Attention, il faut bien distinguer les notions
de vecteur en un point et de champs de vecteurs (mais nous allons très
souvent oublier cette distinction). L’ensemble des champs de vecteurs se
note ΓTM. Notons que cet espace est un espace vectoriel (de dimension
infinie), et T(M,P) est un espace vectoriel de dimension n (supposant que
M est elle-même de dimension n), alors que TM n’est pas un espace
vectoriel du tout (on ne peut pas additionner un vecteur en P avec un
vecteur en Q !). On verra que TM, que l’on peut considérer comme une
collection d’espaces vectoriels paramètrisés par les points de M, possède la
structure d’espace fibré vectoriel (cette structure sera définie et étudiée plus
loin). Notons que l’espace TM est lui-même une variété différentiable.
Supposons que M soit une variété de dimension n, un point P de M est en
effet caractérisé (dans une certaine carte) par n composantes xμ et un
“point” (c’est à dire un élément) de TM consistera en la donnée d’un
couple (P,u) ∈ M × T(M,P) c’est à dire 2n nombres (n nombres xμ et n
composantes du vecteur u dans une base choisie de l’espace vectoriel T(M,P).
Ainsi TM est une variété de dimension 2n. Intuitivement, on peut se
représenter par exemple TS2 comme la donnée d’une infinité de plans
tangents collés à la sphère ; il s’agit, dans ce cas d’une variété de dimension
4.
1.4.3 Règle de Leibniz
Soit v un champ de vecteurs. Il pourra donc s’écrire localement (c’est à dire dans
une certaine carte) v = vμ∂∕∂xμ. Si f et g désignent deux fonctions sur M, il est
clair que
![-∂-- --∂- --∂-
∂xμ[fg ] = ∂x μ[f]g + f∂x μ[g]](source7x.png) Par
conséquent on aura plus généralement :
Par
conséquent on aura plus généralement :
![|---------------------|
|v[fg] = v[f ]g + f v[g ]|
----------------------](source8x.png) On
retrouve la règle usuelle de dérivation d’un produit. De façon générale, si
On
retrouve la règle usuelle de dérivation d’un produit. De façon générale, si
 est une algèbre associative, on dit que v est une dérivation, lorsque
v est une application linéaire (un “opérateur”) de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈
est une algèbre associative, on dit que v est une dérivation, lorsque
v est une application linéaire (un “opérateur”) de A dans A telle que
v[fg] = v[f]g + fv[g] avec f,g ∈ . Les champs de vecteurs sont des
dérivations de l’algèbre associative (et commutative) C∞(M). On pourrait
d’ailleurs les définir directement par cette propriété. En d’autres termes,
ΓTM = DerC∞(M).
. Les champs de vecteurs sont des
dérivations de l’algèbre associative (et commutative) C∞(M). On pourrait
d’ailleurs les définir directement par cette propriété. En d’autres termes,
ΓTM = DerC∞(M).
1.4.4 Crochet de deux champs de vecteurs
Notons que le produit de deux vecteurs n’est pas un vecteur (produit
défini par composition de l’action des vecteurs sur les fonctions) mais
un opérateur différentiel d’ordre 2. En effet, soient v = vμ∂∕∂xμ
et w = wν∂∕∂xν deux champs de vecteurs (attention les vμ est les
wν n’ont aucune raison d’être constants dans la carte choisie). Alors,
(vw)[f] = v[w[f]] = v[wν∂∕∂xν[f]] = vμ∂∕∂xμ[wν∂∕∂xν[f]] = vμ∂∕∂xμ[wν]∂∕∂xν[f]+vμwν∂2∕∂xμ∂xν[f]
Par contre, le commutateur (notation crochet) de deux champs de vecteurs, défini
par
![|-----------------|
|[v, w] = vw - wv |
------------------](source9x.png) est
un champ de vecteurs. Pour s’en convaincre, il suffit de vérifier que c’est bien
un opérateur différentiel d’ordre un. Le petit calcul précédent montre
immédiatement que les dérivées secondes disparaissent lorsqu’on calcule la
différence et qu’il reste
est
un champ de vecteurs. Pour s’en convaincre, il suffit de vérifier que c’est bien
un opérateur différentiel d’ordre un. Le petit calcul précédent montre
immédiatement que les dérivées secondes disparaissent lorsqu’on calcule la
différence et qu’il reste
![[v, w][f ] = (vw )[f] - (wv )[f] = (v μ-∂-[w ν]-∂-- wμ--∂-[vν]-∂--)[f ]
∂xμ ∂xν ∂x μ ∂x ν](source10x.png) La
définition précédente du crochet [v,w] = vw - wv de deux champs de vecteurs
implique de façon immédiate les deux propriétés suivantes :
La
définition précédente du crochet [v,w] = vw - wv de deux champs de vecteurs
implique de façon immédiate les deux propriétés suivantes :
Antisymétrie
![|---------------|
-[u,v] =-- [v,u]|](source11x.png) Identité de Jacobi
Identité de Jacobi
![|-----------------------------------|
[u,[v,w ]] + [v,[w, u]] + [w,[u,v]] = 0
-------------------------------------](source12x.png) Une algèbre (évidemment non associative) où les éléments vérifient ces deux
identités est appelée une algèbre de Lie. Notons qu’une algèbre de Lie est, en
particulier, un espace vectoriel. Nous pouvons donc conclure ce paragraphe en
disant “l’ensemble des champs de vecteurs est une algèbre de Lie (de dimension
infinie)”.
Une algèbre (évidemment non associative) où les éléments vérifient ces deux
identités est appelée une algèbre de Lie. Notons qu’une algèbre de Lie est, en
particulier, un espace vectoriel. Nous pouvons donc conclure ce paragraphe en
disant “l’ensemble des champs de vecteurs est une algèbre de Lie (de dimension
infinie)”.
1.4.5 Repère naturel associé à une carte
On appelle repère sur U ⊂ M, la donnée, en chaque point P ∈ U, d’une base de
l’espace vectoriel tangent en P. Un repère est en général “local”, c’est à
dire qu’on n’essaye pas, ou qu’on ne peut pas choisir U = M. Si xμ(P)
désignent les composantes de P dans une carte locale (U,x), on a déjà vu
que des vecteurs quelconques en P ou dans un voisinage de P peuvent
se décomposer sur les vecteurs ∂∕∂xμ. En d’autres termes, l’ensemble
des
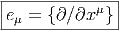 fournit un repère. Ce repère est appelé repère naturel associé à la carte x ou aux
coordonnées xμ (“coordinate frame”). Par suite de la propriété de commutativité
des dérivées partielles, il est évident que ∂2∕∂xμ∂xν - ∂2∕∂xν∂xμ = 0. En
d’autres termes, si {eμ} désigne le repère naturel associé à la carte xμ, on
a
fournit un repère. Ce repère est appelé repère naturel associé à la carte x ou aux
coordonnées xμ (“coordinate frame”). Par suite de la propriété de commutativité
des dérivées partielles, il est évident que ∂2∕∂xμ∂xν - ∂2∕∂xν∂xμ = 0. En
d’autres termes, si {eμ} désigne le repère naturel associé à la carte xμ, on
a
![[e ,e ] = 0
μ ν](source14x.png) Une telle propriété caractérise, en fait, les repères naturels.
Une telle propriété caractérise, en fait, les repères naturels.
1.4.6 Changement de carte
Soit P ∈ M → y(P) ∈ I Rn un nouveau système de coordonnées. Si x désigne
l’ancien système, on notera également y : I Rn I Rn les fonctions de changement
de carte, on écrira donc y(P) = y(x(P)). Le repère naturel associé aux
coordonnées x est eμ = {∂∕∂xμ}, celui associé aux coordonnées y est
eμ′ = {∂∕∂yμ}. Nous savons (depuis le secondaire) comment calculer la dérivée
d’une fonction composée, et donc
I Rn les fonctions de changement
de carte, on écrira donc y(P) = y(x(P)). Le repère naturel associé aux
coordonnées x est eμ = {∂∕∂xμ}, celui associé aux coordonnées y est
eμ′ = {∂∕∂yμ}. Nous savons (depuis le secondaire) comment calculer la dérivée
d’une fonction composée, et donc
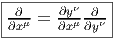 ce
qui, avec d’autres notations, s’écrit
ce
qui, avec d’autres notations, s’écrit
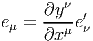 Notation
Notation
Il est souvent commode de noter tout simplement ∂μ les vecteurs du repère
naturel {eμ = ∂∕∂xμ} associés à la carte xμ. La décomposition d’un vecteur
quelconque v suivant ce repère s’écrit v = vμ∂
μ, où les vμ sont des nombres réels.
1.4.7 Repères mobiles (repères quelconques)
Dans un espace vectoriel, nous savons que les changements de base sont décrits
par des matrices “de passage” qui ne sont autres que des matrices inversibles Λαμ
quelconques. En géométrie différentielle, nous pouvons bien entendu faire de
même, à ceci près que la matrice Λαμ peut maintenant dépendre du point de la
variété. En d’autres termes, on a des matrices de passage dont les éléments sont
des fonctions sur la variété. Supposons que nous nous trouvons dans le domaine
d’une carte et que {∂μ} désigne le repère naturel associé. Ce repère, au point P,
constitue une base de l’espace tangent en P. Mais rien ne nous empêche de choisir
une autre base au même point. Si Λαμ désigne une matrice inversible
en P, alors la famille de vecteurs {eα = Λαμ∂
μ} est une autre base de
l’espace tangent TpM, c’est à dire un repère au point P. Un tel repère
est couramment désigné sous le nom de repère mobile. Notons qu’il n’y
a aucune raison, a priori, pour que ce repère coïncide avec le repère
naturellement associé à une autre carte que celle des xμ ; pour que cela soit le
cas, il faudrait qu’on puisse trouver une solution locale yα au système
d’équations ∂yα∕∂xμ = (Λ-1)
μα) où Λ-1 désigne la matrice inverse de la matrice
Λ. Le théorème garantissant l’existence de solutions pour une équation
différentielle aux dérivées partielles nous assure seulement l’existence d’une telle
solution yμ(xν)) le long d’une ligne, mais pas dans un voisinage ouvert de la
variété.
Soit {eα} un repère mobile. Nous avons déjà vu que le crochet (commutateur)
de deux champs de vecteurs est un champ de vecteurs. En particulier [eα,eβ] est
un champ de vecteurs qui, évalué au point P, appartient à l’espace tangent en ce
point et peut donc se décomposer sur une base de l’espace tangent en P. On
écrira donc
 = f αβ(P )eγ(P )](source18x.png) ou,
plus simplement
ou,
plus simplement
![|----------γ----|
-[eα,eβ-] =-fαβeγ-](source19x.png) où
les fαβγ sont des fonctions sur la variété qu’on appelle fonctions de structure du
repère mobile (on ne doit pas les appeler constantes de structure car, précisément,
elles ne sont pas constantes en général !).
où
les fαβγ sont des fonctions sur la variété qu’on appelle fonctions de structure du
repère mobile (on ne doit pas les appeler constantes de structure car, précisément,
elles ne sont pas constantes en général !).
Par ailleurs, on posera souvent ∂α = eα même s’il n’existe pas de système de
coordonnées {yα} tel que ∂
α soit le repère naturel associé. Le lecteur doit donc se
méfier de cet abus d’écriture pourtant commode : il est des cas où ∂α et ∂β ne
commutent pas !
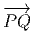 = Q - P. On pourrait aussi (mais on peut de toutes façons)
considérer la différence f(Q) - f(P) des valeurs prises par f en Q et
P. Dans le cas de M = I Rn et lorsque Q (coordonnées x′) tend vers P
(coordonnées x), le théorème des accroissement finis (ou celui de Taylor) nous dit
que 1
f(x′) - f(x) = (x′- x)i∂∕∂xif(x) + … = vi∂∕∂xif(x) + … où les nombres
vi = (x′-x)i ne sont autres que les composantes du vecteur
= Q - P. On pourrait aussi (mais on peut de toutes façons)
considérer la différence f(Q) - f(P) des valeurs prises par f en Q et
P. Dans le cas de M = I Rn et lorsque Q (coordonnées x′) tend vers P
(coordonnées x), le théorème des accroissement finis (ou celui de Taylor) nous dit
que 1
f(x′) - f(x) = (x′- x)i∂∕∂xif(x) + … = vi∂∕∂xif(x) + … où les nombres
vi = (x′-x)i ne sont autres que les composantes du vecteur 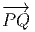 = Q-P dans le
repère où P et Q ont des composantes xi et x′i. Dans le cas des variétés,
l’expression (x′- x)i∂∕∂xif(x) a encore un sens. En effet, choisissons tout
d’abord une carte, et notons v la quantité v = vi∂∕∂xi. Si x(P) sont les
coordonnées de P dans le domaine de la carte x, on pourra considérer la
quantité
= Q-P dans le
repère où P et Q ont des composantes xi et x′i. Dans le cas des variétés,
l’expression (x′- x)i∂∕∂xif(x) a encore un sens. En effet, choisissons tout
d’abord une carte, et notons v la quantité v = vi∂∕∂xi. Si x(P) sont les
coordonnées de P dans le domaine de la carte x, on pourra considérer la
quantité
![|-----------------|
|v[f] = vi-∂if(x) |
----------∂x------](source4x.png)
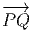 tendent vers un vecteur tangent à la courbe.
En géométrie des variétés différentiables, on pourrait faire de même, à
condition de plonger notre variété (par exemple la sphère usuelle
tendent vers un vecteur tangent à la courbe.
En géométrie des variétés différentiables, on pourrait faire de même, à
condition de plonger notre variété (par exemple la sphère usuelle ![-∂-- --∂- --∂-
∂xμ[fg ] = ∂x μ[f]g + f∂x μ[g]](source7x.png)
![|---------------------|
|v[fg] = v[f ]g + f v[g ]|
----------------------](source8x.png)

![|-----------------|
|[v, w] = vw - wv |
------------------](source9x.png)
![[v, w][f ] = (vw )[f] - (wv )[f] = (v μ-∂-[w ν]-∂-- wμ--∂-[vν]-∂--)[f ]
∂xμ ∂xν ∂x μ ∂x ν](source10x.png)
![|---------------|
-[u,v] =-- [v,u]|](source11x.png)
![|-----------------------------------|
[u,[v,w ]] + [v,[w, u]] + [w,[u,v]] = 0
-------------------------------------](source12x.png)
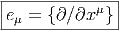
![[e ,e ] = 0
μ ν](source14x.png)
 I R
I R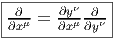
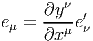
 = f αβ(P )eγ(P )](source18x.png)
![|----------γ----|
-[eα,eβ-] =-fαβeγ-](source19x.png)