[next] [prev] [prev-tail] [tail] [up]

1.8 Dérivées de Lie

La notion usuelle de dérivée d’une fonction numérique f nous permet de préciser la notion de variation locale de cette fonction lorsque son argument croît ou décroît. Lorsque l’argument se déplace sur une variété de dimension supérieure à 1, la variation ne sera définie que si on précise dans quelle direction se déplace le point (l’argument). En d’autres termes, la généralisation de la notion de dérivée invoque obligatoirement la notion de vecteur tangent. La dérivée d’une fonction f : M → I R par rapport à un champ de vecteurs X se note LXf et est tout simplement définie par l’égalité

LX f = df[X ] = X [f ]
Ainsi, la différentielle de f “code” toutes les variations possibles, alors que la dérivée de f dans la direction X est obtenue en évaluant la différentielle de f sur le vecteur X.

Cette notion de dérivée se généralise au cas où f n’est plus une fonction sur M à valeurs réelles mais un champ t de tenseurs quelconques (ou même, comme on le verra plus tard, une section d’un fibré quelconque au-dessus de M). On a envie de donner un sens à la limite de t(x+ϵX)-t(x) ϵ lorsque ϵ tend vers 0. La quantité correspondante se note toujours LXt et s’appelle dérivée de Lie du tenseur t par rapport au champ de vecteurs X. C’est un tenseur de même type que t. On veut que LX soit une dérivation de l’algèbre tensorielle, c’est-à-dire qu’on impose

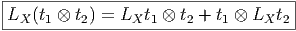
|-----------------------------------| LX-(t1 ⊗-t2)-=-LX-t1-⊗-t2 +-t1-⊗-LX-t2
où t1 et t2 sont des tenseurs quelconques. Pour définir complètement LX il suffit de préciser la valeur de LXY lorsque Y est un champ de vecteurs (contravariants) et de LXω lorsque ω est une 1-forme (champ de vecteurs covariants). Dans le premier cas on pose
LX Y = [X, Y]
Par exemple,
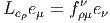
Le ρeμ = fνρμeν
Dans le second cas (action de L sur les 1-formes), on définit LXω par la relation
[LX ω ](Y ) = X (ω(Y )) - ω ([X, Y ])
où Y est, comme X, un champ de vecteurs sur M. Nous laissons le soin au lecteur de démontrer que cette définition, ainsi que la propriété de dérivation, conduit à la relation suivante caractérisant l’action de LX sur les formes différentielles :
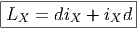
|----------------| |LX = diX + iX d| ------------------
Cette dernière propriété peut d’ailleurs servir de définition. Il est alors immédiat de vérifier que LX est une dérivation de l’algèbre des formes différentielles puisque d et iX sont des dérivations graduées. LX est une “vraie” dérivation et non une dérivation graduée : le signe (-1) potentiel, dans la règle de Leibniz, disparaît.
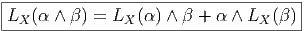
|-------------------------------------| -LX-(α-∧-β)-=-LX-(α)-∧-β-+-α-∧-LX-(β)-|
De plus LX ne modifie pas le degré des formes puisque d et iX agissent en sens contraires. La relation précédente conduit immédiatement à la formule explicite
k L ω (X ,...,X ) = X (ω (X ,...,X )) - ∑ ω (X ,...,[X, X ],...,X ) X 1 k 1 k 1 i k i=1

Le cas particulier où ω est une 1-forme se retrouve aussi aisément. Notons que, dans ce dernier cas, si eμ et eμ désignent deux repères duaux l’un de l’autre (un repère mobile et le co-repère mobile dual), on a

LX eμ = eμ([eν,X ])eν
et en particulier
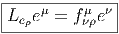
|-------------| Le ρeμ = fμνρeν| ---------------
En coordonnées locales, lorqu’on choisit un repère naturel, on peut écrire ω = 1∕k!ωμ1…μkdxμ1 ∧… ∧ dxμk et on obtient
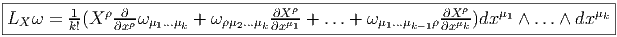
|--------1---ρ-∂------------------∂Xρ------------------∂Xρ----μ-----------μ--| -LX-ω-=-k!(X--∂xρωμ1...μk-+-ωρμ2...μk-∂xμ1-+-...+--ωμ1...μk-1ρ∂xμk)dx-1 ∧-...-∧-dx-k|

Dans le cas des formes, la définition de la dérivée de Lie implique immédiatement que LX commute avec d (car d2 = 0), ainsi qu’avec i X (puisque iviv = 0), et que, par ailleurs

i[X,Y] = LX iY - iYLX [LX ,LY ] = L [X,Y]

Enfin, si f est une application différentiable et ω une forme différentielle, on voit que

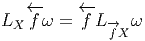
←- ←- LX f ω = f L-→fXω

Nous terminons ce paragraphe en montrant que la dérivée de Lie du tenseur de Kronecker δ = eμ ⊗ eμ est nulle dans toutes les directions. En effet

μ μ Leρδ = Le ρeμ ⊗ e + eμ ⊗ Le ρe μ μ ν = [eρ,eμ] ⊗ e + eμ ⊗ fνρe = f σeσ ⊗ eμ + f μeμ ⊗ eν = 0 ρμ νρ

[next] [prev] [prev-tail] [front] [up]