3.6 Groupe des automorphismes. Groupe de jauge
3.6.1 Remarque terminologique
Nous utiliserons souvent l’expression “repère en x” —sans mettre les
guillemets !— pour parler d’un point z de P = P(M,G) se projetant au point x,
même si le fibré considéré n’est pas un sous-fibré de l’espace des repères mais un
fibré principal quelconque au dessus de M, avec groupe de structure G. Le
contexte devrait suffire à préciser s’il s’agit d’un repère de l’“espace interne”
—comme disent les physiciens— c’est à dire un élément d’un fibré principal
quelconque non relié au fibré FM des repères linéaires, ou, au contraire, d’un
repère de l’“espace externe”, c’est à dire un élément de FM (ou de OFM, ou
d’un autre sous-fibré de FM).
3.6.2 Automorphismes verticaux d’un espace fibré principal (définition)
3.6.3 Ecriture locale des transformations de jauge
Soit Φ une transformation de jauge, z un élément de P et σ une section locale au
voisinage de x = π(z) ∈ M. Le repère Φ(σ(x)) étant dans la même fibre (au
même point !) que le repère mobile σ(x), il doit être possible d’atteindre le
premier à partir du second par l’action d’un élément approprié de G que
nous noterons g(x), puisque G est transitif sur les fibres. Cet élément
est donc défini par l’équation Φ(σ(x)) = σ(x)g(x) c’est à dire encore
par
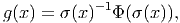 en
utilisant la notation introduite en fin de section 3.2.1. Notons que g(x) dépend
non seulement de Φ mais aussi de la section σ choisie ; on pourrait utiliser la
notation un peu lourde σg(x) pour désigner cet élément.
en
utilisant la notation introduite en fin de section 3.2.1. Notons que g(x) dépend
non seulement de Φ mais aussi de la section σ choisie ; on pourrait utiliser la
notation un peu lourde σg(x) pour désigner cet élément.
Lorsque P est trivial, on sait qu’il existe des sections globales. Soit σ une telle
section, alors, l’équation précédente définit une application de M dans G ;
réciproquement, la donnée d’une application g(x) de M dans G permet, lorsque le
fibré principal est trivial, de définir, via le choix d’une section globale σ, une
transformation de jauge Φ par la même équation. Lorsque P est trivial, on
peut donc identifier le groupe de jauge 𝔊 avec le groupe Ω0(M,G) des
applications différentiables de M dans G. La correspondance n’est cependant pas
canonique puisqu’elle dépend du choix d’une section globale σ. Cette
identification “explique” pourquoi les automorphismes verticaux sont désignés
par les physiciens (des particules) sous le nom de “transformations de
jauge locales”, le mot “local” se référant ici à la dépendance “en x” car
la transformation g(.) elle-même est globalement définie lorsque P est
trivial.
3.6.4 Deux autres définitions des transformations de jauge
- Soit Φ : P
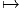 P une transformation de jauge. On sait que Φ(z) est
dans la même fibre que z, on doit donc pouvoir obtenir Φ(z) à partir
de z par action à droite d’un élément de G que nous désignerons par
ϕ(z) :
P une transformation de jauge. On sait que Φ(z) est
dans la même fibre que z, on doit donc pouvoir obtenir Φ(z) à partir
de z par action à droite d’un élément de G que nous désignerons par
ϕ(z) :
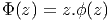 Nous obtenons donc ainsi une application ϕ de P dans G, mais
cette application n’est pas quelconque ; en effet, l’égalité Φ(zg) =
Φ(z)g peut s’écrire également zgϕ(zg) = zϕ(z)g et on obtient donc la
condition
Nous obtenons donc ainsi une application ϕ de P dans G, mais
cette application n’est pas quelconque ; en effet, l’égalité Φ(zg) =
Φ(z)g peut s’écrire également zgϕ(zg) = zϕ(z)g et on obtient donc la
condition
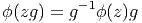 Il est évident que Φ et ϕ se déterminent l’un l’autre ; on peut
donc identifier le groupe de jauge 𝔊 avec l’ensemble ΩAd0(P,G) des
applications de P dans G qui sont équivariantes par l’action adjointe
de G.
Il est évident que Φ et ϕ se déterminent l’un l’autre ; on peut
donc identifier le groupe de jauge 𝔊 avec l’ensemble ΩAd0(P,G) des
applications de P dans G qui sont équivariantes par l’action adjointe
de G.
- La troisième définition de 𝔊 résulte en fait de la précédente et de
la discussion menée en section 3.3.10 (description 2). Soit, en effet
AdP = P×AdG le fibré adjoint, défini comme fibré en groupes, associé
à P grâce à l’action adjointe de G sur lui-même (voir section 3.3.6), les
éléments
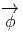 de AdP sont des classes d’équivalences z.k = zg.g-1kg et
les sections
de AdP sont des classes d’équivalences z.k = zg.g-1kg et
les sections 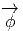 (x) de AdP peuvent donc s’identifier aux applications de
P dans G qui sont Ad-équivariantes. Ainsi, nous pouvons également
définir le groupe de jauge 𝔊 comme l’ensemble des sections du fibré
adjoint AdP.
(x) de AdP peuvent donc s’identifier aux applications de
P dans G qui sont Ad-équivariantes. Ainsi, nous pouvons également
définir le groupe de jauge 𝔊 comme l’ensemble des sections du fibré
adjoint AdP.
3.6.5 Automorphismes quelconques d’un espace fibré principal
Soit P = P(M,G) un fibré principal et 𝔊 son groupe d’automorphismes verticaux
(groupe de jauge). Nous allons à présent considérer des automorphismes plus
généraux que ceux considérés dans les sous-sections précédentes. Jusqu’à présent,
nos automorphismes étaient verticaux, en ce sens que l’image Φ(z) de z par Φ
était dans la même fibre que z. Nous allons garder les conditions 1 et 3 données
dans la définition du groupe de jauge (section 3.6.2) mais atténuer la deuxième
condition ; les automorphismes devront préserver les fibres au sens suivant :
l’image d’une fibre devra être une fibre, mais on n’imposera pas le fait qu’image
et antécédent appartiennent à la même fibre ! En d’autres termes, si
x désigne un point de M, l’ensemble Φ(π-1(x)), image de la fibre au
dessus de x par Φ doit être une fibre de P. Cette fibre image se projette
en un certain point y de M. L’action d’un tel automorphisme Φ définit
donc également une application de M dans M (à x on associe le point y
tel que y = π(Φ(π-1(x)))). Cette application est, par construction, un
difféomorphisme. On obtient donc de cette façon une projection du groupe AutP
des automorphismes de P (le groupe engendré par les automorphismes que nous
venons de définir) sur le groupe DiffM des difféomorphismes de M.
Deux automorphismes de P se projetant sur le même difféomorphisme de
M diffèrent manifestement (au sens de la composition des morphismes)
par un automorphisme ne changeant pas le point de base, c’est à dire
par un automorphisme vertical. Localement, ces “symétries de jauge”
(nom qu’on donne quelquefois aux éléments de AutP) sont donc codées à
l’aide d’un difféomorphisme de M et d’une transformation de jauge. Plus
précisément, on a la fibration principale 𝔊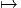 AutP
AutP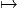 DiffM (noter que 𝔊
est un groupe de dimension infinie) qu’on peut représenter par la figure
3.19
DiffM (noter que 𝔊
est un groupe de dimension infinie) qu’on peut représenter par la figure
3.19
3.6.6 Action des automorphismes sur les espaces fibrés associés
- Soit E = P ×GF un espace fibré associé au fibré principal P =
P(M,G) obtenu à partir de l’action à gauche ρ de G sur F, z.f =
zg.ρ(g-1)f ∈ E. L’action à droite de G sur P n’existe plus au niveau
de E puisqu’on a fabriqué un espace quotient en divisant par cette
action. Par contre, on peut utiliser l’action à gauche de 𝔊 sur P pour
définir une action (à gauche) de
 sur n’importe quel fibré associé à
P. Ainsi,
sur n’importe quel fibré associé à
P. Ainsi,
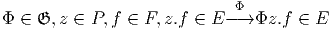
- 𝔊 agit non seulement sur E mais sur l’espace ΓE de ses sections. Soit
u ∈ ΓE, x ∈ M, u(x) ∈ E ;on définit
 = Φ (u (x))](source530x.png)
3.6.7 Le cas des espaces vectoriels (un cas trivial mais instructif !)
Un fibré vectoriel n’est autre, intuitivement, qu’une famille Ex d’espaces vectoriels
de même dimension, “collés” ensemble, et paramétrisés par une variété (x ∈ M).
Lorsque M se réduit à un seul point, on n’a qu’une seule fibre et donc un seul
espace vectoriel. On peut donc considérer un espace vectoriel E comme un
fibré vectoriel au dessus d’un point ! Ce fibré vectoriel particulièrement
trivial est associé à un fibré principal également constitué d’une seule
fibre, fibre qui n’est autre que l’ensemble P des bases de l’espace vectoriel
E. Si on suppose que E est isomorphe à I Rn, on voit que cette fibre est
difféomorphe au groupe GL(n, I R). Si on choisit une base σ = {σμ} de
référence (une section !), on obtient une correspondance bi-univoque
entre bases (éléments de P) et matrices inversibles (éléments du groupe
GL(n, I R)). L’identification de P avec GL(n, I R) dépend de la base σ choisie. Le
groupe matriciel GL(n, I R) agit sur P ; cette action ne dépend pas du
choix de σ. En effet, si e = (eμ) ∈ P et Λ = (Λνμ) ∈ GL(n, I R), on obtient
e′ = eΛ ∈ P via eν′ = eμΛνμ. Les vecteurs u de l’espace vectoriel E sont des
classes d’équivalence u = eμ.uμ avec e = {e
μ}∈ P et uμ ∈ I Rn, la relation
d’équivalence identifiant eμ.uμ avec e
νΛμν.(Λ-1)
ρμuρ. Le groupe GL(n, I R) n’agit
donc pas sur E (il n’agit que sur les composantes des vecteurs de E). Par
contre, l’espace vectoriel E possède un groupe d’automorphismes AutE (les
applications linéaires bijectives). Si u ∈ E et Φ ∈ AutE alors Φu ∈ E ; les
automorphismes Φ agissent aussi sur les bases e = {eμ}, l’action en question
résultant de l’action sur chacun des vecteurs de base. Il faut bien voir
que les groupes AutE et GL(n, I R) sont différents ! Cependant, si on
se choisit une base σ = σμ de référence, on peut, de façon élémentaire
—voir cours de Terminale de nos lycées— associer, à tout élément Φ de
AutE, une matrice Λ de GL(n, I R). Dans le cas d’un espace vectoriel,
donc, le groupe structural et le groupe des automorphismes (qui, dans ce
cas, sont nécessairement verticaux), bien que conceptuellement distincts,
sont identifiables dès qu’on se choisit une base de référence (c’est à dire
une section de ce fibré !). En particulier, lorsque E est de dimension
finie, ces deux groupes sont de dimension finie. Dès qu’on passe au cas
de fibrés vectoriels au dessus d’une variété M non réduite à un point,
l’identification n’est plus possible : G = GL(n, I R) reste ce qu’il était
mais 𝔊 = AutV P devient un groupe de dimension infinie qu’on peut se
représenter intuitivement comme une famille de groupe d’automorphismes
d’espaces vectoriels (les fibres de E) paramétrisés par les points de la base
M.
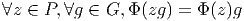
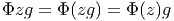
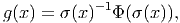
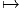
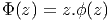
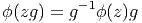
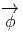 de
de 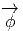 (
(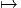
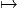

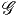
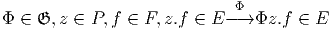
 = Φ (u (x))](source530x.png)